中科大&vivo最新深度估計DepthMaster:泛化能力、細節保留超越其他基于擴散方法
本文經3D視覺之心公眾號授權轉載,轉載請聯系出處。
單目深度估計的瓶頸
單目深度估計(Monocular Depth Estimation, MDE)因其簡單、低成本和易于部署的特點,受到了廣泛關注。與傳統的深度傳感技術(如LiDAR或立體視覺)不同,MDE僅需要一張RGB圖像作為輸入,因此在自動駕駛、虛擬現實和圖像合成等多個應用領域中具有很高的吸引力。然而,這也帶來了一個顯著的挑戰:如何在廣泛的應用場景中實現卓越的泛化能力,以有效應對場景布局、深度分布、光照條件等因素的多樣性和復雜性。這項任務并非易事,因為不同的場景和條件往往帶來非常大的變化。
近年來,零-shot單目深度估計主要發展為兩大類方法:基于數據的方法和基于模型的方法。基于數據的方法:依賴于大量的圖像-深度對,通過訓練得到圖像與深度之間的映射。然而,這一過程非常耗時且需要巨大的計算資源。與之相對,基于模型的方法則通過利用預訓練的骨干網絡,尤其是在穩定擴散模型(Stable Diffusion)上下文中,展現了較為高效的性能。例如,Marigold通過將深度估計重構為擴散去噪過程,在泛化和細節保留方面取得了令人印象深刻的成果。然而,迭代去噪過程導致了較低的推理速度。
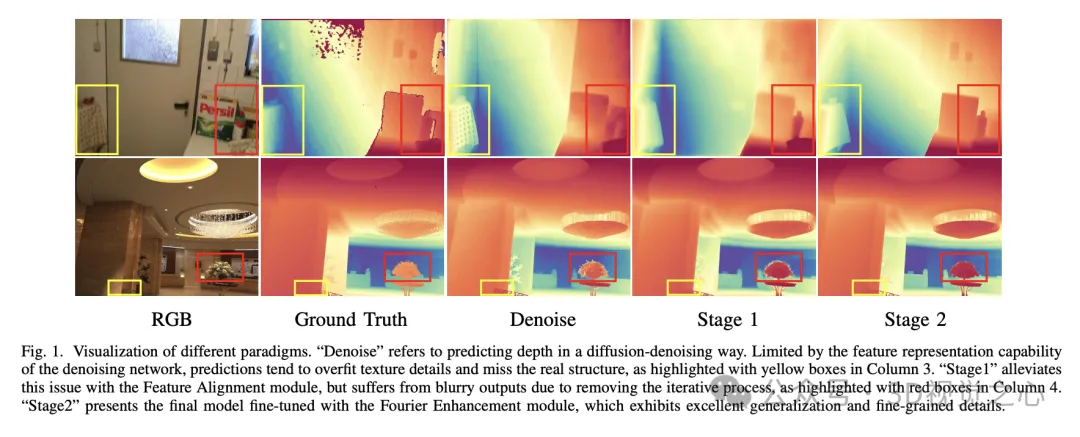
盡管擴散模型在單目深度估計中的應用取得了顯著的進展,但很少有研究深入探討如何最有效地將生成特征適應于判別性任務。因此,本文將重點分析擴散模型中的特征表示,特別是在如何優化去噪網絡的特征表示能力上。通常,擴散模型由圖像到潛在空間的編碼解碼器和去噪網絡組成。前者將圖像壓縮到潛在空間并重建,而后者則負責對場景進行感知與推理。通過實驗發現,主要的瓶頸在于去噪網絡的特征表示能力。事實上,用于預訓練去噪網絡的重建任務使得模型過于關注紋理細節,導致深度預測中的紋理不真實。因此,如何增強去噪網絡的特征表示能力并減少對無關細節的依賴,是將擴散模型應用于深度估計任務的關鍵問題。
DepthMaster【1】是一個定制的單步擴散模型,旨在提升深度估計模型的泛化能力和細節保留能力。
- 首先,我們引入了特征對齊模塊(Feature Alignment),通過高質量的外部視覺表示來提升去噪網絡的特征表示能力,并減少對紋理細節的過擬合。
- 其次,為了解決單步框架中缺乏細粒度細節的問題,我們提出了傅里葉增強模塊(Fourier Enhancement),在頻域內自適應平衡低頻結構特征和高頻細節特征,從而有效模擬擴散模型中多步去噪過程的學習。
通過這些優化,我們的方法在多種數據集上超越了其他基于擴散的深度估計方法,取得了最新的性能。
主要貢獻:
- 提出了DepthMaster,一種定制生成特征的創新方法,旨在將擴散模型適應于判別性深度估計任務。
- 引入了特征對齊模塊,以高質量的外部特征緩解對紋理細節的過擬合,并提出了傅里葉增強模塊,以在頻域內細化細粒度細節。
- 方法展現了最新的零樣本性能和卓越的細節保留能力,超越了其他基于擴散的算法,并在多個數據集上表現出色。
項目鏈接:https://indu1ge.github.io/DepthMaster_page/
具體方法

確定性范式

特征對齊模塊
穩定擴散v2由兩個主要組件組成:I2L編碼器-解碼器和去噪U-Net。I2L編碼器-解碼器負責特征壓縮,旨在減少推理時間和訓練成本。通過圖像重建訓練,它主要捕捉低層特征。與此不同,U-Net負責從噪聲圖像中恢復圖像,從而使其具備場景感知與推理能力。然而,由于U-Net是通過重建任務進行訓練的,它往往過度強調細節紋理,從而導致深度預測中的偽紋理問題(如圖1所示)。因此,我們引入語義正則化來增強U-Net的場景表示能力,并防止過度擬合低級的顏色信息。

傅里葉增強模塊
單步范式通過避免多步迭代過程和多次運行集成,有效地加速了推理過程。然而,擴散模型輸出的細粒度特征通常來自于迭代細化過程。因此,單步模型在處理時會出現模糊的預測(如圖1所示)。為了緩解這一問題,我們提出了傅里葉增強模塊,在頻域中進行操作,以增強高頻細節,從而有效模擬多步去噪過程中的學習。

加權多方向梯度損失

兩階段訓練策略
由于I2L編碼器-解碼器的深度重建精度已經足夠高,我們將重點微調U-Net。實驗表明,潛在空間的監督有助于模型更好地捕捉全局場景結構,而像素級的監督則有助于捕捉細粒度的細節,但也會引入全局結構的失真。基于這些觀察,我們提出了一個兩階段的訓練策略。

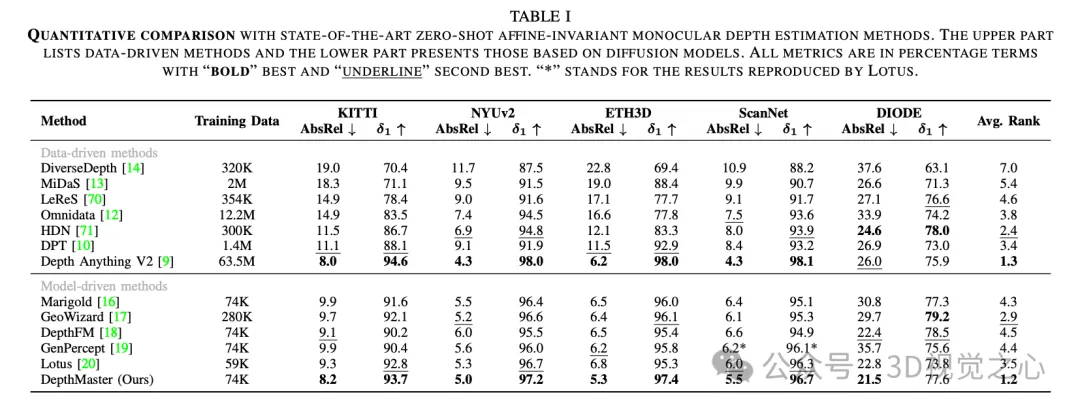
實驗效果
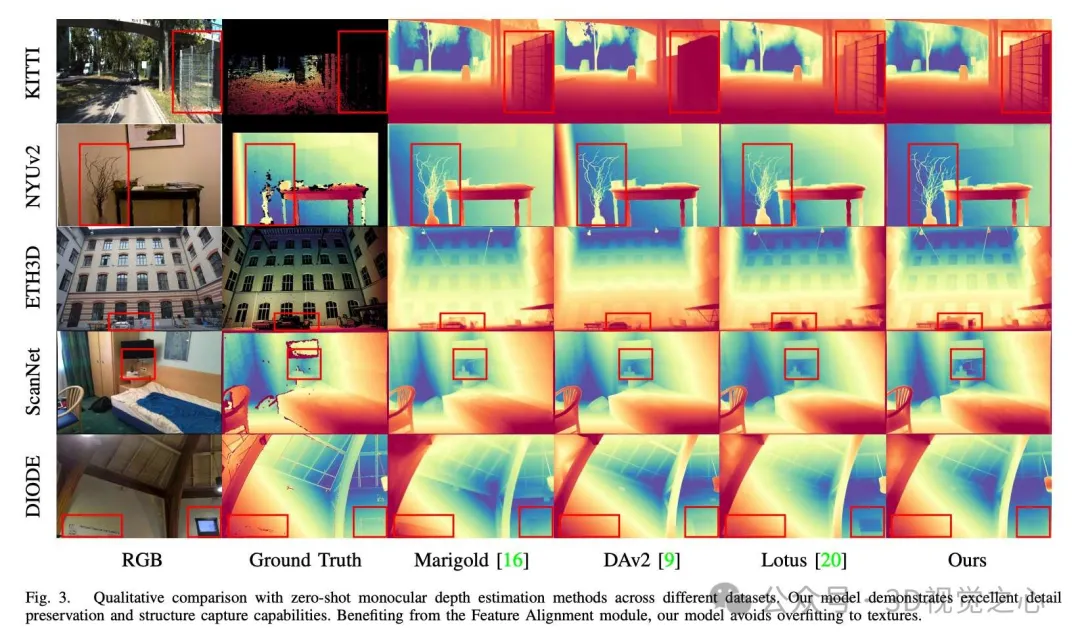

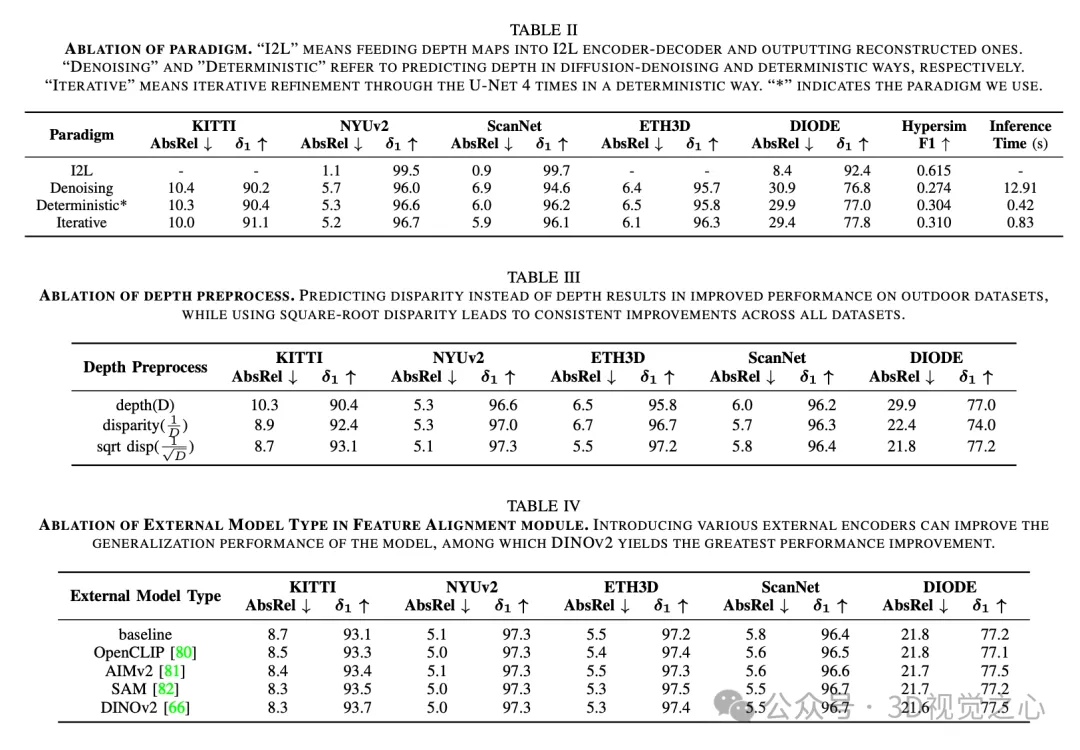
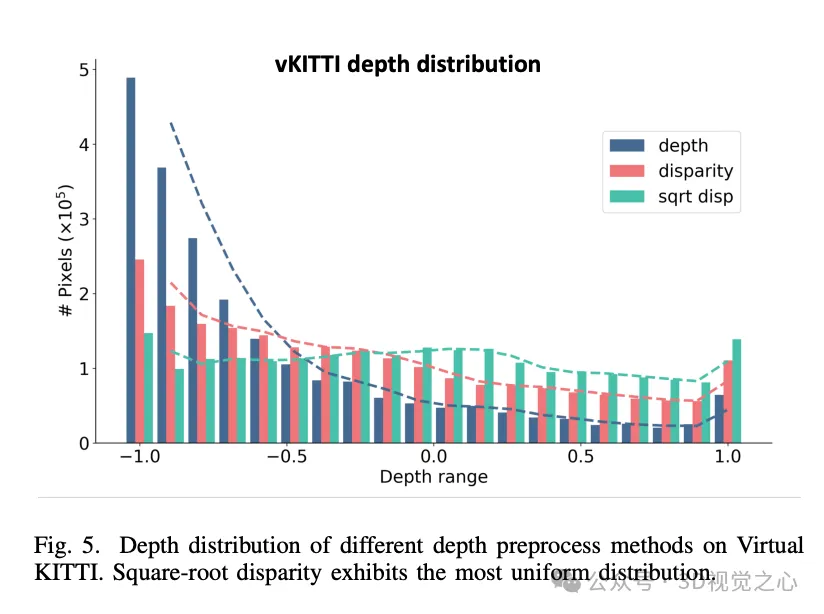
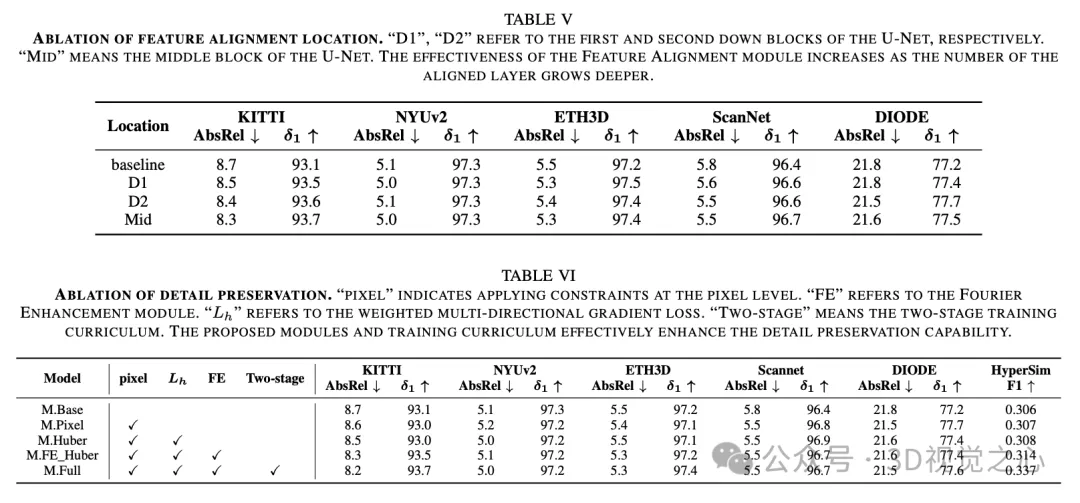
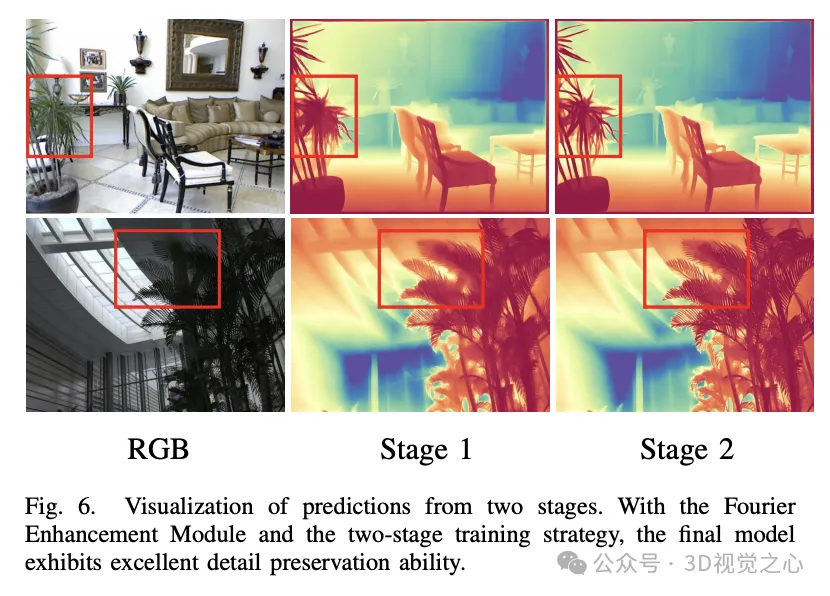
總結一下
DepthMaster是用于定制擴散模型以適應深度估計任務。通過引入特征對齊模塊,有效地緩解了對紋理細節的過擬合問題。此外,通過傅里葉增強模塊在頻域中操作,顯著增強了細粒度細節的保留能力。得益于這些精心設計,DepthMaster在零樣本性能和推理效率方面實現了顯著提升。廣泛的實驗驗證了我們方法的有效性,在泛化能力和細節保留方面達到了最新的水平,超越了其他基于擴散模型的方法,并在各種數據集上表現優異。