八個程序員都必須知道的常見數據結構
在軟件開發領域中,數據結構是我們能夠有效地組織、存儲和操作數據的基本構建塊。無論你是初學者還是經驗豐富的開發人員,掌握常見的數據結構對于編寫高效且優化代碼都至關重要。
在今天的文章中,我們將探討每個程序員都應該熟悉的8種基本數據結構,并提供清晰的解釋和相關示例,以幫助你了解它們的重要性和應用。
1. 數組:多功能主力
什么是數組?
數組可能是編程中最基本、使用最廣泛的數據結構。將數組視為存儲在連續內存位置的項目集合。它就像學校里一排儲物柜,每個儲物柜(元素)按順序編號,可容納一個物品。

數組如何工作?
數組基于索引的訪問原理工作。數組中的每個元素都與一個索引相關聯,通常從 0 開始。這樣可以快速直接地訪問數組中的任何元素。
示例:書架類比
假設你有一個書架,上面有 5 個插槽,編號為 0 到 4。每個插槽可以容納一本書。這類似于大小為 5 的數組。
# Creating an array (bookshelf) in Python
bookshelf = ["Harry Potter", "Lord of the Rings", "Pride and Prejudice", "1984", "To Kill a Mockingbird"]
# Accessing elements
print(bookshelf[0]) # Output: Harry Potter
print(bookshelf[2]) # Output: Pride and Prejudice
# Modifying an element
bookshelf[1] = "The Hobbit"
print(bookshelf) # Output: ['Harry Potter', 'The Hobbit', 'Pride and Prejudice', '1984', 'To Kill a Mockingbird']數組的優點
- 快速訪問:元素可以使用其索引立即訪問。
- 空間效率:數組使用連續的內存塊,因此內存效率高。
- 簡單:易于理解和使用。
數組的局限性
- 固定大小:在許多語言中,數組具有固定大小,創建后無法更改。
- 插入和刪除:這些操作可能很昂貴,尤其是對于大型數組。
實際應用
- 存儲和操作圖像像素數據
- 實現用于科學計算的矩陣
- 管理用戶界面中的項目列表
2. 鏈表:靈活的鏈
什么是鏈表?
鏈表是一種線性數據結構,其中元素存儲在節點中。每個節點包含一個數據字段和對序列中下一個節點的引用(或鏈接)。與數組不同,鏈表不會將元素存儲在連續的內存位置中。
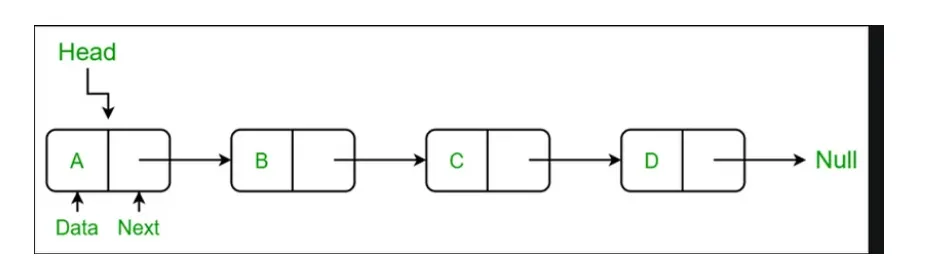
鏈表如何工作?
鏈表通過指針連接節點來工作。每個節點都知道序列中的下一個節點,從而形成鏈式結構。這允許在列表中的任何位置高效地插入和刪除元素。
示例:火車類比
將鏈表想象成一列火車。每節火車車廂(節點)都載有一些貨物(數據)并與下一節車廂相連。你可以輕松地在火車的任何位置添加或刪除車廂。
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def append(self, data):
new_node = Node(data)
if not self.head:
self.head = new_node
return
last_node = self.head
while last_node.next:
last_node = last_node.next
last_node.next = new_node
def display(self):
current = self.head
while current:
print(current.data, end=" -> ")
current = current.next
print("None")
# Creating a linked list
train = LinkedList()
train.append("Engine")
train.append("Passenger Car")
train.append("Dining Car")
train.append("Cargo Car")
train.display() # Output: Engine -> Passenger Car -> Dining Car -> Cargo Car -> None鏈表的優點
- 動態大小:鏈表在執行過程中可以增大或縮小大小。
- 插入和刪除效率高:添加或刪除元素速度很快,尤其是在列表的開頭。
- 靈活的內存分配:節點可以存儲在內存中的任何位置。
鏈表的局限性
- 順序訪問:要到達第 n 個元素,你需要從頭開始遍歷。
- 額外內存:每個節點都需要額外的內存來存儲對下一個節點的引用。
實際應用
- 在應用程序中實現撤消功能
- 管理音樂播放列表(可以輕松添加或刪除歌曲)
- 實現哈希表以解決沖突
3. 堆棧:后進先出冠軍
什么是堆棧?
堆棧是一種遵循后進先出 (LIFO) 原則的線性數據結構。可以將其視為一疊盤子:您只能從頂部添加或移除盤子。
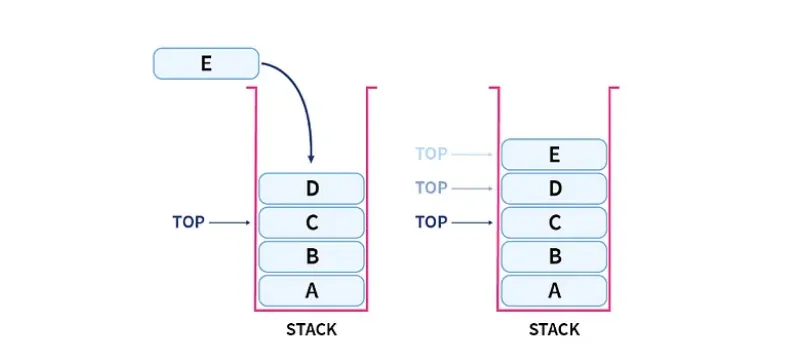
堆棧如何工作?
堆棧通過兩個主要操作進行操作:
- 推送:將元素添加到堆棧頂部。
- 彈出:從堆棧中刪除頂部元素。
示例:瀏覽器歷史記錄類比
你的 Web 瀏覽器的后退按鈕功能是堆棧的完美現實示例。當你訪問新頁面時,它們會被推送到堆棧上。當你點擊后退按鈕時,你會將頁面從堆棧中彈出。
class BrowserHistory:
def __init__(self):
self.history = []
def visit(self, url):
self.history.append(url)
print(f"Visited: {url}")
def back(self):
if len(self.history) > 1:
self.history.pop()
print(f"Went back to: {self.history[-1]}")
else:
print("Can't go back further!")
# Using our browser history stack
browser = BrowserHistory()
browser.visit("google.com")
browser.visit("youtube.com")
browser.visit("github.com")
browser.back()
browser.back()
browser.back()
browser.back()
# Output:
# Visited: google.com
# Visited: youtube.com
# Visited: github.com
# Went back to: youtube.com
# Went back to: google.com
# Can't go back further!堆棧的優點
- 簡單高效:堆棧操作簡單快捷。
- 內存管理:可用于管理函數調用和遞歸。
- 撤消機制:輕松在應用程序中實現撤消功能。
堆棧的局限性
- 訪問受限:任何時候都只能訪問頂部元素。
- 固定大小(在某些實現中):可能有最大大小限制。
實際應用
- 編程語言中的函數調用管理
- 表達式求值和語法解析
- 文本編輯器中的撤消-重做功能
4. 隊列:先進先出組織者
什么是隊列?
隊列是一種遵循先進先出 (FIFO) 原則的線性數據結構。這就像一隊人在等公共汽車:排在隊伍第一個的人就是第一個上車的人。
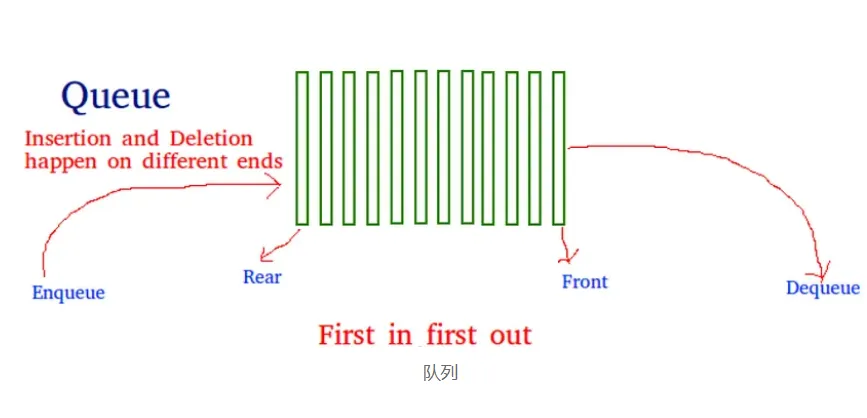
隊列如何工作?
隊列主要通過兩個操作進行操作:
- 入隊:將元素添加到隊列后面。
- 出隊:從隊列中刪除前面的元素。
示例:打印隊列類比
打印機隊列是隊列運行的經典示例。打印作業按接收順序進行處理。
from collections import deque
class PrinterQueue:
def __init__(self):
self.queue = deque()
def add_job(self, document):
self.queue.append(document)
print(f"Added '{document}' to the print queue")
def print_job(self):
if self.queue:
document = self.queue.popleft()
print(f"Printing: {document}")
else:
print("No jobs in the queue")
def display_queue(self):
print("Current queue:", list(self.queue))
# Using our printer queue
printer = PrinterQueue()
printer.add_job("Annual Report")
printer.add_job("Meeting Minutes")
printer.add_job("Employee Handbook")
printer.display_queue()
printer.print_job()
printer.print_job()
printer.display_queue()
# Output:
# Added 'Annual Report' to the print queue
# Added 'Meeting Minutes' to the print queue
# Added 'Employee Handbook' to the print queue
# Current queue: ['Annual Report', 'Meeting Minutes', 'Employee Handbook']
# Printing: Annual Report
# Printing: Meeting Minutes
# Current queue: ['Employee Handbook']隊列的優點
- 公平性:確保先到先得的處理。
- 可預測性:元素按已知順序處理。
- 解耦:適用于管理進程之間的異步數據傳輸。
隊列的局限性
- 訪問受限:只有前部和后部元素易于訪問。
- 可能出現瓶頸:如果入隊操作比出隊操作快,則隊列可以無限增長。
實際應用
- 操作系統中的任務調度
- 處理 Web 服務器中的請求
- 圖遍歷中的廣度優先搜索算法
5. 哈希表:閃電般快速的查找大師
什么是哈希表?
哈希表,也稱為哈希映射,是存儲鍵值對并提供快速數據檢索的數據結構。它們使用哈希函數計算存儲桶數組的索引,從中可以找到所需的值。
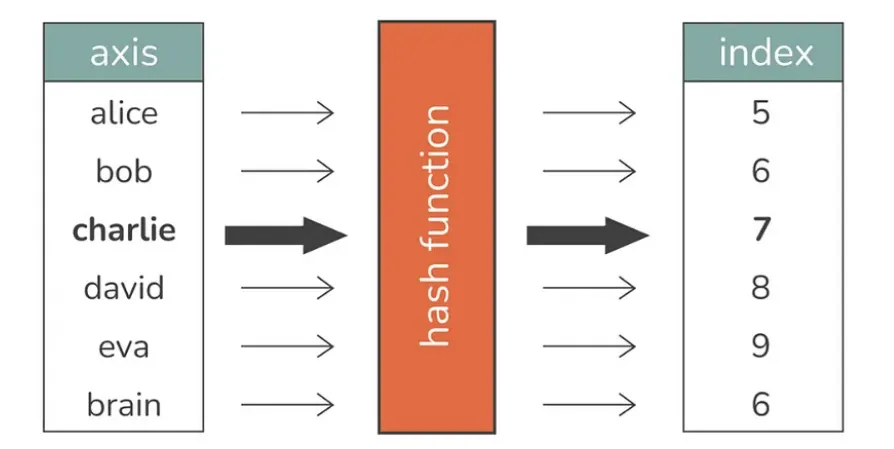
哈希表如何工作?
- 哈希函數將鍵作為輸入并生成索引。
- 鍵值對存儲在與此索引對應的存儲桶中。
- 要檢索值,需要再次對鍵進行哈希處理以找到正確的存儲桶。
示例:圖書館目錄類比
想象一個圖書館,其中書籍(值)根據從書名派生的唯一代碼(鍵)存儲在書架(存儲桶)中。此代碼由特殊公式(哈希函數)生成。
class SimpleHashTable:
def __init__(self, size):
self.size = size
self.table = [[] for _ in range(self.size)]
def _hash(self, key):
return sum(ord(char) for char in key) % self.size
def insert(self, key, value):
index = self._hash(key)
for item in self.table[index]:
if item[0] == key:
item[1] = value
return
self.table[index].append([key, value])
def get(self, key):
index = self._hash(key)
for item in self.table[index]:
if item[0] == key:
return item[1]
raise KeyError(key)
def display(self):
for i, bucket in enumerate(self.table):
print(f"Bucket {i}: {bucket}")
# Using our simple hash table
library = SimpleHashTable(10)
library.insert("Moby Dick", "Shelf A")
library.insert("Pride and Prejudice", "Shelf B")
library.insert("The Great Gatsby", "Shelf C")
library.insert("To Kill a Mockingbird", "Shelf D")
library.display()
print("Location of 'The Great Gatsby':", library.get("The Great Gatsby"))
# Output might look like:
# Bucket 0: []
# Bucket 1: []
# Bucket 2: [['Moby Dick', 'Shelf A']]
# Bucket 3: []
# Bucket 4: [['Pride and Prejudice', 'Shelf B']]
# Bucket 5: [['The Great Gatsby', 'Shelf C']]
# Bucket 6: []
# Bucket 7: [['To Kill a Mockingbird', 'Shelf D']]
# Bucket 8: []
# Bucket 9: []
# Location of 'The Great Gatsby': Shelf C哈希表的優點
- 快速查找:插入、刪除和搜索的平均時間復雜度為 O(1)。
- 靈活的鍵:可以使用各種數據類型作為鍵,而不僅僅是整數。
- 空間效率:可以有效地表示稀疏數據。
哈希表的局限性
- 沖突:不同的鍵可能會散列到同一個索引,需要解決沖突。
- 無序:不保持插入順序。
- 調整大小:隨著它們的增長可能需要調整大小,這可能會很昂貴。
實際應用
- 用編程語言實現字典
- 數據庫索引以實現更快的查詢
- Web 應用程序中的緩存機制
6. 樹:分層組織者
什么是樹?
樹是由通過邊連接的節點組成的分層數據結構。它們從根節點開始,然后分支到子節點,形成類似于倒置樹的結構。
樹如何工作?
樹以父子關系組織數據。每個節點可以有多個子節點,但只能有一個父節點(根節點除外)。此結構允許高效搜索和組織分層數據。
示例:家譜類比
家譜是樹形數據結構在現實世界中的完美示例。每個人都是一個節點,上面是父母,下面是孩子。
class FamilyMember:
def __init__(self, name):
self.name = name
self.children = []
def add_child(self, child):
self.children.append(child)
def display(self, level=0):
print(" " * level + self.name)
for child in self.children:
child.display(level + 1)
# Creating a family tree
grandparent = FamilyMember("Grandparent")
parent1 = FamilyMember("Parent 1")
parent2 = FamilyMember("Parent 2")
child1 = FamilyMember("Child 1")
child2 = FamilyMember("Child 2")
grandchild1 = FamilyMember("Grandchild 1")
grandparent.add_child(parent1)
grandparent.add_child(parent2)
parent1.add_child(child1)
parent1.add_child(child2)
child1.add_child(grandchild1)
# Displaying the family tree
grandparent.display()
# Output:
# Grandparent
# Parent 1
# Child 1
# Grandchild 1
# Child 2
# Parent 2樹的優點
- 層次表示:非常適合表示層次關系。
- 高效搜索:支持快速搜索操作,尤其是在平衡樹中。
- 靈活的結構:可用于實現其他數據結構,如堆和集合。
樹的局限性
- 復雜性:樹操作的實現和維護可能很復雜。
- 內存使用:可能比線性數據結構占用更多內存。
實際應用
- 操作系統中的文件系統
- Web 瀏覽器中的 HTML DOM(文檔對象模型)
- AI 決策樹和游戲樹
7. 圖:關系映射器
什么是圖?
圖是多功能數據結構,表示一組對象(頂點或節點),其中一些對象對通過鏈接(邊)連接。它們是建模復雜關系和網絡的理想選擇。
圖如何工作?
圖由頂點(節點)和邊(節點之間的連接)組成。邊可以是有向的(單向)或無向的(雙向)。可以使用鄰接矩陣或鄰接列表來實現圖形。
示例:社交網絡類比
社交網絡是現實世界中圖形的完美示例。每個人都是一個頂點,友誼是連接這些頂點的邊。
class SocialNetwork:
def __init__(self):
self.network = {}
def add_person(self, name):
if name not in self.network:
self.network[name] = set()
def add_friendship(self, person1, person2):
self.add_person(person1)
self.add_person(person2)
self.network[person1].add(person2)
self.network[person2].add(person1)
def display_network(self):
for person, friends in self.network.items():
print(f"{person}: {', '.join(friends)}")
# Creating a social network
social_net = SocialNetwork()
social_net.add_friendship("Alice", "Bob")
social_net.add_friendship("Alice", "Charlie")
social_net.add_friendship("Bob", "David")
social_net.add_friendship("Charlie", "David")
social_net.add_friendship("Eve", "Alice")
social_net.display_network()
# Output:
# Alice: Bob, Charlie, Eve
# Bob: Alice, David
# Charlie: Alice, David
# David: Bob, Charlie
# Eve: Alice圖形的優勢
- 關系建模:非常適合表示復雜的關系和連接。
- 多功能性:可以模擬各種各樣的現實場景。
- 強大的算法:存在許多用于解決復雜問題的圖形算法。
圖形的局限性
- 復雜性:對于大型數據集,實現和管理可能很復雜。
- 內存密集型:存儲連接可能需要大量內存。
- 遍歷挑戰:某些圖形問題的計算成本很高。
現實世界的應用
- 社交網絡分析
- GPS 和地圖系統
- 網絡路由協議
- 推薦系統
8. 堆:高效的優先級管理器
什么是堆?
堆是滿足堆屬性的專用樹型數據結構。在最大堆中,對于任何給定節點,節點的值大于或等于其子節點的值。在最小堆中,節點的值小于或等于其子節點的值。
堆如何工作?
堆保持元素的部分排序。它們提供對最大(對于最大堆)或最小(對于最小堆)元素的有效訪問,使其成為優先級隊列實現的理想選擇。
示例:急診室分診類比
想象一個急診室,根據患者病情的嚴重程度對其進行治療。該系統可以使用最大堆進行建模,其中優先級最高(病情最嚴重)的患者始終位于最頂部。
import heapq
class EmergencyRoom:
def __init__(self):
self.patients = []
self.patient_count = 0
def add_patient(self, name, priority):
# We use negative priority for max heap behavior
heapq.heappush(self.patients, (-priority, self.patient_count, name))
self.patient_count += 1
print(f"Patient {name} added with priority {priority}")
def treat_next_patient(self):
if self.patients:
_, _, name = heapq.heappop(self.patients)
print(f"Treating patient: {name}")
else:
print("No patients in waiting.")
def display_queue(self):
print("Current queue (Higher number means higher priority):")
sorted_patients = sorted(self.patients)
for priority, _, name in sorted_patients:
print(f" {name}: Priority {-priority}")
# Using our emergency room
er = EmergencyRoom()
er.add_patient("John", 3)
er.add_patient("Alice", 5)
er.add_patient("Bob", 1)
er.add_patient("Eve", 4)
er.display_queue()
er.treat_next_patient()
er.treat_next_patient()
er.display_queue()
# Output:
# Patient John added with priority 3
# Patient Alice added with priority 5
# Patient Bob added with priority 1
# Patient Eve added with priority 4
# Current queue (Higher number means higher priority):
# Alice: Priority 5
# Eve: Priority 4
# John: Priority 3
# Bob: Priority 1
# Treating patient: Alice
# Treating patient: Eve
# Current queue (Higher number means higher priority):
# John: Priority 3
# Bob: Priority 1堆的優點
- 高效的優先級管理:快速訪問最高(或最低)優先級元素。
- 快速插入:插入的時間復雜度為 O(log n)。
- 空間效率:可以高效地實現為數組。
堆的局限性
- 訪問受限:只有頂部元素易于訪問。
- 不適合搜索:搜索特定元素可能效率低下。
- 實現復雜:在操作期間維護堆屬性可能很棘手。
實際應用
- 操作系統中的任務調度程序
- 數據壓縮中的哈夫曼編碼
- 用于在圖中查找最短路徑的 Dijkstra 算法
- 編程語言中的內存管理
結論
對于任何希望編寫高效且優化的代碼的程序員來說,了解這8個基本數據結構都至關重要。每個結構都有自己的優點和缺點,使其適用于不同的場景:
- 數組擅長隨機訪問,非常適合大小已知且固定的場景。
- 鏈表在需要頻繁插入和刪除的情況下大放異彩。
- 堆棧非常適合管理函數調用和實現撤消機制。
- 隊列非常適合以先到先得的原則管理任務。
- 哈希表提供閃電般的快速查找,非常適合實現字典和緩存。
- 樹非常適合表示分層數據并實現高效搜索。
- 圖形在建模復雜關系和網絡方面無與倫比。
- 堆是優先級隊列實現和某些排序算法的首選結構。
通過掌握這些數據結構,你將能夠更好地選擇合適的工具來完成工作,從而為各種編程挑戰提供更高效、更優雅的解決方案。
請記住,成為一名熟練程序員的關鍵不僅在于了解這些結構,還在于了解何時以及如何在代碼中有效地應用它們。
在繼續編程之旅時,練習從頭開始實現這些數據結構并在各種場景中使用它們。這種實踐經驗可以加深你對它們的理解,并幫助你培養在不同情況下使用哪種結構的直覺。