以神經網絡為基礎的深度學習技術已經在諸多應用領域取得了有效成果。在實踐中，網絡架構可以顯著影響學習效率，一個好的神經網絡架構能夠融入問題的先驗知識，穩定網絡訓練，提高計算效率。目前，經典的網絡架構設計方法包括人工設計、神經網絡架構搜索（NAS）[1]、以及基于優化的網絡設計方法 [2]。人工設計的網絡架構如 ResNet 等；神經網絡架構搜索則通過搜索或強化學習的方式在搜索空間中尋找最佳網絡結構；基于優化的設計方法中的一種主流范式是算法展開（algorithm unrolling），該方法通常在有顯式目標函數的情況下，從優化算法的角度設計網絡結構。

然而，現有經典神經網絡架構設計大多忽略了網絡的萬有逼近性質 —— 這是神經網絡具備強大性能的關鍵因素之一。因此，這些設計方法在一定程度上失去了網絡的先驗性能保障。盡管兩層神經網絡在寬度趨于無窮的時候就已具有萬有逼近性質 [3]，在實際中，我們通常只能考慮有限寬的網絡結構，而這方面的表示分析的結果十分有限。實際上，無論是啟發性的人工設計，還是黑箱性質的神經網絡架構搜索，都很難在網絡設計中考慮萬有逼近性質。基于優化的神經網絡設計雖然相對更具解釋性，但其通常需要一個顯式的目標函數，這使得設計的網絡結構種類有限，限制了其應用范圍。如何系統性地設計具有萬有逼近性質的神經網絡架構，仍是一個重要的問題。

為了解決這個問題，北京大學林宙辰教授團隊提出了一種易于操作的基于優化算法設計具有萬有逼近性質保障的神經網絡架構的方法，其通過將基于梯度的一階優化算法的梯度項映射為具有一定性質的神經網絡模塊，再根據實際應用問題對模塊結構進行調整，就可以系統性地設計具有萬有逼近性質的神經網絡架構，并且可以與現有大多數基于模塊的網絡設計的方法無縫結合。論文還通過分析神經網絡微分方程（NODE）的逼近性質首次證明了具有一般跨層連接的神經網絡的萬有逼近性質，并利用提出的框架設計了 ConvNext、ViT 的變種網絡，取得了超越 baseline 的結果。論文被人工智能頂刊 TPAMI 接收。

• 論文：Designing Universally-Approximating Deep Neural Networks: A First-Order Optimization Approach
• 論文地址：https://ieeexplore.ieee.org/document/10477580

方法簡介

傳統的基于優化的神經網絡設計方法通常從一個具有顯式表示的目標函數出發，采用特定的優化算法進行求解，再將優化迭代格式映射為神經網絡架構，例如著名的 LISTA-NN 就是利用 LISTA 算法求解 LASSO 問題所得 [4]，這種方法受限于目標函數的顯式表達式，可設計得到的網絡結構有限。一些研究者嘗試通過自定義目標函數，再利用算法展開等方法設計網絡結構，但他們也需要如權重綁定等與實際情況可能不符的假設。

論文提出的易于操作的網絡架構設計方法從一階優化算法的更新格式出發，將梯度或鄰近點算法寫成如下的更新格式：

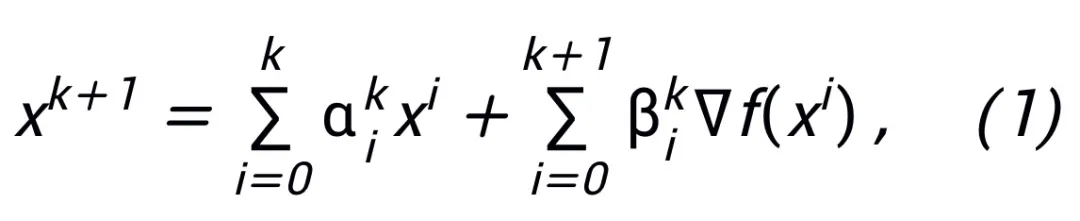
其中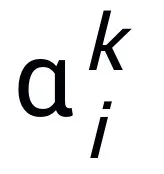、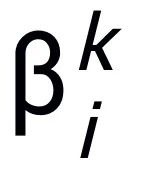表示第 k 步更新時的（步長）系數，再將梯度項替換為神經網絡中的可學習模塊 T，即可得到 L 層神經網絡的骨架：

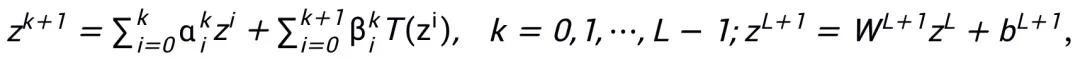
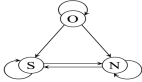
整體方法框架見圖 1。

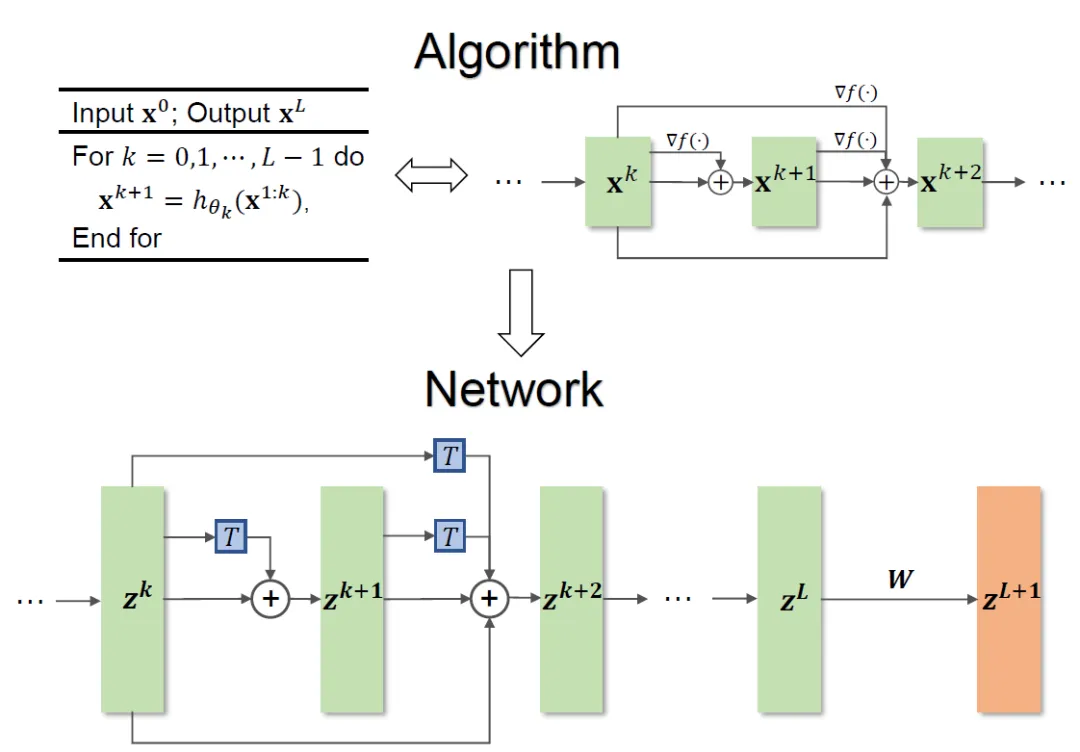
圖 1 網絡設計圖示

論文提出的方法可以啟發設計 ResNet、DenseNet 等經典網絡，并且解決了傳統基于優化設計網絡架構的方法局限于特定目標函數的問題。

模塊選取與架構細節

該方法所設計的網絡模塊 T 只要求有包含兩層網絡結構，即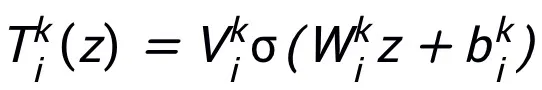，作為其子結構，即可保證所設計的網絡具有萬有逼近性質，其中所表達的層的寬度是有限的（即不隨逼近精度的提高而增長），整個網絡的萬有逼近性質不是靠加寬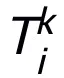的層來獲得的。模塊 T 可以是 ResNet 中廣泛運用的 pre-activation 塊，也可以是 Transformer 中的注意力 + 前饋層的結構。T 中的激活函數可以是 ReLU、GeLU、Sigmoid 等常用激活函數。還可以根據具體任務在中添加對應的歸一化層。另外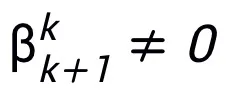，時，設計的網絡是隱式網絡 [5]，可以用不動點迭代的方法逼近隱格式，或采用隱式微分（implicit differentiation）的方法求解梯度進行更新。

通過等價表示設計更多網絡

該方法不要求同一種算法只能對應一種結構，相反，該方法可以利用優化問題的等價表示設計更多的網絡架構，體現其靈活性。例如，線性化交替方向乘子法通常用于求解約束優化問題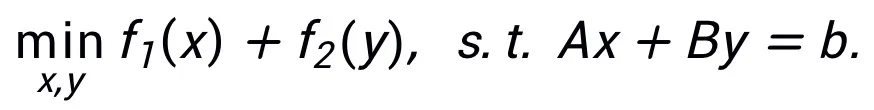：通過令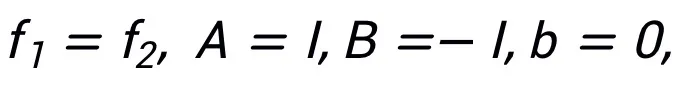即可得到一種可啟發網絡的更新迭代格式：

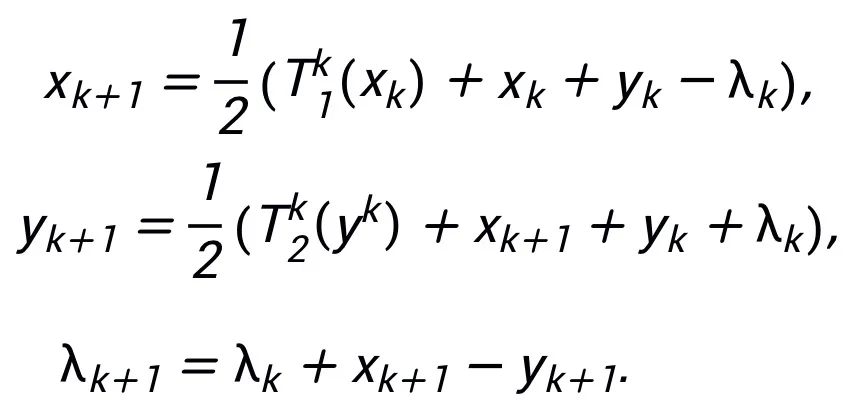
其啟發的網絡結構可見圖 2。

圖 2 線性化交替方向乘子法啟發的網絡結構

啟發的網絡具有萬有逼近性質

對該方法設計的網絡架構，可以證明，在模塊滿足此前條件以及優化算法（在一般情況下）穩定、收斂的條件下，任意一階優化算法啟發的神經網絡在高維連續函數空間具有萬有逼近性質，并給出了逼近速度。論文首次在有限寬度設定下證明了具有一般跨層連接的神經網絡的萬有逼近性質（此前研究基本集中在 FCNN 和 ResNet，見表 1），論文主定理可簡略敘述如下：

主定理（簡略版）：設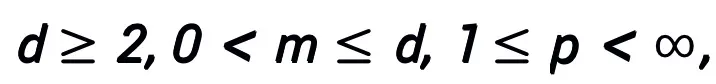 A 是一個梯度型一階優化算法。若算法 A 具有公式 (1) 中的更新格式，且滿足收斂性條件（優化算法的常用步長選取均滿足收斂性條件。若在啟發網絡中均為可學習的，則可以不需要該條件），則由算法啟發的神經網絡：

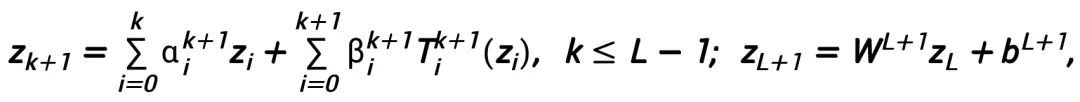
在連續（向量值）函數空間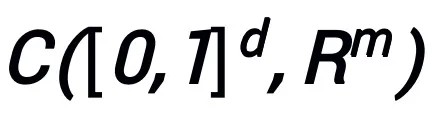以及范數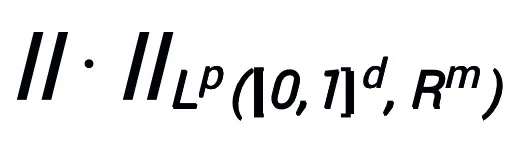下具有萬有逼近性質，其中可學習模塊 T 只要有包含兩層形如的結構（σ 可以是常用的激活函數）作為其子結構都可以。

常用的 T 的結構如：

1）卷積網絡中，pre-activation 塊：BN-ReLU-Conv-BN-ReLU-Conv (z),

2）Transformer 中：Attn (z) + MLP (z+Attn (z)).

主定理的證明利用了 NODE 的萬有逼近性質以及線性多步方法的收斂性質，核心是證明優化算法啟發設計的網絡結構恰對應一種收斂的線性多步方法對連續的 NODE 的離散化，從而啟發的網絡 “繼承” 了 NODE 的逼近能力。在證明中，論文還給出了 NODE 逼近 d 維空間連續函數的逼近速度，解決了此前論文 [6] 的一個遺留問題。

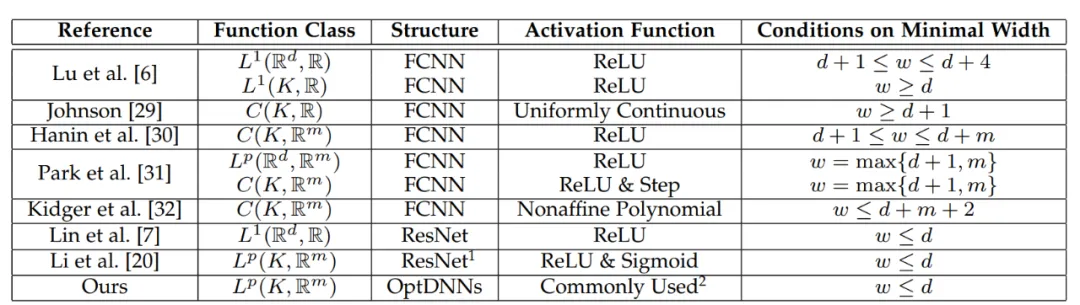
表 1 此前萬有逼近性質的研究基本集中在 FCNN 和 ResNet

實驗結果

論文利用所提出的網絡架構設計框架設計了 8 種顯式網絡和 3 種隱式網絡（稱為 OptDNN），網絡信息見表 2，并在嵌套環分離、函數逼近和圖像分類等問題上進行了實驗。論文還以 ResNet, DenseNet, ConvNext 以及 ViT 為 baseline，利用所提出的方法設計了改進的 OptDNN，并在圖像分類的問題上進行實驗，考慮準確率和 FLOPs 兩個指標。

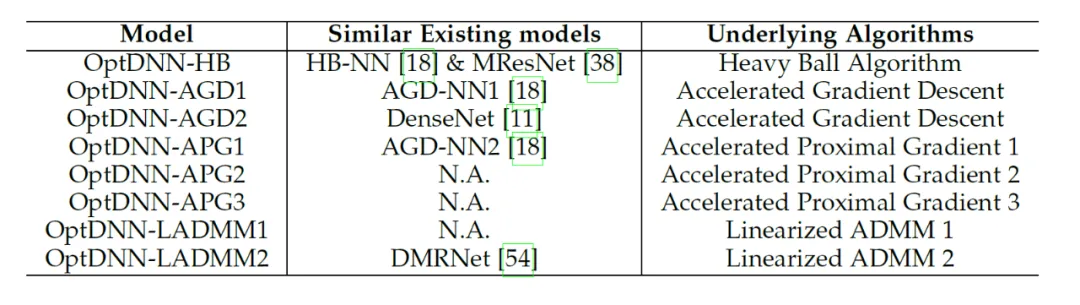
表 2 所設計網絡的有關信息

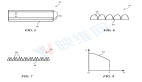
首先，OptDNN 在嵌套環分離和函數逼近兩個問題上進行實驗，以驗證其萬有逼近性質。在函數逼近問題中，分別考慮了逼近 parity function 和 Talgarsky function，前者可表示為二分類問題，后者則是回歸問題，這兩個問題都是淺層網絡難以逼近的問題。OptDNN 在嵌套環分離的實驗結果如圖 3 所示，在函數逼近的實驗結果如圖 3 所示，OptDNN 不僅取得了很好的分離 / 逼近結果，而且比作為 baseline 的 ResNet 取得了更大的分類間隔和更小的回歸誤差，足以驗證 OptDNN 的萬有逼近性質。

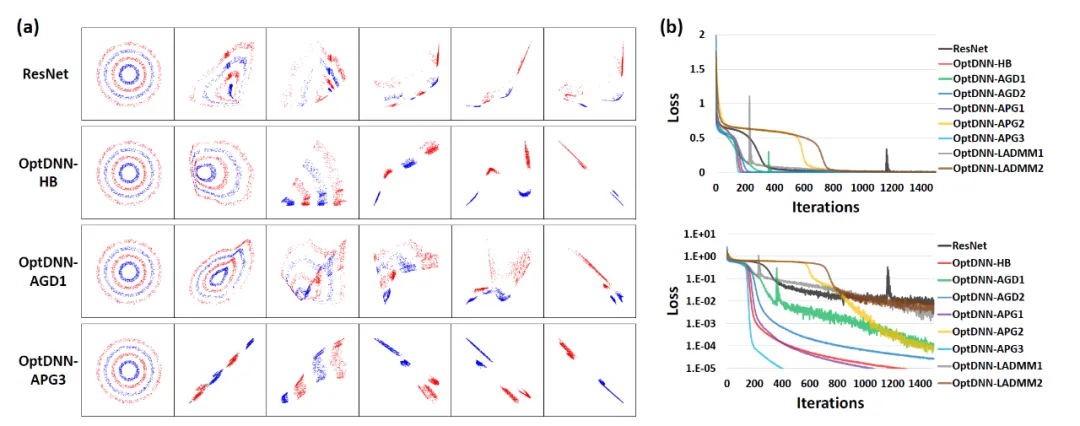
圖 3 OptNN 逼近 parity function

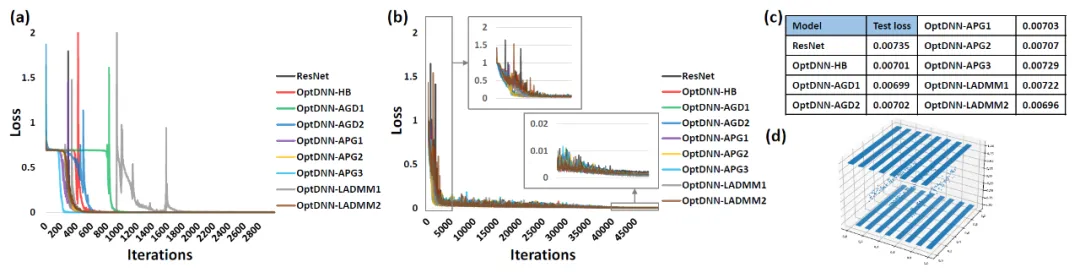
圖 4 OptNN 逼近 Talgarsky function

然后，OptDNN 分別在寬 - 淺和窄 - 深兩種設定下在 CIFAR 數據集上進行了圖像分類任務的實驗，結果見表 3 與 4。實驗均在較強的數據增強設定下進行，可以看出，一些 OptDNN 在相同甚至更小的 FLOPs 開銷下取得了比 ResNet 更小的錯誤率。論文還在 ResNet 和 DenseNet 設定下進行了實驗，也取得了類似的實驗結果。

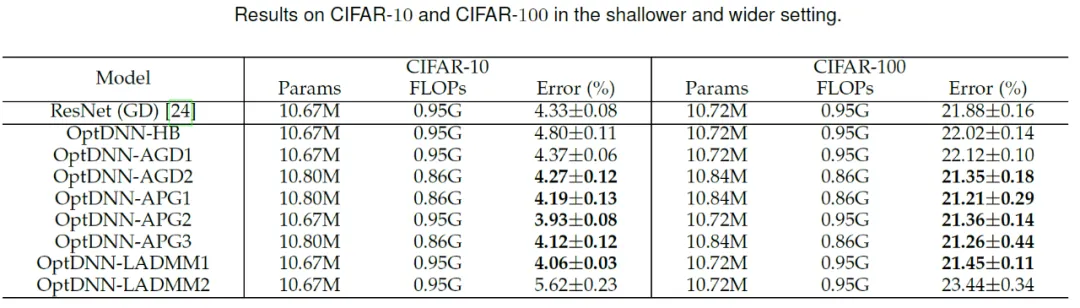
表 3 OptDNN 在寬 - 淺設定下的實驗結果

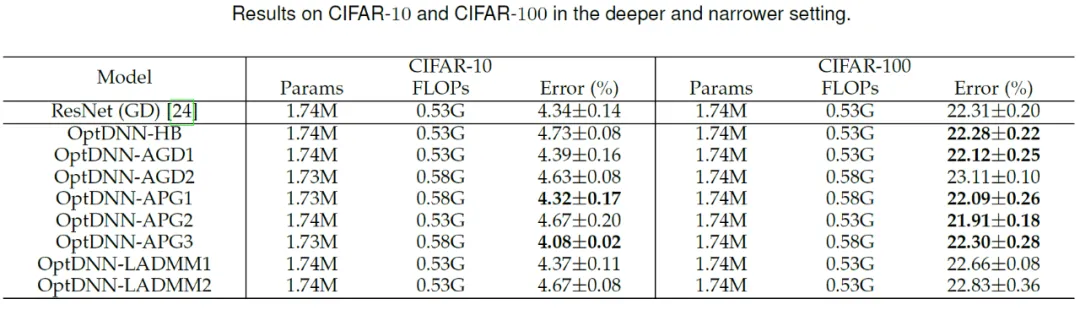
表 4 OptDNN 在窄 - 深設定下的實驗結果

論文進一步選取了此前表現較好的 OptDNN-APG2 網絡，進一步在 ConvNext 和 ViT 的設定下在 ImageNet 數據集上進行了實驗，OptDNN-APG2 的網絡結構見圖 5，實驗結果表 5、6。OptDNN-APG2 取得了超過等寬 ConvNext、ViT 的準確率，進一步驗證了該架構設計方法的可靠性。

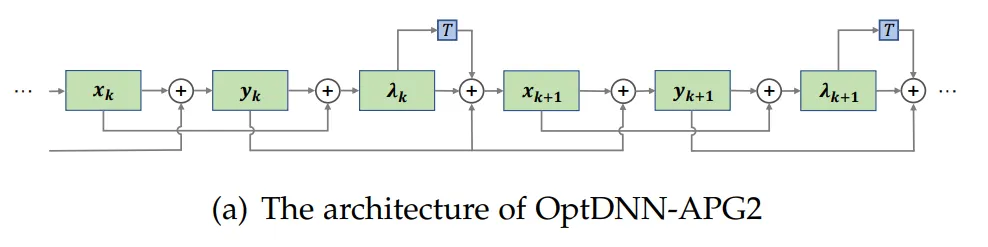
圖 5 OptDNN-APG2 的網絡結構

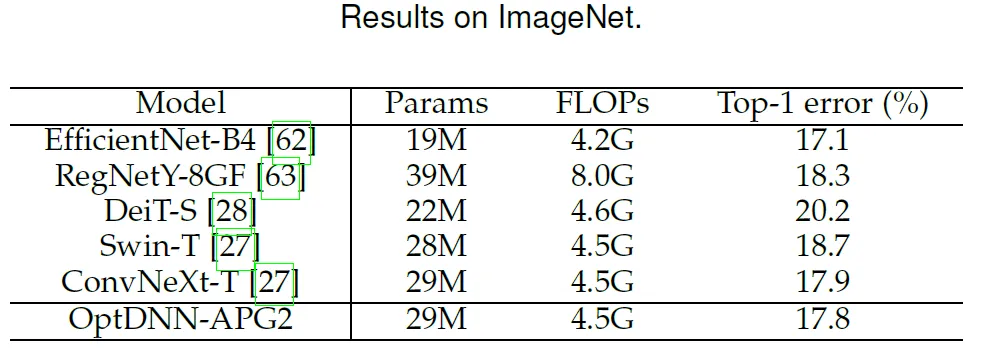
表 5 OptDNN-APG2 在 ImageNet 上的性能比較

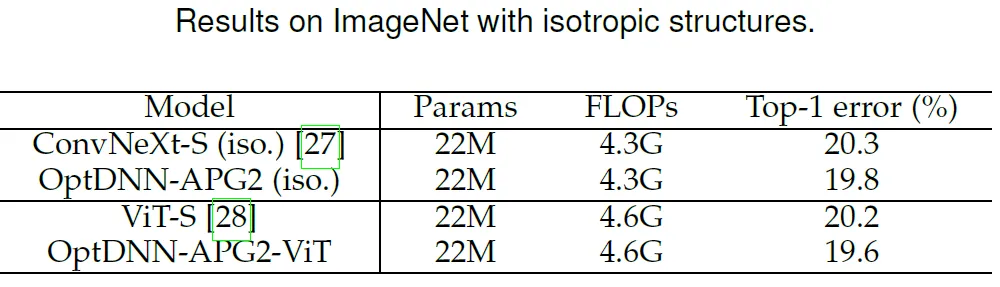
表 6 OptDNN-APG2 與等寬（isotropic）的 ConvNeXt 和 ViT 的性能比較

最后，論文依照 Proximal Gradient Descent 和 FISTA 等算法設計了 3 個隱式網絡，并在 CIFAR 數據集上和顯式的 ResNet 以及一些常用的隱式網絡進行了比較，實驗結果見表 7。三個隱式網絡均取得了與先進隱式網絡相當的實驗結果，也說明了方法的靈活性。

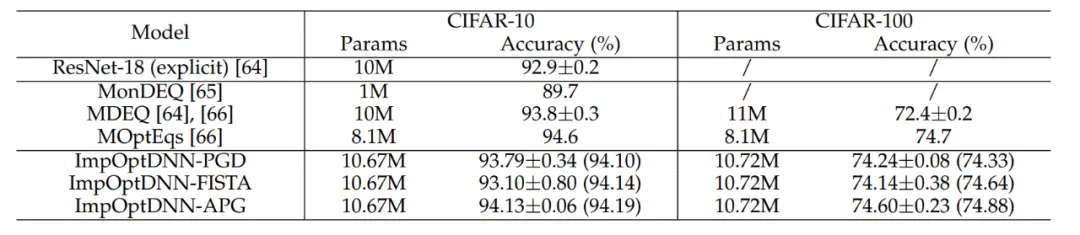
表 7 隱式網絡的性能比較

總結

神經網絡架構設計是深度學習中的核心問題之一。論文提出了一個利用一階優化算法設計具有萬有逼近性質保障的神經網絡架構的統一框架，拓展了基于優化設計網絡架構范式的方法。該方法可以與現有大部分聚焦網絡模塊的架構設計方法相結合，可以在幾乎不增加計算量的情況下設計出高效的模型。在理論方面，論文證明了收斂的優化算法誘導的網路架構在溫和條件下即具有萬有逼近性質，并彌合了 NODE 和具有一般跨層連接網絡的表示能力。該方法還有望與 NAS、 SNN 架構設計等領域結合，以設計更高效的網絡架構。