在本系列的 上一篇文章 中，我們回顧了人工智能的歷史，然后詳細地討論了矩陣。在本系列的第三篇文章中，我們將了解更多的矩陣操作，同時再介紹幾個人工智能 Python 庫。

在進入主題之前，我們先討論幾個人工智能和機器學習中常用的重要術語。人工神經網絡artificial neural network（通常簡稱為 神經網絡neural network，NN）是機器學習和深度學習的核心。顧名思義，它是受人腦的生物神經網絡啟發而設計的計算模型。本文中我沒有插入神經網絡模型的圖片，因為在互聯網上很容易找到它們。我相信任何對人工智能感興趣的人應該都見過它們，左邊是輸入層，中間是一個或多個隱藏層，右邊是輸出層。各層之間的邊上的 權重weight

監督學習supervised learning 和 無監督學習unsupervised learning

在實際的機器學習應用中會發生這樣的情況嗎？是的！訓練模型用的數據集可能是不充分的或者不完整的。這是兩種模型都仍然在人工智能和機器學習領域蓬勃發展的眾多原因之一。在后續文章中，我們將更正式地討論它們。下面我們開始學習使用 JupyterLab，它是一個用于開發人工智能程序的強大工具。

JupyterLab 入門

在本系列的前幾篇文章中，為了簡單起見，我們一直使用 Linux 終端運行 Python 代碼。現在要介紹另一個強大的人工智能工具——JupyterLab。在本系列的第一篇文章中，我們對比了幾個候選項，最終決定使用 JupyterLab。它比 Jupyter Notebook 功能更強大，為我們預裝了許多庫和包，并且易于團隊協作。還有一些其它原因，我們將在后續適時探討它們。

在本系列的第一篇文章中，我們已經學習了如何安裝 JupyterLab。假設你已經按文中的步驟安裝好了 JupyterLab，使用 jupyter lab 或 jupyter-lab 命令在會默認瀏覽器（如 Mozilla Firefox、谷歌 Chrome 等）中打開 JupyterLab。（LCTT 譯注：沒有安裝 JupyterLab 也不要緊，你可以先 在線試用 JupyterLab）圖 1 是在瀏覽器中打開的 JupyterLab 啟動器的局部截圖。JupyterLab 使用一個名為 IPython（交互式 Python）的 Python 控制臺。注意，IPython 其實可以獨立使用，在 Linux 終端運行 ipython 命令就可以啟動它。

圖 1：JupyterLab 啟動器

現階段我們使用 JupyterLab 中的 Jupyter Notebook 功能。點擊圖 1 中用綠框標記的按鈕，打開 Jupyter Notebook。這時可能會要求你選擇內核。如果你按照本系列第一篇的步驟安裝 JupyterLab，那么唯一的可選項就是 Python 3（ipykernel）。請注意，你還可以在 JupyterLab 中安裝其它編程語言的內核，比如 C++、R、MATLAB、Julia 等。事實上 Jupyter 的內核相當豐富，你可以訪問 Jupyter 內核清單 了解更多信息。

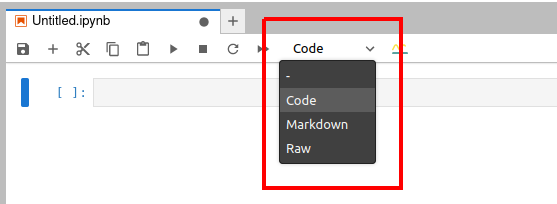圖 2：Jupyter Notebook 窗口

下面我們快速了解一下 Jupyter Notebook 的使用。圖 2 顯示的是一個在瀏覽器中打開的 Jupyter Notebook 窗口。從瀏覽器標簽頁的標題可以看出，Jupyter Notebook 打開的文件的擴展名是 .ipynb。

在圖 2 處可以看到有三個選項，它們表示 Jupyter Notebook 中可以使用的三種類型的單元。“Code”（綠色框） 表示代碼單元，它是用來執行代碼的。“Markdown” 單元可用于輸入說明性的文本。如果你是一名計算機培訓師，可以用代碼單元和 Markdown 單元來創建交互式代碼和解釋性文本，然后分享給你的學員。“Raw”（紅色框）表示原始數據單元，其中的內容不會被格式化或轉換。

和在終端中不同，在 Jupyter Notebook 中你可以編輯并重新運行代碼，這在處理簡單的拼寫錯誤時特別方便。圖 3 是在 Jupyter Notebook 中執行 Python 代碼的截圖。

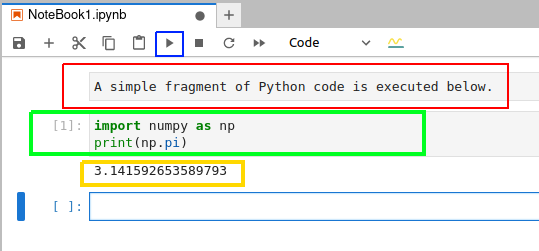圖 3：在 Jupyter Notebook 中執行 Python 代碼

要在執行代碼單元中的代碼，先選中該單元格，然后點擊藍框標記的按鈕。圖 3 中用紅框標記的是 Markdown 單元，用綠框標記的是代碼單元，用黃框標記的執行代碼的輸出。在這個例子中，Python 代碼輸出的是 π 的值。

前面提到，JupyterLab 默認安裝了許多庫和包，我們不用自己安裝了。你可以使用 import 命令將這些庫導入到代碼中。使用 !pip freeze 命令可以列出 JupyterLab 中目前可用的所有庫和包。如果有庫或包沒有安裝，大多數情況下都可以通過 pip install <全小寫的庫或者包的名稱> 來安裝它們。例如安裝 TensorFlow 的命令是 pip install tensorflow。如果后面有庫的安裝命令不遵循這個格式，我會進行特別說明。隨著本系列的繼續，我們還會看到 Jupyter Notebook 和 JupyterLab 更多強大的功能。

復雜的矩陣運算

通過下面的代碼，我們來了解一些更復雜的矩陣運算或操作。為了節省空間，我沒有展示代碼的輸出。

import numpy as np
A = np.arr ay([[1,2,3],[4,5,6],[7,8,88]])
B = np.arr ay([[1,2,3],[4,5,6],[4,5,6]])
print(A.T)
print(A.T.T)
print(np.trace(A))
print(np.linalg.det(A))
C = np.linalg.inv(A)
print(C)
print(A@C)

下面我逐行來解釋這些代碼：

1. 導入 NumPy 包。
2. 創建矩陣 A。
3. 創建矩陣 B。
4. 打印矩陣 A 的轉置transpose。通過比較矩陣 A 與 A 的轉置，你用該可以大致理解轉置操作到底做了什么。
5. 打印 A 的轉置的轉置。可以看到它和矩陣 A 是相同的。這又提示了轉置操作的含義。
6. 打印矩陣 A 的 跡trace。跡是矩陣的對角線（也稱為主對角線）元素的和。矩陣 A 的主對角線元素是 1、5 和 88，所以輸出的值是 94。
7. 打印 A 的行列式determinant。當執行代碼的結果是 -237.00000000000009（在你的電腦中可能略有區別）。因為行列式不為 0，所以稱 A 為非奇異矩陣non-singular matrix。
8. 將矩陣 A 的逆inverse 保存到矩陣 C 中。
9. 打印矩陣 C。
10. 打印矩陣 A 和 C 的乘積。仔細觀察，你會看到乘積是一個單位矩陣identity matrix，也就是一個所有對角線元素都為 1，所有其它元素都為 0 的矩陣。請注意，輸出中打印出的不是精確的 1 和 0。在我得到的答案中，有像 -3.81639165e-17 這樣的數字。這是浮點數的科學記數法，表示 -3.81639165 × 10^-17， 即小數的 -0.0000000000000000381639165，它非常接近于零。同樣輸出中的其它數字也會有這種情況。我強烈建議你了解計算機是怎樣表示浮點數的，這對你會有很大幫助。

根據第一篇文章中的慣例，可以將代碼分成基本 Python 代碼和人工智能代碼。在這個例子中，除了第 1 行和第 9 行之外的所有代碼行都可以被看作是人工智能代碼。

現在將第 4 行到第 10 行的操作應用到矩陣 B 上。從第 4 行到第 6 行代碼的輸出沒有什么特別之處。然而運行第 7 行時，矩陣 B 的行列式為 0，因此它被稱為奇異矩陣singular matrix。運行第 8 行代碼會給產生一個錯誤，因為只有非奇異矩陣才存在逆矩陣。你可以嘗試對本系列前一篇文章中的 8 個矩陣都應用相同的操作。通過觀察輸出，你會發現矩陣的行列式和求逆運算只適用于方陣。

方陣就是行數和列數相等的矩陣。在上面的例子中我只是展示了對矩陣執行各種操作，并沒有解釋它們背后的理論。如果你不知道或忘記了矩陣的轉置、逆、行列式等知識的話，你最好自己學習它們。同時你也應該了解一下不同類型的矩陣，比如單位矩陣、對角矩陣、三角矩陣、對稱矩陣、斜對稱矩陣。維基百科上的相關文章是不錯的入門。

現在讓我們來學習矩陣分解matrix decomposition，它是更復雜的矩陣操作。矩陣分解與整數的因子分解類似，就是把一個矩陣被寫成其它矩陣的乘積。下面我通過圖 4 中整數分解的例子來解釋矩陣分解的必要性。代碼單元開頭的 %time 是 Jupyter Notebook 的魔法命令magic command，它會打印代碼運行所花費的時間。** 是 Python 的冪運算符。基本的代數知識告訴我們，變量 a 和 b 的值都等于 (6869 x 7873)¹⁰⁰。但圖 4 顯示計算變量 b 的速度要快得多。事實上，隨著底數和指數的增大，執行時間的減少會越來越明顯。

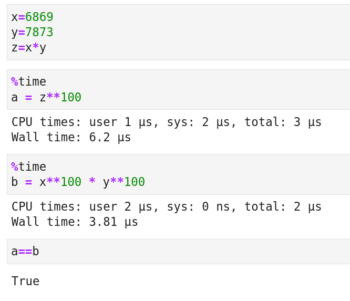圖 4：Python 代碼的執行耗時

在幾乎所有的矩陣分解技術技術中，原始矩陣都會被寫成更稀疏的矩陣的乘積。稀疏矩陣sparse matrix是指有很多元素值為零的矩陣。在分解后，我們可以處理稀疏矩陣，而不是原始的具有大量非零元素的密集矩陣dense matrix。在本文中將介紹三種矩陣分解技術——LUP 分解、特征分解eigen decomposition和奇異值分解singular value decomposition（SVD）。

為了執行矩陣分解，我們需要另一個強大的 Python 庫，SciPy。SciPy 是基于 NumPy 庫的科學計算庫，它提供了線性代數、積分、微分、優化等方面的函數。首先，讓我們討論 LUP 分解。任何方陣都能進行 LUP 分解。LUP 分解有一種變體，稱為 LU 分解。但并不是所有方陣都能 LU 分解。因此這里我們只討論 LUP 分解。

在 LUP 分解中，矩陣 A 被寫成三個矩陣 L、U 和 P 的乘積。其中 L 是一個下三角矩陣lower triangular matrix，它是主對角線以上的所有元素都為零的方陣。U 是一個上三角矩陣upper triangular matrix，它是主對角線以下所有元素為零的方陣。P 是一個排列矩陣permutation matrix。這是一個方陣，它的每一行和每一列中都有一個元素為 1，其它元素的值都是 0。

現在看下面的 LUP 分解的代碼。

import numpy as np
import scipy as sp
A=np.array([[11,22,33],[44,55,66],[77,88,888]])
P, L, U = sp.linalg.lu(A)
print(P)
print(L)
print(U)
print(P@L@U)

圖 5 顯示了代碼的輸出。第 1 行和第 2 行導入 NumPy 和 SciPy 包。在第 3 行創建矩陣 A。請記住，我們在本節中會一直使用矩陣 A。第 4 行將矩陣 A 分解為三個矩陣——P、L 和 U。第 5 行到第 7 行打印矩陣 P、L 和 U。從圖 5 中可以清楚地看出，P 是一個置換矩陣，L 是一個下三角矩陣，U 是一個上三角矩陣。最后在第 8 行將這三個矩陣相乘并打印乘積矩陣。從圖 5 可以看到乘積矩陣 P@L@U 等于原始矩陣 A，滿足矩陣分解的性質。此外，圖 5 也驗證了矩陣 L、U 和 P 比矩陣 A 更稀疏。

圖 5：用 SciPy 進行 LUP 分解

下面我們討論特征分解，它是將一個方陣是用它的特征值eigenvalue和特征向量eigenvector來表示。用 Python 計算特征值和特征向量很容易。關于特征值和特征向量的理論解釋超出了本文的討論范圍，如果你不知道它們是什么，我建議你通過維基百科等先了解它們，以便對正在執行的操作有一個清晰的概念。圖 6 中是特征分解的代碼。

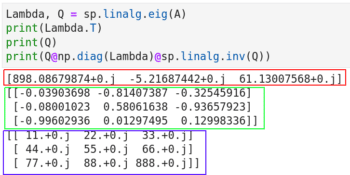圖6：用 SciPy 進行特征分解

在圖 6 中，第 1 行計算特征值和特征向量。第 2 行和第 3 行輸出它們。注意，使用 NumPy 也能獲得類似的效果，Lambda, Q = np.linalg.eig(A)。這也告訴我們 NumPy 和 SciPy 的功能之間有一些重疊。第 4 行重建了原始矩陣 A。第 4 行中的代碼片段 np.diag(Lambda) 是將特征值轉換為對角矩陣（記為 Λ）。對角矩陣是主對角線以外的所有元素都為 0 的矩陣。第 4 行的代碼片段 sp.linalg.inv(Q) 是求 Q 的逆矩陣（記為 Q^-1）。最后，將三個矩陣 Q、Λ、Q^-1 相乘得到原始矩陣 A。也就是在特征分解中 A=QΛQ^-1。

圖 6 還顯示了執行的代碼的輸出。紅框標記的是特征值，用綠框標記的是特征向量，重構的矩陣 A 用藍框標記。你可能會感到奇怪，輸出中像 11.+0.j 這樣的數字是什么呢？其中的 j 是虛數單位。11.+0.j 其實就是 11.0+0.0j，即整數 11 的復數形式。

現在讓我們來看奇異值分解（SVD），它是特征分解的推廣。圖 7 顯示了 SVD 的代碼和輸出。第 1 行將矩陣 A 分解為三個矩陣 U、S 和 V。第 2 行中的代碼片段 np.diag(S) 將 S 轉換為對角矩陣。最后，將這三個矩陣相乘重建原始矩陣 A。奇異值分解的優點是它可以對角化非方陣。但非方陣的奇異值分解的代碼稍微復雜一些，我們暫時不在這里討論它。

圖 7：用 SciPy 進行 奇異值分解

其它人工智能和機器學習的 Python 庫

當談到人工智能時，普通人最先想到的場景可能就是電影《終結者》里機器人通過視覺識別一個人。計算機視覺computer vision是人工智能和機器學習技術被應用得最廣泛的領域之一。下面我將介紹兩個計算機視覺相關的庫：OpenCV 和 Matplotlib。OpenCV 是一個主要用于實時計算機視覺的庫，它由 C 和 C++ 開發。C++ 是 OpenCV 的主要接口，它通過 OpenCV-Python 向用戶提供 Python 接口。Matplotlib 是基于 Python 的繪圖庫。我曾在 OSFY 上的一篇早期 文章 中詳細介紹了 Matplotlib 的使用。

前面我一直在強調矩陣的重要性，現在我用一個實際的例子來加以說明。圖 8 展示了在 Jupyter Notebook 中使用 Matplotlib 讀取和顯示圖像的代碼和輸出。如果你沒有安裝 Matplotlib，使用 pip install matplotlib 命令安裝 Matplotlib。

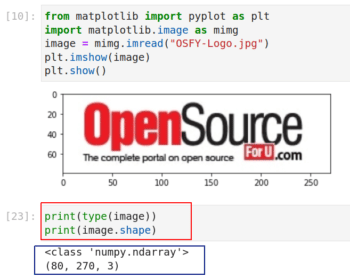圖 8：用 Matplotlib 讀取和顯示圖像

在圖 8 中，第 1 行和第 2 行從 Matplotlib 導入了一些函數。注意你可以從庫中導入單個函數或包，而不用導入整個庫。這兩行是基本的 Python 代碼。第 3 行從我的計算機中讀取標題為 OSFY-Logo.jpg 的圖像。我從 OSFY 門戶網站的首頁下載了這張圖片。此圖像高 80 像素，寬 270 像素。第 4 行和第 5 行在 Jupyter Notebook 窗口中顯示圖像。請注意圖像下方用紅框標記的兩行代碼，它的輸出告訴我們變量 image 實際上是一個 NumPy 數組。具體來說，它是一個 80 x 270 x 3 的三維數組。

數組尺寸中的 80 x 270 就是圖片的大小，這一點很容易理解。但是第三維度表示什么呢？這是因計算機像通常用 RGB 顏色模型來存儲的彩色圖。它有三層，分別用于表示紅綠藍三種原色。我相信你還記得學生時代的實驗，把原色混合成不同的顏色。例如，紅色和綠色混合在一起會得到黃色。在 RGB 模型中，每種顏色的亮度用 0 到 255 的數字表示。0 表示最暗，255 表示最亮。因此值為 (255,255,255) 的像素表示純白色。

現在，執行代碼 print(image)， Jupyter Notebook 會將整個數組的一部分部分打印出來。你可以看到數組的開頭有許多 255。這是什么原因呢？如果你仔細看 OSFY 的圖標會發現，圖標的邊緣有很多白色區域，因此一開始就印了很多 255。順便說一句，你還可以了解一下其他顏色模型，如 CMY、CMYK、HSV 等。

現在我們反過來從一個數組創建一幅圖像。首先看圖 9 中所示的代碼。它展示了如何生成兩個 3 x 3 的隨機矩陣，它的元素是 0 到 255 之間的隨機值。注意，雖然相同的代碼執行了兩次，但生成的結果是不同的。這是通過調用 NumPy 的偽隨機數生成器函數 randint 實現的。實際上，我中彩票的幾率都比這兩個矩陣完全相等的幾率大得多。

圖 8：兩個隨機矩陣

接下來我們要生成一個形狀為 512 x 512 x 3 的三維數組，然后將它轉換為圖像。為此我們將用到 OpenCV。注意，安裝 OpenCV 命令是 pip install opencv-python。看下面的代碼：

import cv2
img = np.random.randint(0, 256, size=(512, 512, 3))
cv2.imwrite('img.jpg', img)

第 1 行導入庫 OpenCV。注意導入語句是 import cv2，這與大多數其他包的導入不同。第 3 行將矩陣 img 轉換為名為 img.jpg 的圖像。圖 10 顯示了由 OpenCV 生成的圖像。在系統中運行這段代碼，將圖像將被保存在 Jupyter Notebook 的同一目錄下。如果你查看這張圖片的屬性，你會看到它的高度是 512 像素，寬度是 512 像素。通過這些例子，很容易看出，任何處理計算機視覺任務的人工智能和機器學習程序使用了大量的數組、向量、矩陣以及線性代數中的思想。這也是本系列用大量篇幅介紹數組、向量和矩陣的原因。

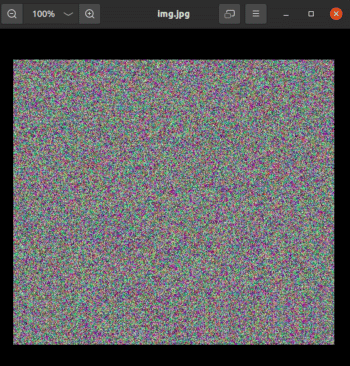圖 10：OpenCV 生成的圖像

最后，考慮下面顯示的代碼。image.jpg 輸出圖像會是什么樣子？我給你兩個提示。函數 zeros 在第 4 行和第 5 行創建了兩個 512 x 512 的數組，其中綠色和藍色填充了零。第 7 行到第 9 行用來自數組 red、green 和 blue 的值填充三維數組 img1。

import numpy as np
import cv2
red = np.random.randint(0, 256, size=(512, 512))
green = np.zeros([512, 512], dtype=np.uint8)
blue = np.zeros([512, 512], dtype=np.uint8)
img1 = np.zeros([512,512,3], dtype=np.uint8)
img1[:,:,0] = blue
img1[:,:,1] = green
img1[:,:,2] = red
cv2.imwrite(‘image.jpg’, img1)

本期的內容就到此結束了。在下一篇文章中，我們將開始簡單地學習張量tensor，然后安裝和使用 TensorFlow。TensorFlow 是人工智能和機器學習領域的重要參與者。之后，我們將暫時放下矩陣、向量和線性代數，開始學習概率論。概率論跟線性代數一樣是人工智能的重要基石。