11 月 13 日，微軟研究院（Microsoft Research）和普林斯頓大學研究人員，提出了一個通用框架，用于設計無監督學習問題的有效算法，如高斯分布和子空間聚類的混合。

研究人員所提的框架在解決噪聲問題上，使用了一種下界學習計算公式的元算法。這是建立在 Garg、Kayal 和 Saha (FOCS ’20) 最近的工作基礎上的，他們設計了這樣一個框架，用于在沒有任何噪音的情況下學習算術公式。元算法的一個關鍵要素是針對稱為“穩健向量空間分解”的新問題的有效算法。

研究證明，當某些矩陣具有足夠大的最小非零奇異值時，元算法效果很好。“我們推測這個條件適用于我們問題的平滑實例，因此我們的框架將為平滑設置中的這些問題產生有效的算法。”

該研究以《在存在噪聲的情況下學習算術公式：無監督學習的通用框架和應用》（Learning Arithmetic Formulas in the Presence of Noise: A General Framework and Applications to Unsupervised Learning）為題，于 11 月 13 日發布在 arXiv 預印平臺上。

無監督學習涉及發現數據中隱藏的模式和結構，而不使用任何標簽或直接的人類監督。

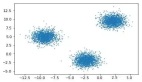
在這里，研究人員考慮具有良好數學結構或從數學上明確定義的分布生成的數據。前者的一個例子是，可以根據某些相似性模式將數據點分組為有意義的集群，并且目標是找到底層集群。后者的一個例子是混合建模，它假設數據是由簡潔描述的概率分布（例如高斯分布）的混合生成的，目標是從樣本中學習這些分布的參數。

解決許多無監督學習問題的通用框架是矩方法，它利用數據的統計矩來推斷模型的底層結構或底層參數。對于許多無監督學習問題場景，其中基礎數據具有一些很好的數學結構，數據的矩是參數的明確定義的函數。啟發式論證表明，相反的情況通常應該成立，即結構/分布的參數通常由數據的一些低階矩唯一確定。在這個大方向上，主要的挑戰是設計算法來（近似地）從（經驗）力矩中恢復潛在的參數。

我們還希望該算法高效、耐噪聲（即，即使僅近似而不是精確地知道矩，也能很好地工作），甚至是異常容忍度(即，即使少數數據點不符合底層結構/分布也能很好地工作)。但即使是該領域最簡單的問題也往往是 NP 困難的，并且即使沒有噪聲和異常值也仍然如此。

因此，人們實際上不能指望一種具有可證明的最壞情況保證的算法。但人們可以希望算法能夠保證通常運行良好，即對于隨機問題實例，或者更理想的是對于以平滑方式選擇的實例。因此，針對無監督學習中的每個此類問題設計了許多不同的算法，具有不同水平的效率、噪聲容忍度、離群值容忍度和可證明的保證。

在這項工作中，研究人員給出了一個適用于許多此類無監督學習問題的元算法。該研究的出發點是觀察到許多此類問題都歸結為學習算術公式的適當子類的任務。