圖神經網絡作為深度學習的一大活躍領域，受到人工智能學家廣泛關注。由于可以將圖論和深度學習緊密融合在一起，充分利用圖上拓撲信息，圖神經網絡為解決傳統深度學習單純歐氏空間中分析非歐氏空間的對稱性和傳遞性提供了思路。圖神經網絡的發展中，主要面臨兩大階段性挑戰。一方面，由于工業應用中圖多具有大規模特點，圖上傳統k-hop消息傳遞面臨指數增長的挑戰，對圖神經網絡獲取圖上深層拓撲信息產生障礙。另一方面，傳統圖神經網絡在圖同構測試和Weisfeiler-Lehman test仍有較大提升空間。

基于對子圖網絡應用的深入研究，Meta AI Research Scientist曾涵清博士對上述兩個問題分別提出新的思考；一方面，如何在不同任務中開發子圖的不同含義，從而降低大圖上的計算瓶頸并突破原始GNN的表達能力上限。當通過“等比例縮小”原圖得到子圖時，在子圖上訓練的GNN可以近似大規模全圖上訓練的GNN（基于模型的泛化能力）。由此引申出的一系列基于子圖采樣的工作大大降低了訓練的計算/存儲成本。另一方面，當把子圖視為原圖拓撲信息的增強時，我們可以從多種角度設計全新的GNN模塊（如子圖內以及跨子圖的消息傳遞）從而增強模型表達力。在經典的圖同構測試問題上，子圖GNN超越了理論上最強的全圖GNN。

展望未來，如何同時取得高效以及高表達能力仍是子圖GNN需要解決的重要問題。曾博士提供了一種思路，通過結合節點分類和圖分類兩個任務中的子圖GNN的核心模塊，以達到計算開銷和表達力的平衡。

一、圖神經網絡基礎知識

首先來介紹一下傳統圖神經網絡的概念、基本任務及面臨的挑戰，將子圖神經網絡應用于上述問題的基本思路，以及子圖神經網絡與全圖神經網絡的對比。

1、圖神經網絡與圖表示學習

圖表示學習任務可分為節點維度的信息嵌入、邊層面的信息嵌入及圖層面的信息嵌入。在節點層面，根據圖的輸入，產生針對每個點嵌入。在圖層面，對節點嵌入信息的池化可以得到圖層面的嵌入信息。

2、子圖圖神經網絡與圖神經網絡

①差異：子圖差異表現在拓撲信息的獲取、節點特征信息的提取、消息傳遞、池化層等方面。

②聯系：子圖作為全圖的一部分，對子圖進行計算產生的信息可以應用于全圖神經網絡的計算。

3、圖神經網絡現存問題

由于現實數據圖的固有特點，傳統圖神經網絡在工業應用中往往面臨多種問題，具體表現為可擴展性問題和表達力問題。一方面，工業應用中圖的節點數往往遠大于實驗用圖數據，由此產生的計算復雜度往往使得全圖神經網絡難以真正被用于圖數據的計算。設計出可以用于大規模圖數據的圖神經網絡，是圖神經網絡亟待解決的問題。另一方面，為了區分圖數據中不同節點的信息，圖神經網絡應可以對不同相似節點產生不同節點嵌入信息。在對節點的分析中，傳統以消息傳遞為基礎的圖神經網絡的理論上限被證明為1-WL，如何設計出高區分度的圖神經網絡，也是圖神經網絡面臨的挑戰。

4、最近的工作

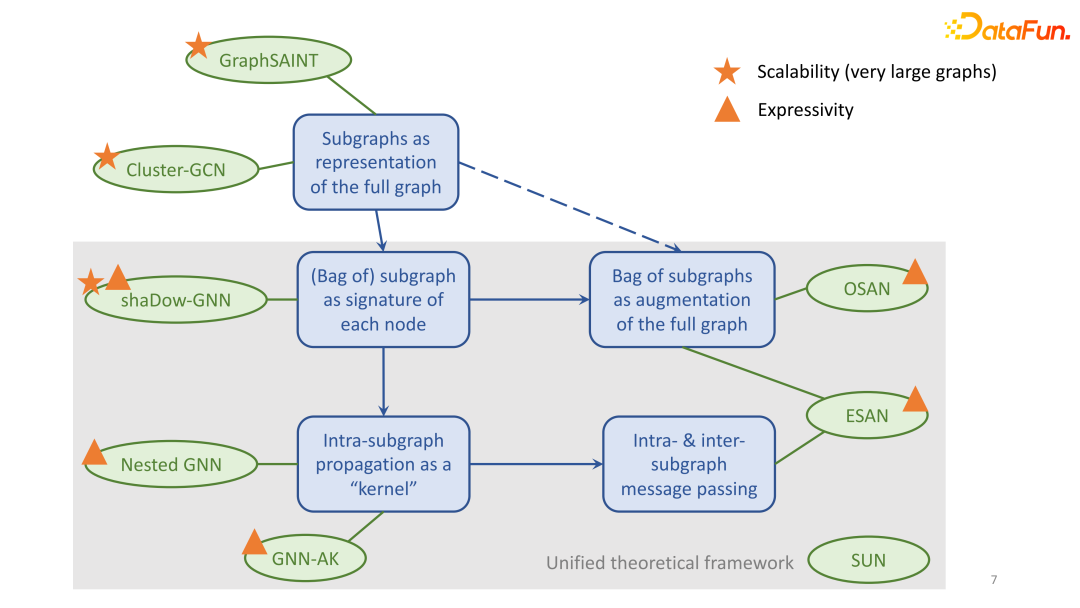
下圖中列出了最近的一些工作，并標出了每篇文章關注的重點。

二、子圖神經網絡與可擴展性

針對上述圖神經網絡的挑戰，曾博士從子圖神經網絡角度提出了思考。通過對經典子圖神經網絡算法GraphSIANT的分析，剖析子圖神經網絡的可擴展性方法。

1、圖訓練：小批量訓練

對數據容量小于原圖但保留原圖特征的子圖進行圖神經網絡計算，可以使得圖神經網絡訓練在近似原圖訓練的同時減少計算復雜度。另外，由于子圖中消息傳遞的節點數小于總節點數，通過設定子圖節點數，子圖神經網絡鄰居點數可以被限制在一定有效范圍內，從防止鄰居節點指數級增長帶來計算復雜度。

2、GraphSAINT基于子圖采樣的普適圖訓練架構

小批量訓練在訓練中體現出的性能建立在采樣方法可以以小樣本采集到原圖結構信息基礎上。如何能夠設計出可表征原圖信息的子圖采樣方法，成為小批量訓練的關鍵問題。

曾博士提出的GraphSAINT框架，第一步，基于importance node/edge sampling、Random-walk及其變種等采樣算法，采樣子圖。第二步，利用神經網絡對子圖進行計算。GraphSAINT還加入了normalization以減小不同采樣算法之間差異帶來的影響，同時利用variance reduction增強對重要子圖的提取能力，以增強子圖采樣的整體可信度并利用隨機性采樣增加泛化能力。另外，Cluster-GNN也可視為子圖神經網絡采樣的一種方案。

綜上，子圖神經網絡的第一種應用方法可概括為設計采樣方式在原圖中采樣能夠反映原圖信息的子圖，以此降低計算復雜度并對產生與全圖神經網絡相近的計算結果。

三、子圖神經網絡與表達力

傳統圖神經網絡被證明以1-WL為表達力上限，如何設計出能夠依據圖產生更多信息，并以此增加圖神經網絡的表達能力，也是圖神經網絡亟待解決的問題。

1、圖表達力的子圖應用

圖神經網絡表達能力的評判，關鍵在于算法能否區分相似但不同的“regular graph”。在曾博士看來，當引入子圖時，一個重要的直覺就是“regular graph的子圖不一定是regular的” –- 全局（全圖）的對成型被局部（子圖）的不對稱所打破。所以在這樣的子圖上運行1WL（及相對應的GNN），我們就可以區分出這兩個圖不同構。

2、Shadow-GNN：子圖與節點分類

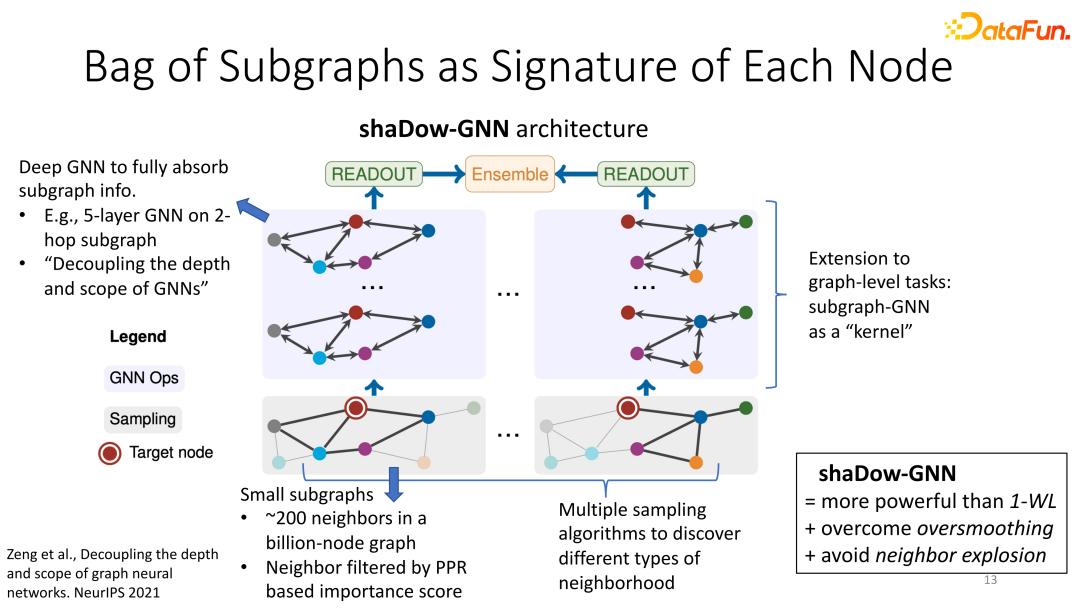
不同于GraphSAINT，在shaDow-GNN看來，每個子圖不再代表全圖的性質，而是作為每個目標節點的一個“指紋”。整體architecture如下：對每個目標節點，我們在其周圍提取一個小的臨域子圖（這里“小”可以是幾億節點的全圖中的200個節點構成的子圖，這200個節點可以通過Personalized PageRank score或其他方法進行filter）；這個小的子圖可能只包含目標節點的一（小）部分1-hop與2-hop neighbor，但是我們在這個淺層的子圖里運用一個深層的GNN（比如5層），以保證子圖的信息能夠被模型徹底吸收提取。注意這里GNN的層數（比如5）不再直接與子圖的深度（比如2）掛鉤，所以我們說這個模型是decoupled。進一步拓展，每個目標節點可以由多個臨域子圖來描述，這樣我們就有多個GNN并行地提取subgraph embedding，最后通過ensemble得到目標節點的embedding。

3、子圖神經網絡與圖分類

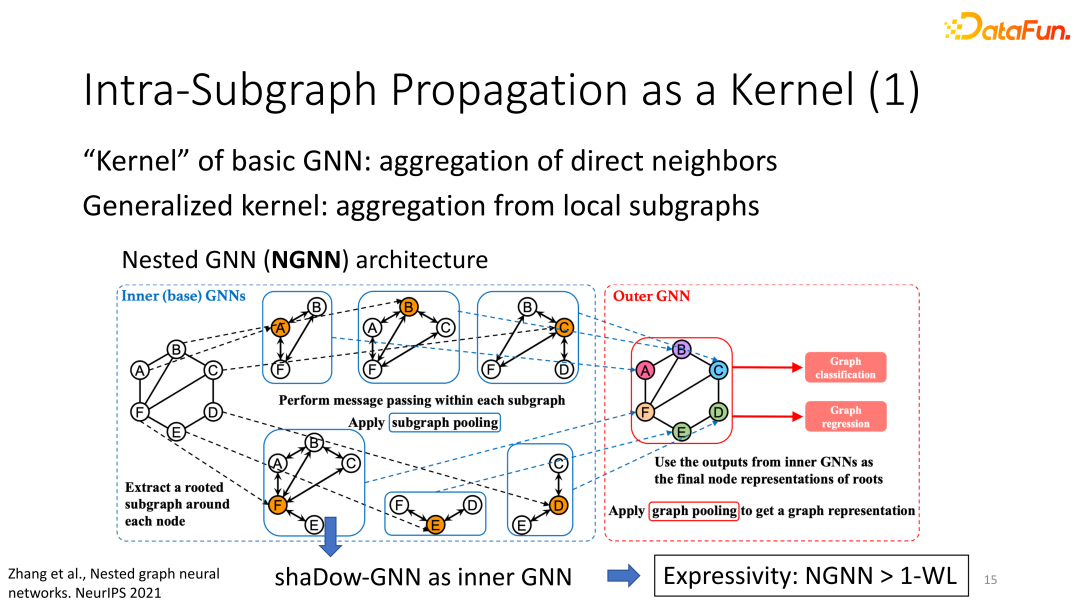
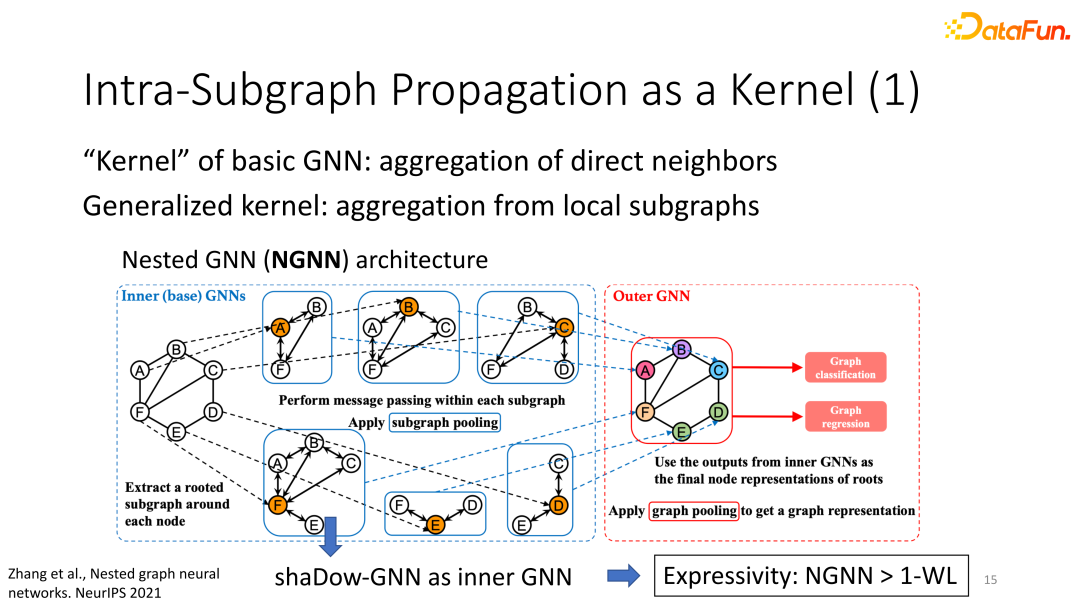
（1）思路：傳統GNN的kernel是對所有直接鄰居的信息聚合，而subgraph-GNN的kernel是對整個subgraph的多層的信息聚合。

（2）Nested GNN：內層（inner）GNN類似于shaDow-GNN的操作：對每個節點取一個鄰居子圖，然后對此子圖跑多層的GNN生成subgraph embedding。外層（outer）GNN對所有內層GNN的subgraph embedding再做了一次全局的pooling，從而得到整個全圖的embedding，以此對全圖生成預測的標簽。由于shaDow-GNN超越了1WL的表達力，Nested GNN也超越了1WL。

（3）GNN-AK：GNN-AK進一步拓展了kernel的用法，它是Nested GNN的一種衍生模型。Nested GNN在全圖層面對所有subgraph embedding做了一次信息聚合，而GNN-AK則進行了多次subgraph embedding的聚合。直觀來看，GNN-AK是把多個Nested GNN疊加，相當于一個多層的Nested GNN。這樣的模型層面的拓展也帶來表達能力的提升。理論上GNN-AK也超越了1WL；GNN-AK可以區分某一些3WL不能區分的圖。如果我們對每個節點取一種特殊的鄰居subgraph，即k-hop subgraph，那么當k增大時，GNN-AK的表達能力也得到提升。這說明更大的subgraph包含更多信息，進而更能提升表達力。

（4）OSAN and ESAN:信息增強：OSAN的子圖集合定義為所有k個節點可能組成的子圖。該子圖用來生成1-WL的初始顏色（由于GNN和1WL的等價性，拓展1WL的初始顏色相當于增強每個GNN節點的初始特征）。每個節點和每個k指定大小子圖匹配起來都可以生成一組初始顏色。這樣相比于原始的1-WL（每個節點只有一種初始顏色），OSAN的消息傳遞的信息更加豐富。并且由于k-sized subgraph包含了原圖的結構信息，由子圖生成的新的信息也使得GNN可以提取更豐富的結構信息。公式展示了每次WL迭代中更新顏色的過程。一式對應原始的WL，二式對應基于子圖的WL。下面的C（v，g）表示此處v的顏色也取決于子圖g。

表達能力方面，OSAN在增大k值時表達能力逐漸增強。

另一經典應用為ESAN：利用子圖，增加信息傳遞的種類。

與在構建的子圖上進行獨立的信息傳遞不同的是，ESAN增加了新的信息傳遞操作：子圖間的信息傳遞。即在不同圖同時進行神經網絡計算，并對不同子圖的同一層輸出進行信息整合，形成“子圖間”的信息傳遞，達到豐富信息傳遞的目的。

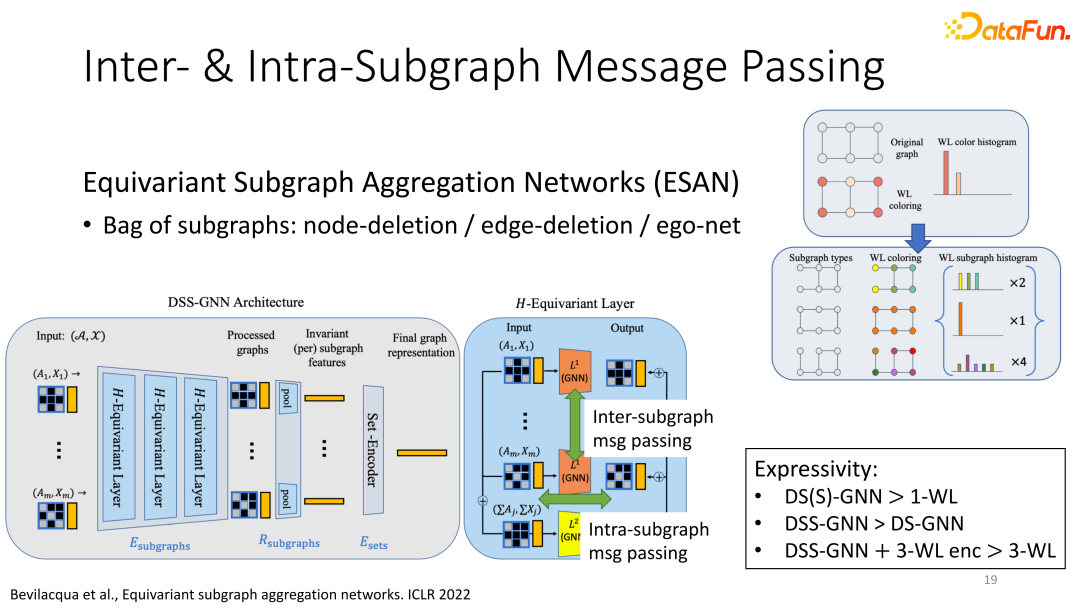
（右圖：基于edge-deletion的子圖構建方法：在原圖中的所有邊中刪除一條邊后得到的子圖就是ESAN的一個子圖。并展示了對原圖的多種刪除邊方法。）

四、未來展望

1、問題與解決

同一計算方法，對于可擴展性和表達力的提升往往處于矛盾狀態：表達能力強的subgraph-GNN計算起來不高效。主要原因為：① GNN需要處理非常多的子圖，每個子圖大小差異巨大。②K步子圖包含的子圖數目及節點數隨著k的增加呈指數級增加。③node-deleted subgraph個數等于全圖的節點個數。曾博士給出的解決方式為進一步采樣，即在子圖集合中采樣部分數據用于訓練。但是如何在進一步采樣時減少表達能力的損失，仍需要更多的研究。

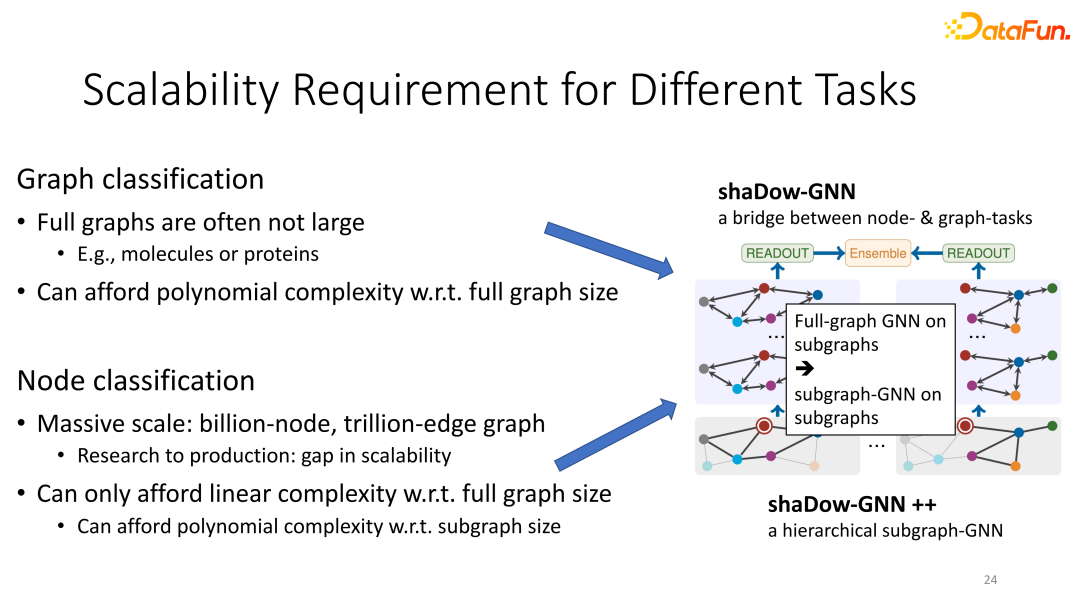
針對不同下游任務，圖神經網絡面臨的挑戰也有所不同：圖嵌入任務多用于分子圖等小型圖數據，而節點分類更多用于社交網絡等大規模圖計算，因此需要更多精力解決圖神經網絡的可擴展性問題。

2、未來展望

展望未來，我們可以以shaDow-GNN為基本框架，結合為節點分類和圖分類兩種任務設計的不同的subgraphGNN，從而取得節點分類任務中對超巨圖的expressivity與scalability的更好的平衡。我們可以在巨大的社交網絡里抽取小的子圖，然后在小的子圖上運行那些為圖分類問題設計，表達能力更高但計算成本也更高的subgraph-GNN。這樣我們既提升了shaDow-GNN的表達能力，又仍然服從模型整體復雜度的要求（相對全圖的線性復雜度；相對小的子圖的多項式復雜度）