使用Pandas和Python從時間序列數(shù)據(jù)中提取有意義的特征，包括移動平均，自相關和傅里葉變換。

前言

時間序列分析是理解和預測各個行業(yè)(如金融、經(jīng)濟、醫(yī)療保健等)趨勢的強大工具。特征提取是這一過程中的關鍵步驟，它涉及將原始數(shù)據(jù)轉換為有意義的特征，可用于訓練模型進行預測和分析。在本文中，我們將探索使用Python和Pandas的時間序列特征提取技術。

在深入研究特征提取之前，讓我們簡要回顧一下時間序列數(shù)據(jù)。時間序列數(shù)據(jù)是按時間順序索引的數(shù)據(jù)點序列。時間序列數(shù)據(jù)的例子包括股票價格、溫度測量和交通數(shù)據(jù)。時間序列數(shù)據(jù)可以是單變量，也可以是多變量。單變量時間序列數(shù)據(jù)只有一個變量，而多變量時間序列數(shù)據(jù)有多個變量。

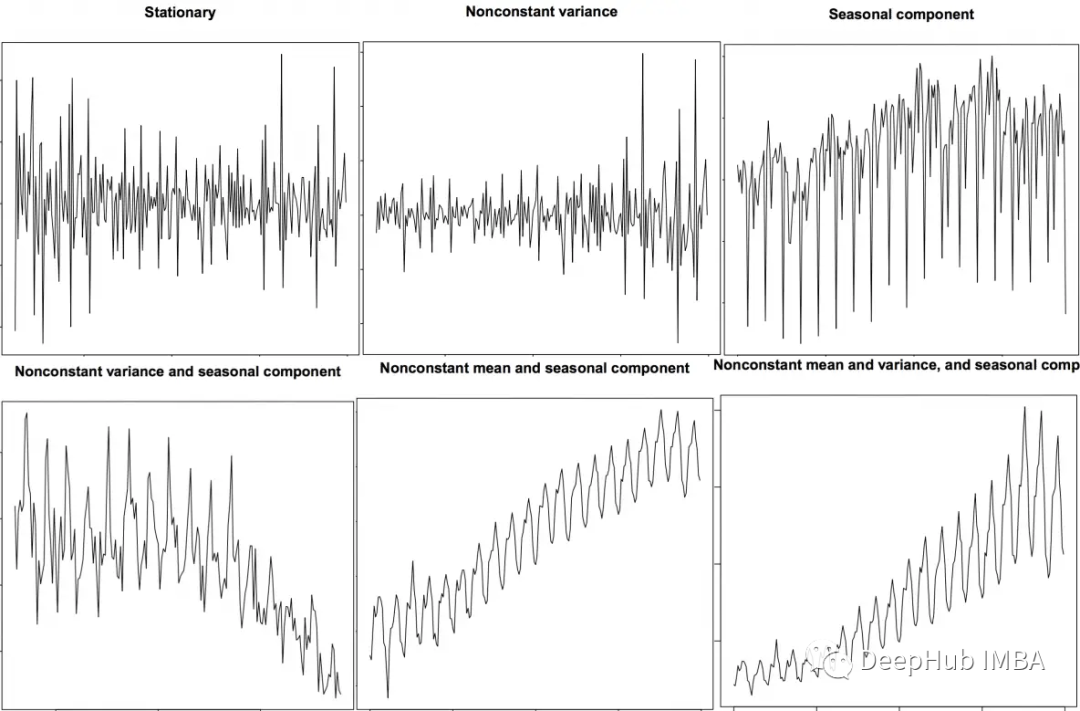
有各種各樣的特征提取技術可以用于時間序列分析。在本文中，我們將介紹以下技術:

• Resampling
• Moving Average
• Exponential Smoothing
• Autocorrelation
• Fourier Transform

1、Resampling

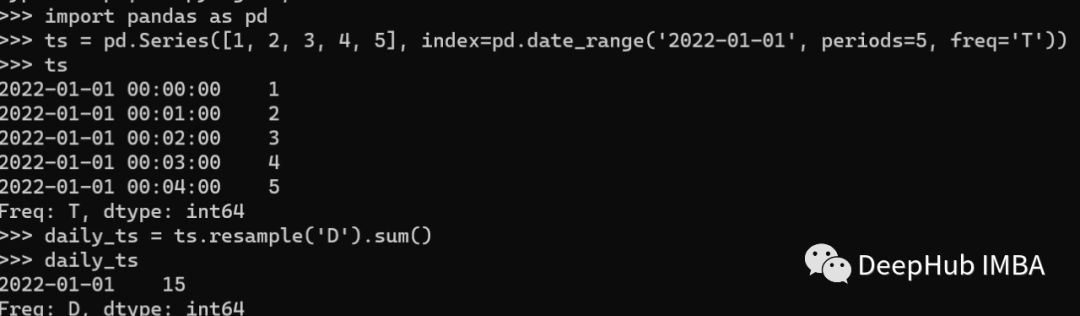
Resampling 重采樣主要是改變時間序列數(shù)據(jù)的頻率。這對于平滑噪聲或?qū)?shù)據(jù)采樣到較低的頻率很有用。Pandas提供了resample()方法對時間序列數(shù)據(jù)進行重新采樣。resample()方法可用于對數(shù)據(jù)進行上采樣或下采樣。下面是一個如何將時間序列降采樣到每日頻率的示例:

import pandas as pd
 
 # create a time series with minute frequency
 ts = pd.Series([1, 2, 3, 4, 5], index=pd.date_range('2022-01-01', periods=5, freq='T'))
 
 # downsample to daily frequency
 daily_ts = ts.resample('D').sum()
 
 print(daily_ts)

在上面的例子中，我們創(chuàng)建了一個以分鐘為頻率的時間序列，然后使用resample()方法將其采樣到每天的頻率。

2、Moving Average

Moving Average 移動平均是一種通過在滾動窗口上求平均值來平滑時間序列數(shù)據(jù)的技術。可以幫助去除噪聲并得到數(shù)據(jù)的趨勢。Pandas提供了rolling()方法來計算時間序列的平均值。下面是一個如何計算時間序列的平均值的例子:

import pandas as pd
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the rolling mean with a window size of 3
 rolling_mean = ts.rolling(window=3).mean()
 
 print(rolling_mean)

我們創(chuàng)建了一個時間序列，然后使用rolling()方法計算窗口大小為3的移動平均值。

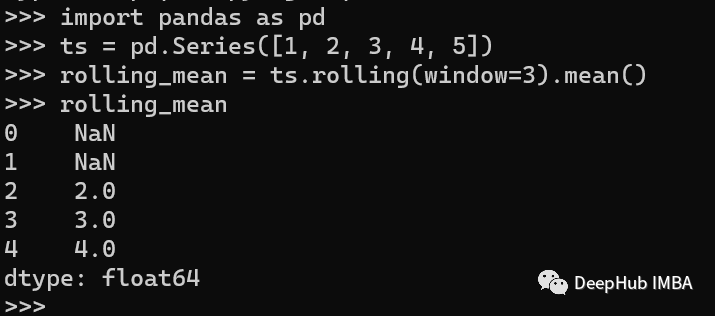
可以看到前兩個值因為沒有到達移動平均的最小數(shù)量3，所以會產(chǎn)生NAN，如果需要的話可以再使用fillna方法進行填充。

3、Exponential Smoothing

Exponential Smoothing 指數(shù)平滑是一種通過賦予最近值更多權重來平滑時間序列數(shù)據(jù)的技術。它可以幫助去除噪聲獲得數(shù)據(jù)的趨勢。Pandas提供了計算指數(shù)移動平均的ewm()方法。

import pandas as pd
 ts = pd.Series([1, 2, 3, 4, 5])
 ts.ewm( alpha =0.5).mean()

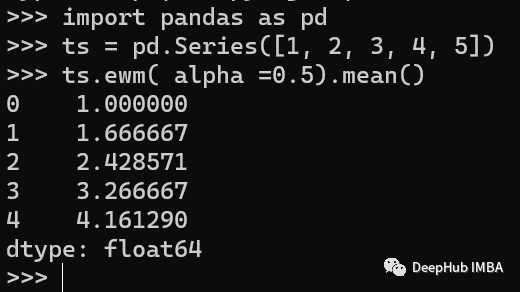
在上面的例子中，我們創(chuàng)建了一個時間序列，然后使用ewm()方法計算平滑因子為0.5的指數(shù)移動平均。

ewm有很多的參數(shù)，這里我們介紹幾個主要的。

com：根據(jù)質(zhì)心指定衰減

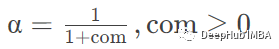
span 根據(jù)范圍指定衰減

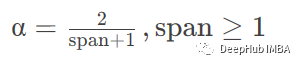
halflife 根據(jù)半衰期指定衰減

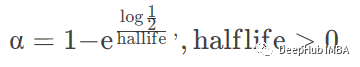
alpha 指定平滑系數(shù)α

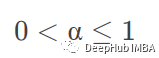
以上4個參數(shù)都是指定平滑系數(shù)α，只是前三個是根據(jù)條件計算出來的，最后一個是手動指定，所以至少要有一個，例如上面的例子我們就直接手動設定了0.5

min_periods 窗口中具有值的最小觀察數(shù)，默認 0。

adjust 是否進行誤差修正 默認True。

adjust =Ture時公式如下：

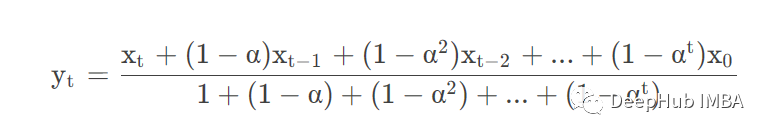
adjust =False

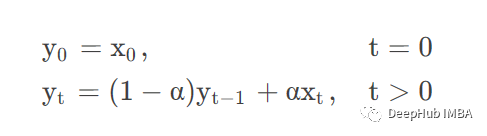
4、Autocorrelation

Autocorrelation 自相關是一種用于測量時間序列與其滯后版本之間相關性的技術。可以識別數(shù)據(jù)中重復的模式。Pandas提供了autocorr()方法來計算自相關性。

import pandas as pd
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the autocorrelation with a lag of 1
 autocorr = ts.autocorr(lag=1)
 
 print(autocorr)

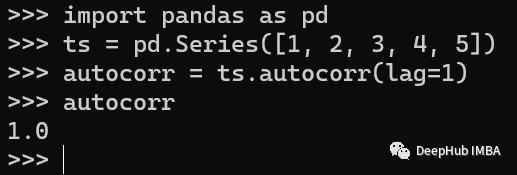
5、Fourier Transform

Fourier Transform 傅里葉變換是一種將時間序列數(shù)據(jù)從時域變換到頻域的技術。可以識別數(shù)據(jù)中的周期性模式。我們可以使用numpy的fft()方法來計算時間序列的快速傅里葉變換。

import pandas as pd
 import numpy as np
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the Fourier transform
 fft = pd.Series(np.fft.fft(ts).real)
 
 print(fft)

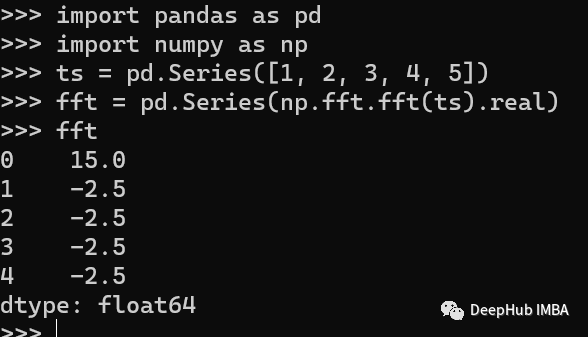
這里我們只顯示了實數(shù)的部分。

總結

在本文中，我們介紹了幾種使用Python和Pandas的時間序列特征提取技術。這些技術可以幫助將原始時間序列數(shù)據(jù)轉換為可用于分析和預測的有意義的特征，在訓練機器學習模型時，這些特征都可以當作額外的數(shù)據(jù)輸入到模型中，可以增加模型的預測能力。