AI驅動運籌優化「光刻機」!中科大等提出分層序列模型,大幅提升數學規劃求解效率
數學規劃求解器因其重要性和通用性,被譽為運籌優化領域的「光刻機」。
其中,混合整數線性規劃 (Mixed-Integer Linear Programming, MILP) 是數學規劃求解器的關鍵組件,可建模大量實際應用,如工業排產,物流調度,芯片設計,路徑規劃,金融投資等重大領域。
近期,中科大 MIRA Lab 王杰教授團隊和華為諾亞方舟實驗室聯合提出分層序列模型(Hierarchical Sequence Model, HEM),大幅提升混合整數線性規劃求解器求解效率,相關成果發表于ICLR 2023。
目前,算法已整合入華為 MindSpore ModelZoo 模型庫,相關技術和能力并將于今年內整合入華為天籌(OptVerse)AI求解器。該求解器旨在將運籌學和AI相結合,突破業界運籌優化極限,助力企業量化決策和精細化運營,實現降本增效!

作者列表:王治海*,李希君*,王杰**,匡宇飛,袁明軒,曾嘉,張勇東,吳楓
論文鏈接:https://openreview.net/forum?id=Zob4P9bRNcK
開源數據集:https://drive.google.com/drive/folders/1LXLZ8vq3L7v00XH-Tx3U6hiTJ79sCzxY?usp=sharing
PyTorch 版本開源代碼:https://github.com/MIRALab-USTC/L2O-HEM-Torch
MindSpore 版本開源代碼:https://gitee.com/mindspore/models/tree/master/research/l2o/hem-learning-to-cut
天籌(OptVerse)AI求解器:https://www.huaweicloud.com/product/modelarts/optverse.html
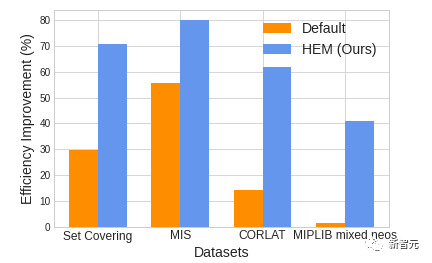
圖1. HEM 與求解器默認策略(Default)求解效率對比,HEM 求解效率最高可提升 47.28%
1 引言
割平面(cutting planes, cuts)對于高效求解混合整數線性規劃問題至關重要。
其中割平面選擇(cut selection)旨在選擇待選割平面的恰當子集以提高求解 MILP 的效率。割平面選擇在很大程度上取決于兩個子問題: (P1)應優先選哪些割平面,以及(P2)應選擇多少割平面。
盡管許多現代 MILP 求解器通過手動設計的啟發式方法來處理 (P1) 和 (P2),但機器學習方法有潛力學習更有效的啟發式方法。
然而,許多現有的學習類方法側重于學習應該優先選擇哪些割平面,而忽略了學習應該選擇多少割平面。此外,我們從大量的實驗結果中觀察到又一子問題,即(P3)應該優先選擇哪種割平面順序,對求解 MILP 的效率也有重大影響。
為了應對這些挑戰,我們提出了一種新穎的分層序列模型(Hierarchical Sequence Model, HEM),并通過強化學習框架來學習割平面選擇策略。
據我們所知,HEM 是首個可同時處理(P1),(P2)和(P3)的學習類方法。實驗表明,在人工生成和大規模真實世界 MILP 數據集上,與人工設計和學習類基線相比,HEM 大幅度提高了求解 MILP 的效率。
2 背景與問題介紹
2.1 割平面(cutting planes, cuts)介紹
混合整數線性規劃(Mixed-Integer Linear Programming, MILP)是一種可廣泛應用于多種實際應用領域的通用優化模型,例如供應鏈管理 [1]、排產規劃 [2]、規劃調度 [3]、工廠選址 [4]、裝箱問題 [5]等。
標準的MILP具有以下形式:
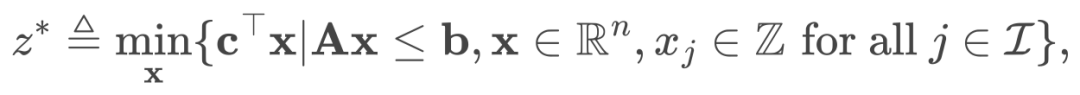
(1)
給定問題(1),我們丟棄其所有整數約束,可得到線性規劃松弛(linear programming relaxation, LPR)問題,它的形式為:
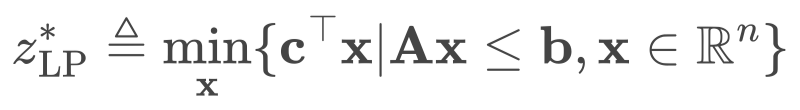
(2)
由于問題(2)擴展了問題(1)的可行集,因此我們可有,即 LPR 問題的最優值是原 MILP 問題的下界。
給定(2)中的 LPR 問題,割平面(cutting planes, cuts)是一類合法線性不等式,這些不等式在添加到線性規劃松弛問題中后,可收縮 LPR 問題中的可行域空間,且不去除任何原 MILP 問題中的整數可行解。
2.2 割平面選擇(cut selection)介紹
MILP 求解器在求解 MILP 問題過程中可生成大量的割平面,且會在連續的回合中不斷向原問題中添加割平面。
具體而言,每一回合中包括五個步驟:
(1)求解當前的 LPR 問題;
(2)生成一系列待選割平面;
(3)從待選割平面中選擇一個合適的子集;
(4)將選擇的子集添加到 (1) 中的 LPR 問題,以得到一個新的 LPR 問題;
(5)循環重復,基于新的 LPR 問題,進入下一個回合。
將所有生成的割平面添加到 LPR 問題中可最大程度地收縮該問題的可行域空間,以最大程度提高下界。
然而,添加過多的割平面可能會導致問題約束過多,增加問題求解計算開銷并出現數值不穩定問題 [6,7]。
因此,研究者們提出了割平面選擇(cut selection),割平面選擇旨在選擇候選割平面的適當子集,以盡可能提升 MILP 問題求解效率。割平面選擇對于提高解決混合整數線性規劃問題的效率至關重要 [8,9,10]。
2.3 啟發實驗——割平面添加順序
我們設計了兩種割平面選擇啟發式算法,分別為 RandomAll 和 RandomNV(詳見原論文第3章節)。
它們都在選擇了一批割平面后,以隨機順序將選擇的割平面添加到 MILP 問題中。如圖2結果顯示,選定同一批割平面的情況下,以不同的順序添加這些選定割平面對求解器求解效率有極大的影響(詳細結果分析見原論文第3章節)。
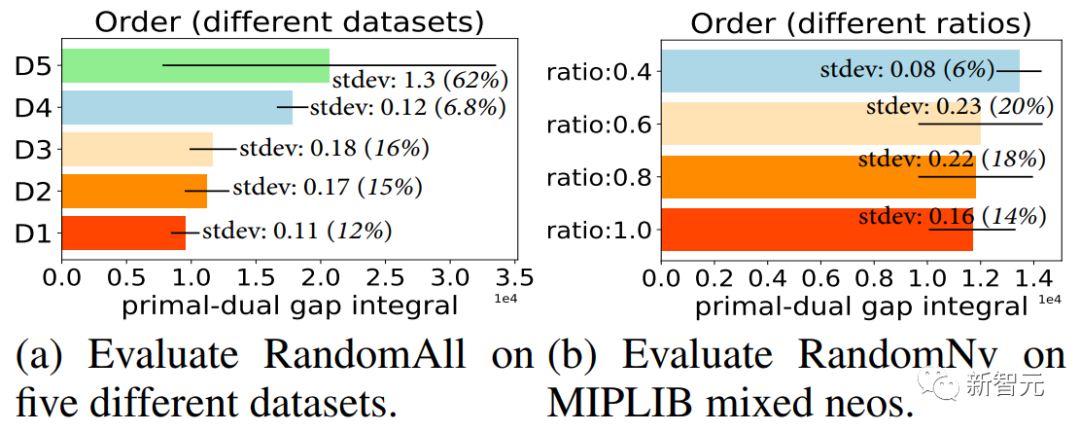
圖2. 每一個柱子代表在求解器中,選定相同的一批割平面,以10輪不同的順序添加這些選定割平面,求解器最終的求解效率的均值,柱子中的標準差線代表不同順序下求解效率的標準差。標準差越大,代表順序對求解器求解效率影響越大。
3 方法介紹
在割平面選擇任務中,應該選擇的最優子集是不可事先獲取的。
不過,我們可以使用求解器評估所選任意子集的質量,并以此評估作為學習算法的反饋。
因此,我們利用強化學習(Reinforcement Learning, RL)范式來試錯學習割平面選擇策略。
在本節中,我們詳細闡述了我們提出的 RL 框架。
首先,我們將割平面選擇任務建模為馬爾科夫決策過程(Markov Decision Process, MDP);然后,我們詳細介紹我們提出的分層序列模型(hierarchical sequence model, HEM);最后,我們推導可高效訓練 HEM 的分層策略梯度。我們整體的 RL 框架圖如圖3所示。
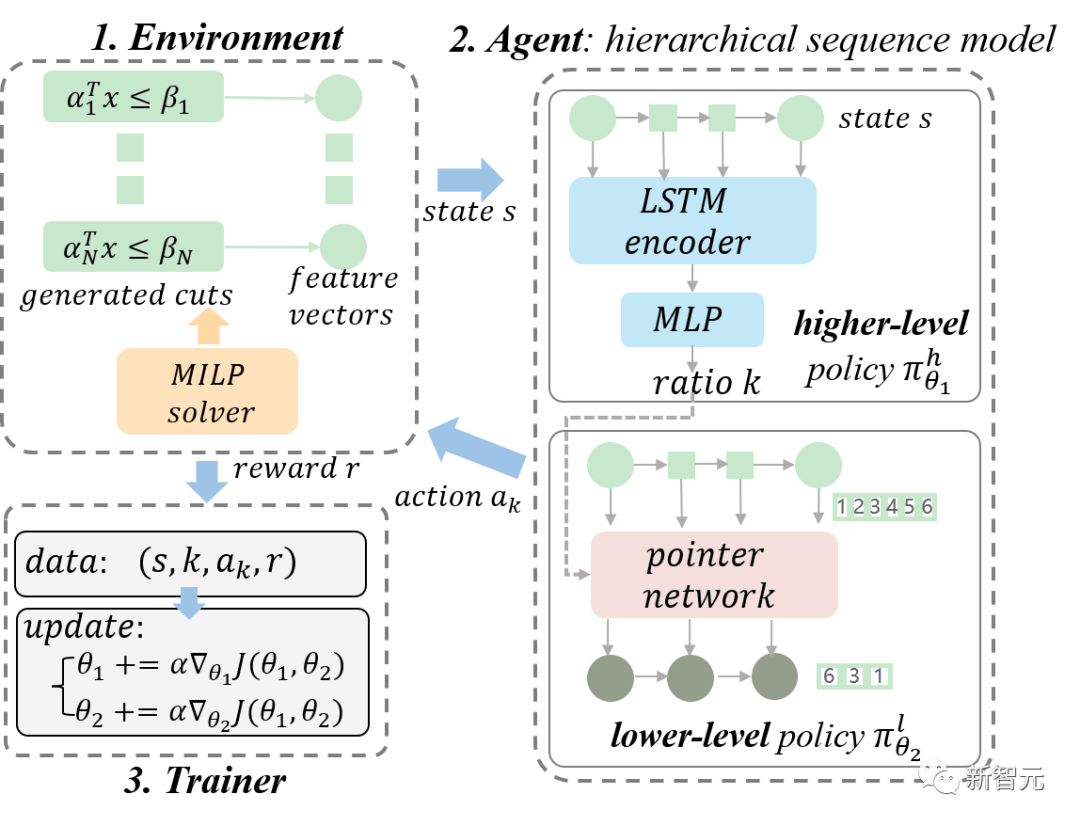
圖3. 我們所提出的整體 RL 框架圖。我們將 MILP 求解器建模為環境,將 HEM 模型建模為智能體。我們通過智能體和環境不斷交互采集訓練數據,并使用分層策略梯度訓練 HEM 模型。
3.1 問題建模
狀態空間:由于當前的 LP 松弛和生成的待選 cuts 包含割平面選擇的核心信息,我們通過定義狀態。這里 表示當前 LP 松弛的數學模型, 表示候選割平面的集合,表示 LP 松弛的最優解。為了編碼狀態信息,我們根據的信息為每個待選割平面設計13個特征。也就是說,我們通過一個13維特征向量來表示狀態 s。具體細節請見原文第4章節。
動作空間:為了同時考慮所選 cut 的比例和順序,我們以候選割平面集合的所有有序子集定義動作空間。
獎勵函數:為了評估添加 cut 對求解 MILP 的影響,我們可通過求解時間,原始對偶間隙積分(primal-dual gap integral),對偶界提升(dual bound improvement)。具體細節請見原文第4章節。
轉移函數:轉移函數給定當前狀態和采取的動作,輸出下一狀態。割平面選擇任務中轉移函數隱式地由求解器提供。
更多建模細節請見原文第4章節。
3.2 策略模型:分層序列模型
如圖3所示,我們將 MILP 求解器建模為環境,將 HEM 建模為智能體,下面詳細介紹所提出的 HEM 模型。為了方便閱讀,我們簡化方法動機,聚焦于講清楚方法實現,歡迎感興趣的讀者參見原論文第4章節,了解相關細節。
如圖3中 Agent 模塊所示,HEM 由上下層策略模型組成。上下層模型分別學習上層策略(policy) 和下層policy 。
首先,上層策略通過預測恰當的比例來學習應該選擇的 cuts 的數量。假設狀態長度為,預測比率為,那么預測應該選擇的 cut 數為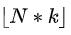
,其中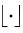 表示向下取整函數。我們定義
表示向下取整函數。我們定義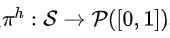 。
。
其次,下層策略學習選擇給定大小的有序子集。下層策略可以定義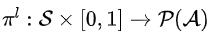 ,其中
,其中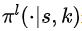 表示給定狀態S和比例K的動作空間上的概率分布。具體來說,我們將下層策略建模為一個序列到序列模型(sequence to sequence model, sequence model)。
表示給定狀態S和比例K的動作空間上的概率分布。具體來說,我們將下層策略建模為一個序列到序列模型(sequence to sequence model, sequence model)。
最后,通過全概率定律推導出 cut 選擇策略,即
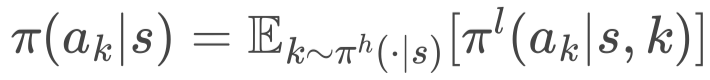
3.3 訓練方法:分層策略梯度
給定優化目標函數
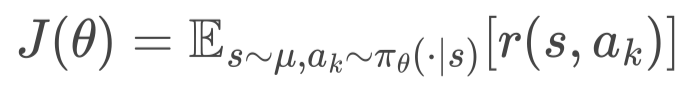
圖4. 分層策略梯度。我們以此隨機梯度下降的方式優化 HEM 模型。
4 實驗介紹
我們的實驗有五個主要部分:
實驗1. 在3個人工生成的MILP問題和來自不同應用領域的6個具有挑戰性的MILP問題基準上評估我們的方法。
實驗2. 進行精心設計的消融實驗,以提供對HEM的深入洞察。
實驗3. 測試 HEM 針對問題規模的泛化性能。
實驗4. 可視化我們的方法與基線所選擇的割平面特點。
實驗5. 將我們的方法部署到華為實際的排產規劃問題中,驗證 HEM 的優越性。
我們在此文章中只介紹實驗1,更多實驗結果,請參見原論文第5章節。請注意,我們論文中匯報的所有實驗結果都是基于 PyTorch 版本代碼訓練得到的結果。
實驗1結果如表1所示,我們在9個開源數據集上對比了 HEM 和6個基線的對比結果。實驗結果顯示,HEM 可平均提升約 20% 求解效率。
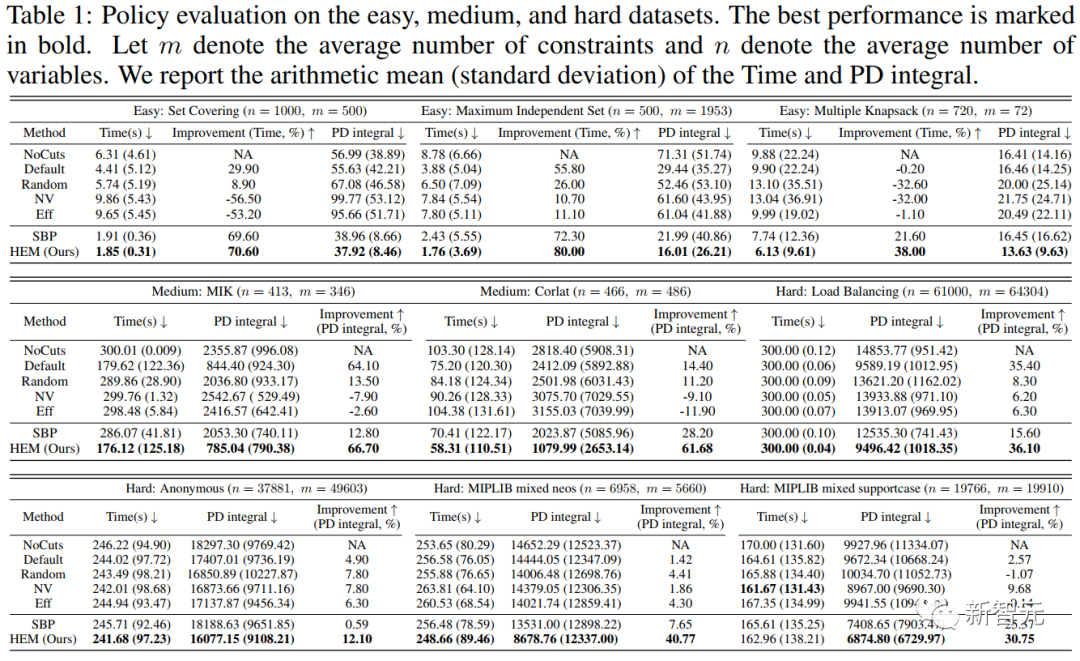
圖5. 對easy、medium 和 hard 數據集的策略評估。最優性能我們用粗體字標出。以m表示約束條件的平均數量,n表示變量的平均數量。我們展示了求解時間和primal-dual gap 積分的算術平均值(標準偏差)。










































