一篇學會樹的子結構
作者：神奇的程序員
在我的數據結構與算法實現系列文章——實現二叉搜索樹中，我們知道了二叉樹最多只能有兩個子節點：左子節點、右子節點。
前言
給定兩顆二叉樹A和B，如何判斷B是不是A的子結構，本文將分享一個方案用來解決此問題，歡迎各位感興趣的開發者閱讀本文。
思路分析
在我的數據結構與算法實現系列文章——實現二叉搜索樹中，我們知道了二叉樹最多只能有兩個子節點：左子節點、右子節點。那么，在本題中要判斷是否包含，可以分為兩步來實現：
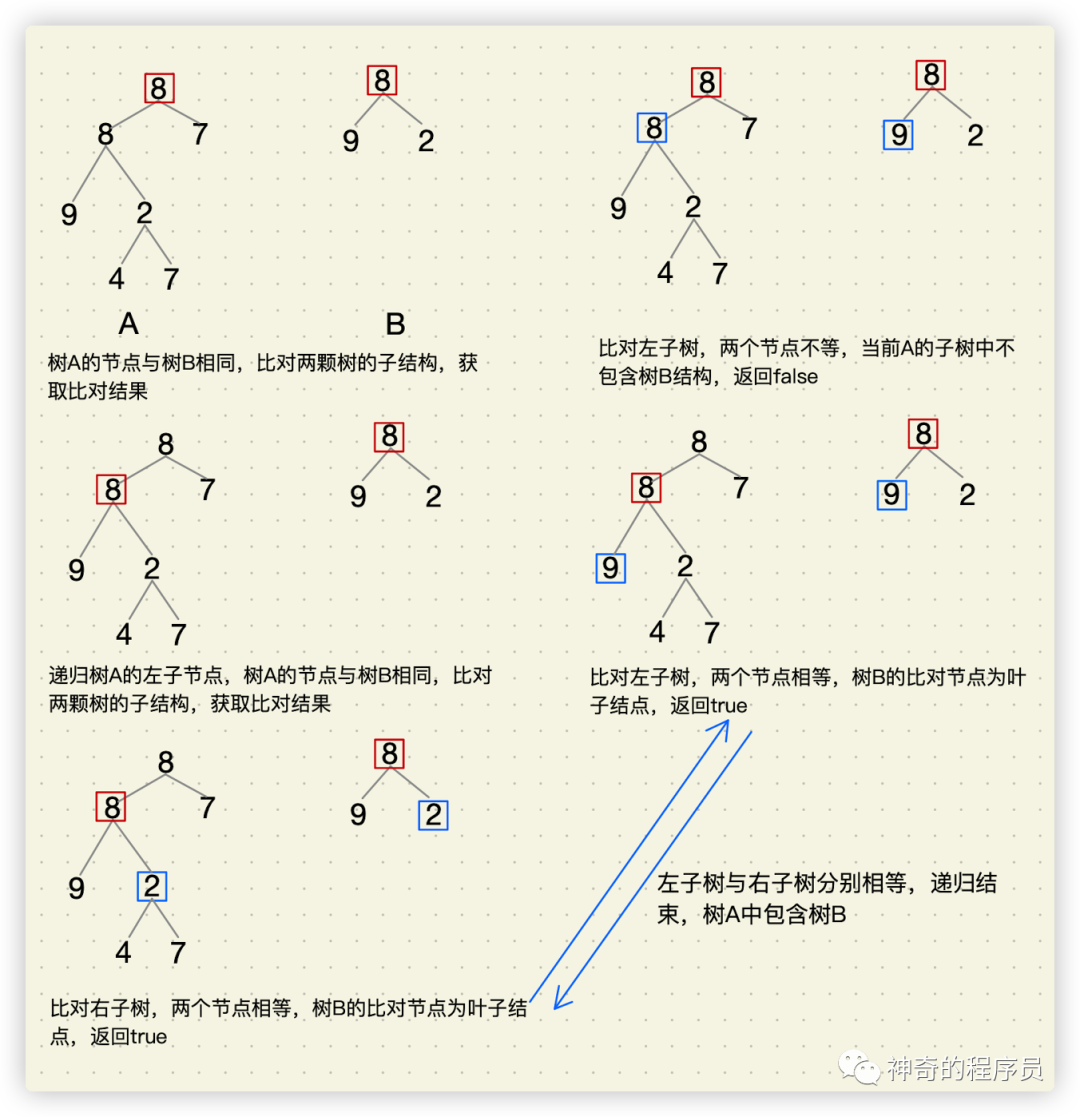
- 在樹A中找到和樹B的根節點的值一樣的節點R
如果樹A的節點與樹B的根結點相同，則執行進一步的判斷（比對兩棵樹的子結構）得出比對結果
如果得出的結果為false，分別遞歸樹A的左子節點與右子節點跟樹B進行比對，直至任意一棵樹的葉子節點
- 判斷樹A中以R為根節點的子樹是否包含和樹B一樣的結構
如果樹B為null則代表樹A中包含樹B，返回true
如果樹A為null則代表樹A中不包含樹B，返回false
如果比對的兩個節點不等，則代表當前A的子樹中不包含樹B結構，返回false
否則，繼續執行遞歸，直至任意一棵樹的葉子節點
實現代碼
通過上個章節的分析，我們已經得出了具體的思路，接下來，我們就將思路轉換為代碼，如下所示：
實現主函數，判斷B是否為A的子結構：
遞歸樹A將其與樹B的節點進行比對，找到相同的節點再做進一步的比對
export function TreeSubstructure(
treeA: BinaryTreeNode | null | undefined,
treeB: BinaryTreeNode | null | undefined
): boolean {
let result = false;
if (treeA != null && treeB != null) {
// 兩個節點相同
if (treeA.key === treeB.key) {
// 判斷樹A中是否包含樹B
result = treeAHaveTreeB(treeA, treeB);
}
// 繼續尋找左子樹與右子樹
if (!result) {
result = TreeSubstructure(treeA?.left, treeB);
}
if (!result) {
result = TreeSubstructure(treeA?.right, treeB);
}
}
return result;
}
- 實現進一步的比對函數，判斷樹A的子節點中是否包含跟樹B一樣的結構
function treeAHaveTreeB(
treeA: BinaryTreeNode | null | undefined,
treeB: BinaryTreeNode | null | undefined
): boolean {
// 遞歸到了樹B的葉節點，代表該節點存在于樹A中
if (treeB == null) {
return true;
}
// 遞歸到樹A的葉節點，代表該節點不存在于樹A中
if (treeA == null) {
return false;
}
if (treeA.key !== treeB.key) {
return false;
}
// 左子樹與右子樹都相同
return (
treeAHaveTreeB(treeA?.left, treeB?.left) &&
treeAHaveTreeB(treeA?.right, treeB?.right)
);
}
注意：上述代碼中用到了遞歸，如果你對其不了解，可以移步我的另一篇文章：遞歸的理解與實現
代碼中還用到了一個自定義類型BinaryTreeNode，具體的類型定義請移步示例代碼章節。
測試用例
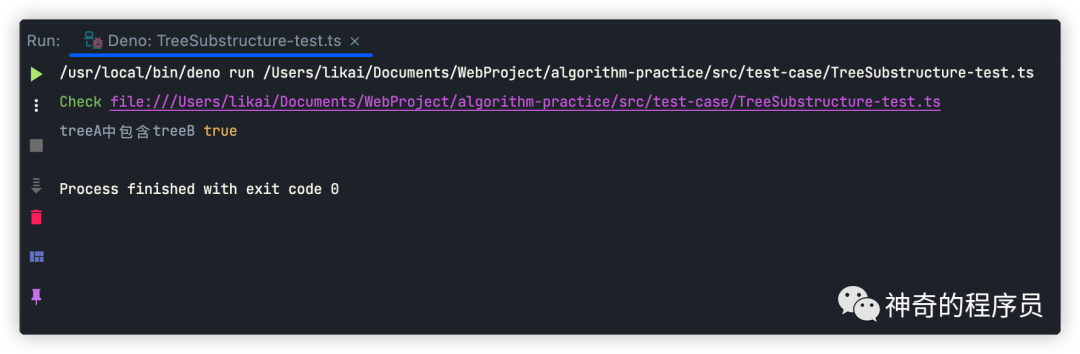
接下來，我們用思路分析章節中所舉的例子來測試下上述函數能否正確執行。
const treeA: BinaryTreeNode = {
key: 8,
left: {
key: 8,
left: { key: 9 },
right: { key: 2, left: { key: 4 }, right: { key: 7 } }
},
right: { key: 7 }
};
const treeB: BinaryTreeNode = {
key: 8,
left: {
key: 9
},
right: {
key: 2
}
};
const result = TreeSubstructure(treeA, treeB);
console.log("treeA中包含treeB", result);
示例代碼
本文所用代碼完整版請移步：
- TreeSubstructure.ts
- TreeSubstructure-test
責任編輯：武曉燕
來源：
神奇的程序員
