一篇學會檢測循環依賴
本文轉載自微信公眾號「一個搬磚的胖子」,作者一個搬磚的胖子。轉載本文請聯系一個搬磚的胖子公眾號。
前言
今天為CodeTop補充的題目是檢測循環依賴。
來看一下幾篇面經的原文敘述
- 循環依賴檢測。如,[['A', 'B'], ['B', 'C'], ['C', 'D'], ['B', 'D']] => false,[['A', 'B'], ['B', 'C'], ['C', 'A']] => true(2021.4 字節跳動-幸福里-后端)[2]
- 手撕代碼:小王寫了一個makefile,其中有n個編譯項編號為0~n-1,他們互相之間有依賴關系。請寫一個程序解析依賴,給出一個可行的編譯順序。(2021.03 字節跳動-系統部-后端)[3]
有的面試官要求判斷是否有循環依賴;有的則要求給出一個可行的順序。
解決這類問題的利器就是——拓撲排序。
只要你會BFS,會層次遍歷二叉樹。
你很快就能掌握拓撲排序的寫法。
題目描述
現有n個編譯項,編號為0 ~ n-1。給定一個二維數組,表示編譯項之間有依賴關系。如[0, 1]表示1依賴于0。
若存在循環依賴則返回空;不存在依賴則返回可行的編譯順序。
題目分析
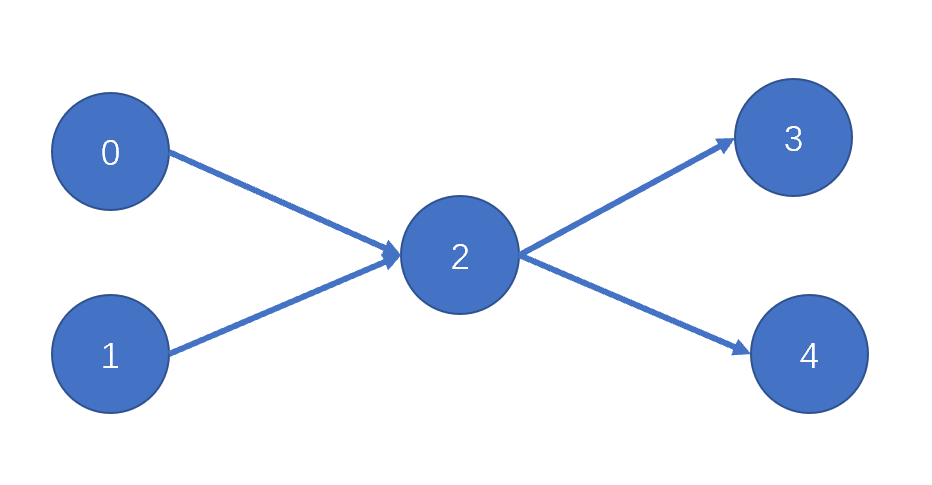
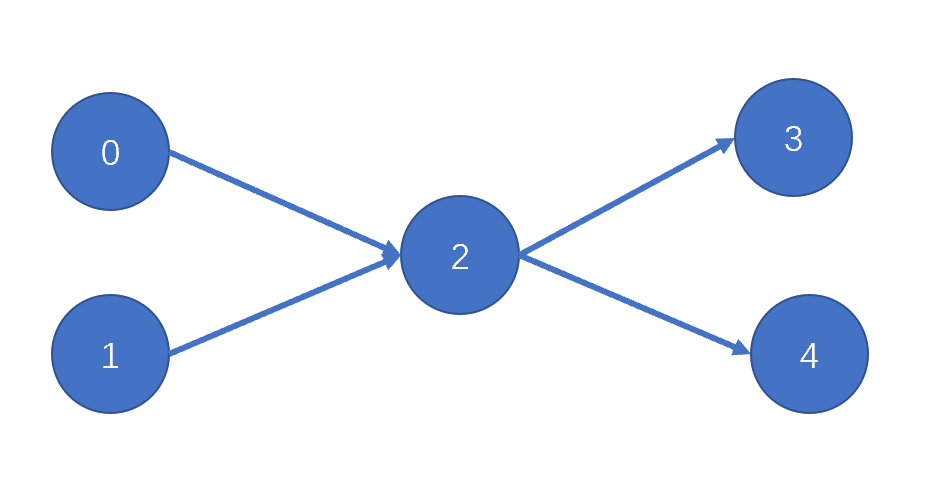
若給定一個依賴關系是[[0,2],[1,2],[2,3],[2,4]],如圖所示
可以看出,它們之間不存在循環依賴。
可行的編譯序列是[0,1,2,3,4],也可以是[1,0,2,4,3]等。
拓撲排序可以求這樣的一個序列。可以看出,這個序列結果可能不唯一。
拓撲排序算法過程:
- 選擇圖中一個入度為0的點,記錄下來
- 在圖中刪除該點和所有以它為起點的邊
- 重復1和2,直到圖為空或沒有入度為0的點。
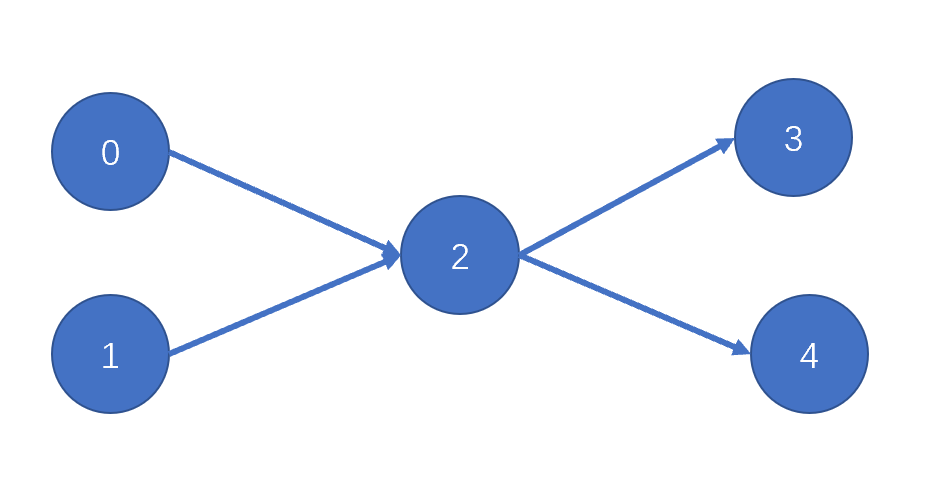
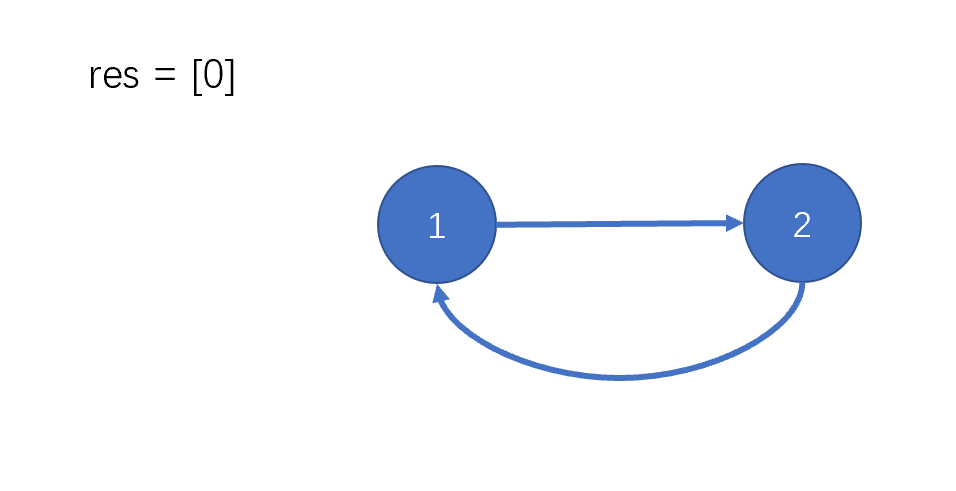
用下圖舉個例子,看看拓撲排序算法的過程。res用于存儲結果序列。
圖片入度為0的點有兩個,我們任選一個。比如選擇點0,記錄至res;刪除點0及以它為起點的邊。
然后選擇點1,同樣記錄下來;刪除點1及以它為起點的邊。
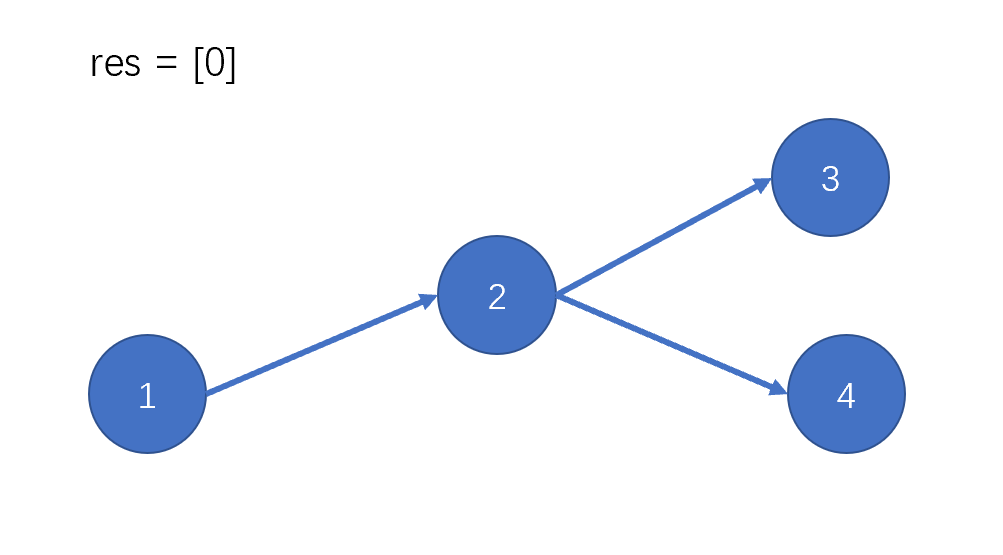
入度為0的點現在只有點2,把它記錄下來;刪除點2及以它為起點的邊。
同理。選擇點3,記錄下來;刪除點3及以它為起點的邊。
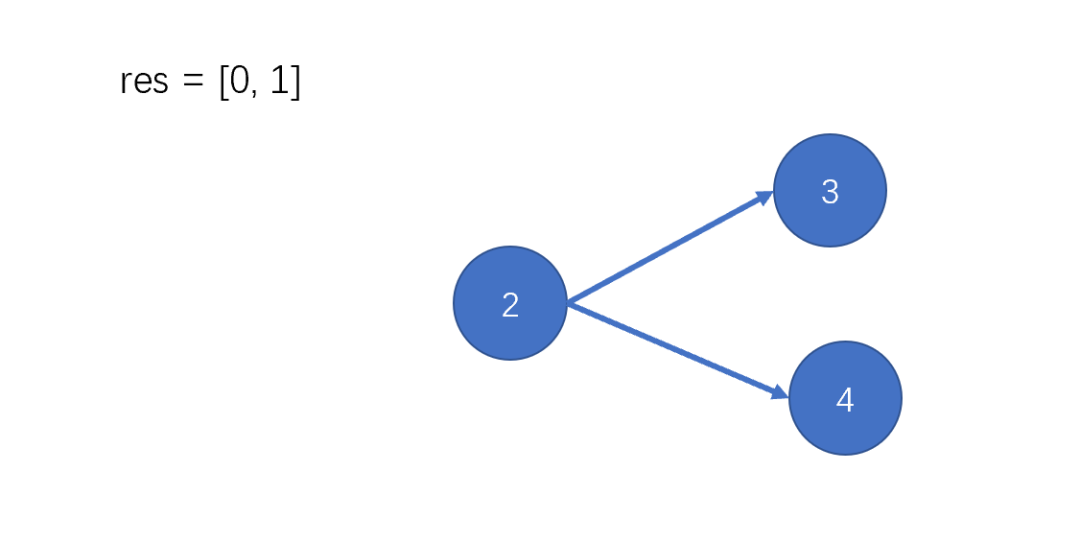
選擇點4,記錄下來;刪除點4及以它為起點的邊。
圖為空,算法結束。
最終,res存儲的就是拓撲排序的結果,即題目中的可行編譯順序。
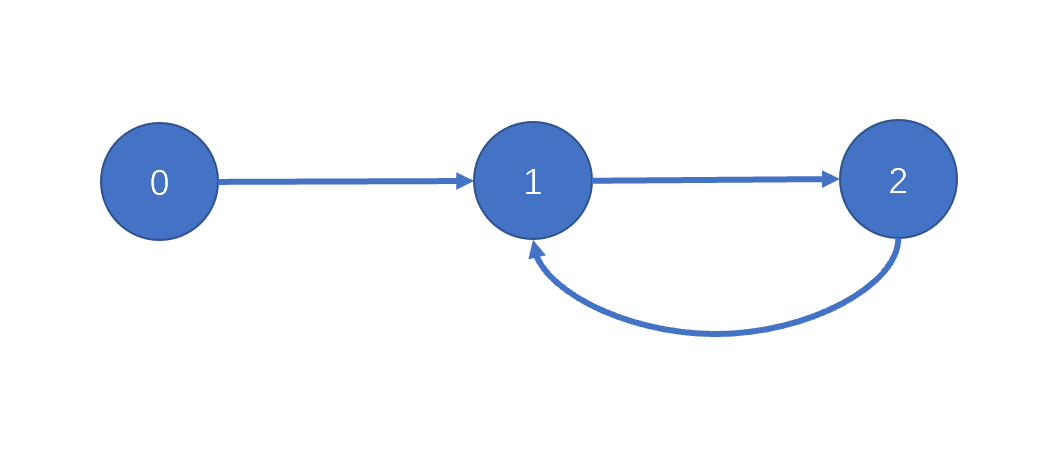
如果圖中存在循環依賴呢?
例如依賴關系是[[0,1],[1,2],[2,1],如圖所示。
按照拓撲排序的算法,找到入度為0的點0存下來,然后刪除。
然后就沒有入度為0的點了,算法結束!
我們發現,可以使用res.size() == n 來判斷圖中是否有環。其中,n為點的個數。
這就是拓撲排序算法。
代碼實現應該就很好理解了~我們借助BFS來實現拓撲排序,隊列中存儲入度為0的點。
下面我提供C++和Python兩個版本的代碼。推薦大家背下來,背一些模板代碼是很有必要的。
如果你感覺拓撲排序沒問題了,去嘗試做Leetcode210. 課程表 II吧~
PS:之前沒接觸過圖的同學,可能不太理解參考代碼中存儲圖結構的g。其實很簡單,對于下圖來說。
- g = [[2] #表示0->2
- [2] #表示1->2
- [3, 4] #表示2->3,2->4
- [] #表示沒有以3為起點的邊
- []] #表示沒有以4為起點的邊
參考代碼
C++ 版本
- vector<int> haveCircularDependency(int n, vector<vector<int>> &prerequisites) {
- vector<vector<int>> g(n); //鄰接表存儲圖結構
- vector<int> indeg(n); //每個點的入度
- vector<int> res; //存儲結果序列
- for(int i = 0; i < prerequisites.size(); i ++) {
- int a = prerequisites[i][0], b = prerequisites[i][1];
- g[a].push_back(b);
- indeg[b] ++;
- }
- queue<int> q;
- //一次性將入度為0的點全部入隊
- for(int i = 0; i < n; i ++) {
- if(indeg[i] == 0) q.push(i);
- }
- while(q.size()) {
- int t = q.front();
- q.pop();
- res.push_back(t);
- //刪除邊時,將終點的入度-1。若入度為0,果斷入隊
- for(int i = 0; i < g[t].size(); i ++) {
- int j = g[t][i];
- indeg[j] --;
- if(indeg[j] == 0) {
- q.push(j);
- }
- }
- }
- if(res.size() == n) return res;
- else return {};
- }
Python 版本
- def haveCircularDependency(self, n: int, prerequisites):
- g = [[]for i in range(n)] #鄰接表存儲圖結構
- indeg = [0 for i in range(n)] #每個點的入度
- res = [] #存儲結果序列
- q = deque()
- #將依賴關系加入鄰接表中g,并各個點入度
- for pre in prerequisites:
- a, b = pre[0], pre[1]
- g[a].append(b)
- indeg[b] += 1
- #一次性將入度為0的點全部入隊
- for i in range(n):
- if indeg[i] == 0:
- q.append(i)
- while q:
- t = q.popleft()
- res.append(t)
- #刪除邊時,將終點的入度-1。若入度為0,果斷入隊
- for j in g[t]:
- indeg[j] -= 1
- if indeg[j] == 0:
- q.append(j)
- if len(res) == n:
- return res
- else:
- return []