01 前言

該論文是關(guān)于深度強(qiáng)化學(xué)習(xí)對抗攻擊的工作。在該論文中，作者從魯棒優(yōu)化的角度研究了深度強(qiáng)化學(xué)習(xí)策略對對抗攻擊的魯棒性。在魯棒優(yōu)化的框架下，通過最小化策略的預(yù)期回報來給出最優(yōu)的對抗攻擊，相應(yīng)地，通過提高策略應(yīng)對最壞情況的性能來實現(xiàn)良好的防御機(jī)制。

考慮到攻擊者通常無法 在訓(xùn)練環(huán)境中 攻擊，作者提出了一種貪婪攻擊算法，該算法試圖在不與環(huán)境交互的情況下最小化策略的預(yù)期回報；另外作者還提出一種防御算法，該算法以最大-最小的博弈來對深度強(qiáng)化學(xué)習(xí)算法進(jìn)行對抗訓(xùn)練。

在Atari游戲環(huán)境中的實驗結(jié)果表明，作者提出的對抗攻擊算法比現(xiàn)有的攻擊算法更有效，策略回報率更差。論文中提出的對抗防御算法生成的策略比現(xiàn)有的防御方法對一系列對抗攻擊更具魯棒性。

02 預(yù)備知識

2.1對抗攻擊

給定任何一個樣本(x,y)和神經(jīng)網(wǎng)絡(luò)f，生成對抗樣本的優(yōu)化目標(biāo)為：

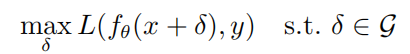
其中 是神經(jīng)網(wǎng)絡(luò)f的參數(shù)，L是損失函數(shù)， 是對抗擾動集合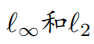， 是以x為中心， 為半徑的范數(shù)約束球。通過PGD攻擊生成對抗樣本的計算公式如下所示：

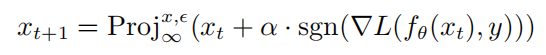
其中 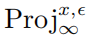表示的是投影操作，如果輸入在范數(shù)球外，則將輸入投影到以x中心， 為半徑的 球上， 表示的是PGD攻擊的單步擾動大小。

2.2強(qiáng)化學(xué)習(xí)和策略梯度

一個強(qiáng)化學(xué)習(xí)問題可以被描述為一個馬爾可夫決策過程。馬爾可夫決策過程又可以被定義為一個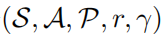的五元組，其中S表示的是一個狀態(tài)空間，A表示的是一個動作空間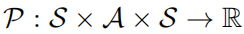，表示的是狀態(tài)轉(zhuǎn)移概率，r表示的是獎勵函數(shù)， 表示的是折扣因子。強(qiáng)學(xué)學(xué)習(xí)的目標(biāo)是去學(xué)習(xí)一個參數(shù)策略分布 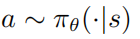使得價值函數(shù)最大化

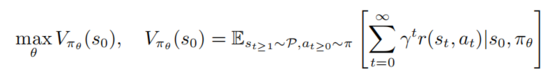
其中 表示的是初始狀態(tài)。強(qiáng)學(xué)學(xué)習(xí)包括評估動作值函數(shù)

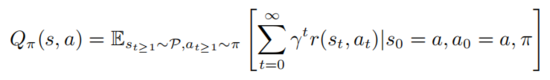
以上公式描述了在狀態(tài) 執(zhí)行 后服從策略 的數(shù)學(xué)期望。由定義可知值函數(shù)和動作值函數(shù)滿足如下關(guān)系：

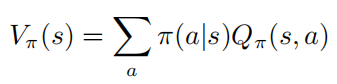
為了便于表示，作者主要關(guān)注的是離散動作空間的馬爾可夫過程，但是所有的算法和結(jié)果都可以直接應(yīng)用于連續(xù)的設(shè)定。

03 論文方法

深度強(qiáng)化學(xué)習(xí)策略的對抗攻擊和防御是建立在是魯棒優(yōu)化PGD的框架之上的

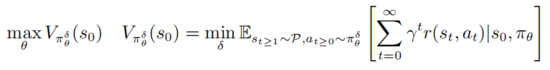
其中 表示的是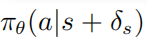， 表示的是對抗擾動序列集合 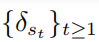，并且對于所有的  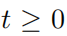，滿足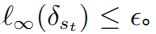以上公式提供了一個深度強(qiáng)化學(xué)習(xí)對抗攻擊和防御的統(tǒng)一框架。

一方面內(nèi)部最小化優(yōu)化去尋找對抗擾動序列 使得當(dāng)前策略 做出錯誤的決策。另一方面外部最大化的目的是找到策略分布參數(shù) 使得在擾動策略下期望回報最大。經(jīng)過以上對抗攻擊和防御博弈，會使得訓(xùn)練過程中的策略參數(shù) 能夠更加抵御對抗攻擊。

目標(biāo)函數(shù)內(nèi)部最小化的目的是生成對抗擾動 ，但是對于強(qiáng)化學(xué)習(xí)算法來說學(xué)習(xí)得到最優(yōu)對抗擾動是非常耗時耗力的，而且由于訓(xùn)練環(huán)境對攻擊者來說是一個黑盒的，所以在該論文中，作者考慮一個實際的設(shè)定，即攻擊者在不同的狀態(tài)下去注入擾動。不想有監(jiān)督學(xué)習(xí)攻擊場景中，攻擊者只需要欺騙分類器模型使得它分類出錯產(chǎn)生錯誤的標(biāo)簽；在強(qiáng)化學(xué)習(xí)的攻擊場景中，動作值函數(shù)攻擊者提供了額外的信息，即小的行為值會導(dǎo)致一個小的期望回報。相應(yīng)的，作者在深度強(qiáng)化學(xué)習(xí)中定義了最優(yōu)對抗擾動如下所示

定義1： 一個在狀態(tài)s上最優(yōu)的對抗擾動 能夠最小化狀態(tài)的期望回報

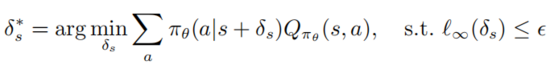
需要注意的是優(yōu)化求解以上公式的是非常棘手的，它需要確保攻擊者能夠欺騙智能體使得其選擇最差的決策行為，然而對于攻擊者來說智能體的動作值函數(shù)是不可知的，所以無法保證對抗擾動是最優(yōu)的。以下的定理能夠說明如果策略是最優(yōu)的，最優(yōu)對抗擾動能夠用不通過訪問動作值函數(shù)的方式被生成

定理1： 當(dāng)控制策略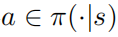是最優(yōu)的，動作值函數(shù)和策略滿足以下關(guān)系

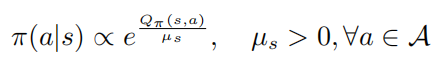
其中 表示的是策略熵， 是一個狀態(tài)依賴常量，并且當(dāng) 變化到0的時候， 也會隨之變?yōu)?，進(jìn)而則有以下公式

證明： 當(dāng)隨機(jī)策略 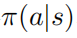 達(dá)到最優(yōu)的時候，值函數(shù)  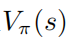也達(dá)到了最優(yōu)，這也就是說，在每個狀態(tài)s下，找不到任何其它的行為分布使得值函數(shù)  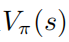增大。相應(yīng)的，給定最優(yōu)的動作值函數(shù)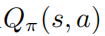，可以通過求解約束優(yōu)化問題獲得最優(yōu)策略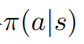

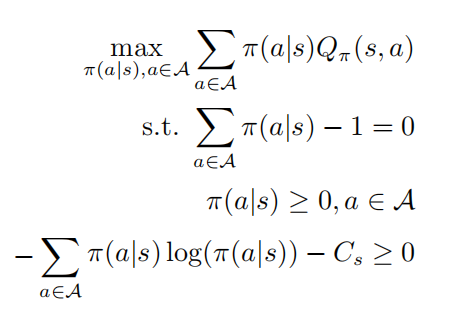
其中第二和第三行表示 是一個概率分布，最后一行表示策略 是一個隨機(jī)策略，根據(jù)KKT條件則可以將以上優(yōu)化問題轉(zhuǎn)化為如下形式：

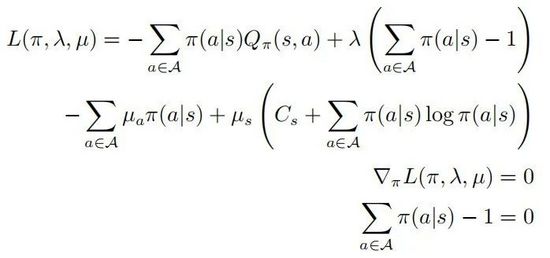
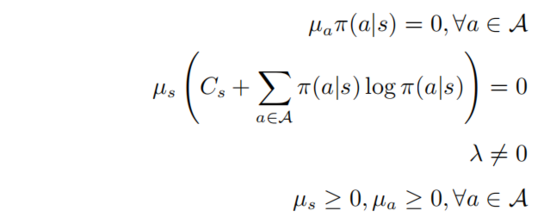
其中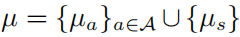。假定 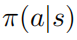 對于所有的行為  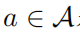是正定的，則有：

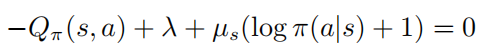
當(dāng) 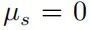，則必有 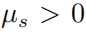，進(jìn)而則有對于任意的 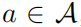，則有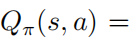從而會得到動作值函數(shù)和策略的softmax的關(guān)系

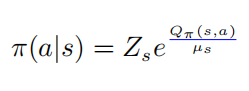
其中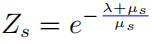，進(jìn)而有

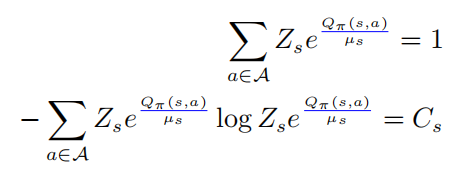
將以上的第一個等式帶入到第二中，則有

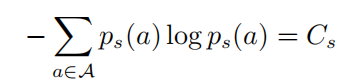
其中

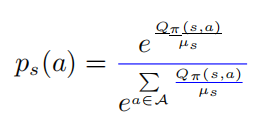
以上公式中 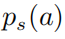 表示的是一個softmax形式的概率分布，并且它的熵等于 。當(dāng) 等于0的時候， 也變?yōu)?.在這種情況下， 是要大于0的，則此時。

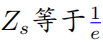定理1展示了如果策略是最優(yōu)的情況下，最優(yōu)擾動可以通過最大化擾動策略和原始策略的交叉熵來獲得。為了討論的簡便，作者將定理1的攻擊稱之為策略攻擊，而且作者使用PGD算法框架去計算最優(yōu)的策略攻擊，具體的算法流程圖如下算法1所示。

作者提出的防御對抗擾動的魯棒優(yōu)化算法的流程圖如下算法2所示，該算法被稱之為策略攻擊對抗訓(xùn)練。在訓(xùn)練階段，擾動策略 被用作去和環(huán)境交互，與此同時擾動策略的動作值函數(shù)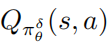被估計去幫助策略訓(xùn)練。

具體的細(xì)節(jié)為，首先在訓(xùn)練階段作者使用策略攻擊去生成擾動，即使值函數(shù)沒有保證被減小。在訓(xùn)練的早期階段，策略也許跟動作值函數(shù)不相關(guān)，隨著訓(xùn)練的進(jìn)行，它們會慢慢滿足softmax 的關(guān)系。

另一方面作者需要精確評估動作值函數(shù)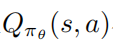很難處理，因為軌跡是通過運行受干擾的策略收集的，而使用這些數(shù)據(jù)估計未受干擾策略的作用值函數(shù)可能非常不準(zhǔn)確。

使用PPO的優(yōu)化擾動策略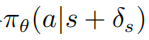的目標(biāo)函數(shù)為

其中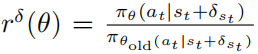，并且 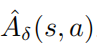是擾動策略平均函數(shù)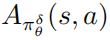的一個估計。在實際中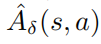，是由方法GAE估計得來的。具體的算法流程圖如下圖所示。

 04 實驗結(jié)果

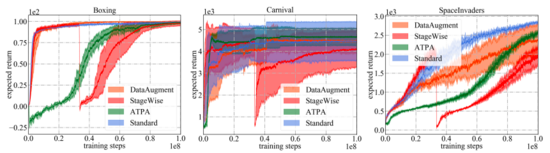
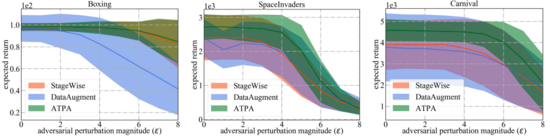
如下右側(cè)的三個子圖顯示了不同攻擊擾動的結(jié)果。可以發(fā)現(xiàn)經(jīng)過逆向訓(xùn)練的策略和標(biāo)準(zhǔn)策略都能抵抗隨機(jī)擾動。相反，對抗攻擊會降低不同策略的性能。結(jié)果取決于測試環(huán)境和防御算法，進(jìn)一步可以發(fā)現(xiàn)三種對抗性攻擊算法之間的性能差距很小。

相比之下，在相對困難的設(shè)置環(huán)境中，論文作者提出的策略攻擊算法干擾的策略產(chǎn)生的回報要低得多。總體而言，論文中提出的策略攻擊算法在大多數(shù)情況下產(chǎn)生的回報最低，這表明它確實是所有經(jīng)過測試的對抗攻擊算法中效率最高的。

如下圖所示顯示了不同防御算法以及標(biāo)準(zhǔn)PPO的學(xué)習(xí)曲線。需要注意的是性能曲線僅表示用于與環(huán)境交互的策略的預(yù)期回報。在所有的訓(xùn)練算法中，論文中提出的ATPA具有最低的訓(xùn)練方差，因此比其他算法更穩(wěn)定。另外還能注意到，ATPA的進(jìn)度比標(biāo)準(zhǔn)PPO慢得多，尤其是在早期訓(xùn)練階段。這導(dǎo)致了這樣一個事實，即在早期的訓(xùn)練階段，受不利因素干擾會使得策略訓(xùn)練非常不穩(wěn)定。

表總結(jié)了使用不同算法在不同擾動下的策略預(yù)期回報。可以發(fā)現(xiàn)經(jīng)過ATPA訓(xùn)練的策略能夠抵抗各種對抗干擾。相比之下，盡管StageWise和DataAugment在某種程度上學(xué)會了處理對抗攻擊，但它們在所有情況下都不如ATPA有效。

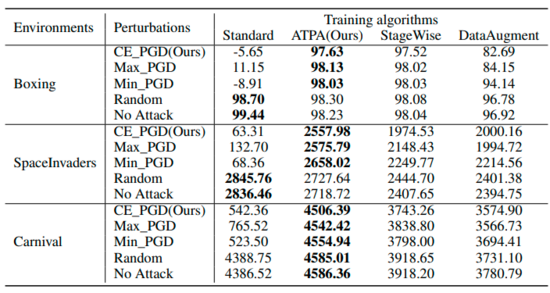
為了進(jìn)行更廣泛的比較，作者還評估了這些防御算法對最有效的策略攻擊算法產(chǎn)生的不同程度的對抗干擾的魯棒性。如下圖所示，ATPA再次在所有情況下獲得最高分?jǐn)?shù)。此外，ATPA的評估方差遠(yuǎn)小于StageWise和DataAugment，表明ATPA具有更強(qiáng)的生成能力。

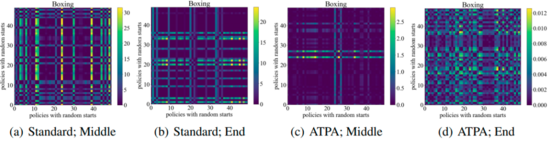
為了達(dá)到類似的性能，ATPA需要比標(biāo)準(zhǔn)PPO算法更多的訓(xùn)練數(shù)據(jù)。作者通過研究擾動策略的穩(wěn)定性來深入研究這個問題。作者計算了通過在訓(xùn)練過程中間和結(jié)束時使用不同隨機(jī)初始點的PGD執(zhí)行策略攻擊而獲得的擾動策略的KL散度值。如下圖所示，在沒有對抗訓(xùn)練的情況下，即使標(biāo)準(zhǔn)PPO已經(jīng)收斂，也會不斷觀察到較大的KL 散度值，這表明策略對于使用不同初始點執(zhí)行PGD所產(chǎn)生的擾動非常不穩(wěn)定。

下圖顯示了具有不同初始點的擾動策略的KL散度圖，可以發(fā)現(xiàn)圖中的每個像素表示兩個擾動策略的KL散度值，這兩個擾動策略通過最大化ATPA算法的核心公式給出。需要注意的是由于KL散度是一個非對稱度量，因此這些映射也是不對稱的。

? ?