在之前對(duì)序列模型中的??HMM(隱馬爾可夫模型)??進(jìn)行掌握以后，有必要對(duì)另外一個(gè)序列模型CRF進(jìn)行掌握，因?yàn)檫@兩個(gè)模型都是自然語(yǔ)言處理序列模型中的核心模型。在之前介紹的概率有向圖模型，如HMM，即貝葉斯網(wǎng)絡(luò)，相對(duì)應(yīng)的概率無(wú)向圖模型就稱為馬爾可夫網(wǎng)絡(luò)或者馬爾可夫隨機(jī)場(chǎng)(MRF)，本篇文章所介紹的CRF就是馬爾可夫隨機(jī)場(chǎng)的一種。

1.馬爾可夫隨機(jī)場(chǎng)

馬爾可夫隨機(jī)場(chǎng)也叫馬爾可夫網(wǎng)絡(luò)，同時(shí)也是一種無(wú)向圖模型。在概率圖模型的基礎(chǔ)上，針對(duì)無(wú)向圖模型，首先需要對(duì)無(wú)向圖模型的基礎(chǔ)概念進(jìn)行一定程度上的掌握。

1.1. MRF相關(guān)概念

無(wú)向圖模型MRF所特有的一些概念如下：

• 團(tuán)：圖中的節(jié)點(diǎn)子集，并且其中任意兩個(gè)節(jié)點(diǎn)之間都有邊連接;
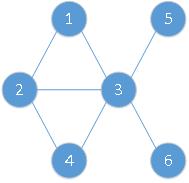
• 極大團(tuán)：為一個(gè)團(tuán)，并且加入任何一個(gè)其他的節(jié)點(diǎn)都不能再形成團(tuán)，例如下圖中，該圖中的團(tuán)一共有{1,2}，{1,3}，{2,3}，{2,4}，{3,4}，{3,5}，{3,6}，{1,3}，{1,2,3}，{2,3,4};其中極大團(tuán)為{1,2,3}，{2,3,4}，{3,5}，{3,6};

• 勢(shì)函數(shù)(也稱因子Factor)：定義在變量子集上的非負(fù)實(shí)函數(shù)，用于定義概率分布函數(shù)。在馬爾可夫隨機(jī)場(chǎng)中，多個(gè)變量之間的聯(lián)合概率分布可以基于團(tuán)分解為多個(gè)勢(shì)函數(shù)的乘積，每個(gè)勢(shì)函數(shù)僅僅與一個(gè)團(tuán)相關(guān)。
• 特征函數(shù)：通常情況下都是一些實(shí)數(shù)值函數(shù)，它是用來(lái)刻畫數(shù)據(jù)的一些可能成立的經(jīng)驗(yàn)特性。例如下式就是一個(gè)特征函數(shù)：

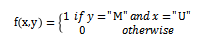
1.2. Hammersley-Clifford定理

在對(duì)于勢(shì)函數(shù)與團(tuán)相關(guān)理論掌握的基礎(chǔ)上，由此引申出隨機(jī)場(chǎng)的基礎(chǔ)定理，即Hammersley-Clifford定理。該定理的具體定義為：對(duì)于具有N個(gè)變量的馬爾可夫隨機(jī)場(chǎng)，已知變量為 ),這些變量中所有團(tuán)所構(gòu)成的集合為T，同時(shí)與團(tuán) 對(duì)應(yīng)的變量集合記作 ，則其對(duì)應(yīng)的聯(lián)合概率為：

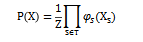
上式中， 就是與團(tuán)S所對(duì)應(yīng)的勢(shì)函數(shù)，其作用為對(duì)團(tuán) 中的變量關(guān)系進(jìn)行建模。 為規(guī)范化因子，其難以計(jì)算，在普遍情況下，無(wú)需計(jì)算出 的精確值。在針對(duì)于團(tuán) 不是極大團(tuán)的情況時(shí)，由于非極大團(tuán)必定屬于某個(gè)極大團(tuán)的性質(zhì)，所以還是可以用極大團(tuán)進(jìn)行計(jì)算來(lái)替代非極大團(tuán)的聯(lián)合概率，即:

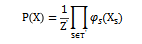
上式中的 就是所有極大團(tuán)的集合。Hammersley-Clifford定理是隨機(jī)場(chǎng)的基礎(chǔ)定理，其為馬爾可夫隨機(jī)場(chǎng)被表達(dá)為正概率分布的充分必要條件。針對(duì)于1.1中的示例圖，其聯(lián)合概率就為：

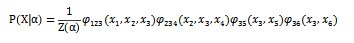
1.3. 分離集與馬爾科夫性

在對(duì)各種馬爾可夫性進(jìn)行掌握前，首先需要理解分離集的概念。分離集的定義為：設(shè)A、B、C都是馬爾可夫隨機(jī)場(chǎng)中的節(jié)點(diǎn)集合，如果從集合A中的節(jié)點(diǎn)到集合C中的節(jié)點(diǎn)都必須要經(jīng)過(guò)集合B中的節(jié)點(diǎn)，那么就可以稱集合A和集合C被集合B給分離，其中集合B就為分離集。如下圖所示：

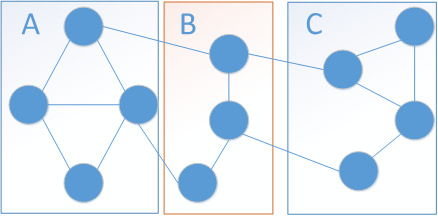
有了分離集合的概念，對(duì)下面幾種馬爾可夫性的理解就相對(duì)簡(jiǎn)單了，馬爾可夫性的定義為：當(dāng)一個(gè)隨機(jī)過(guò)程在給定當(dāng)前狀態(tài)及所有過(guò)去狀態(tài)情況下，其未來(lái)狀態(tài)的條件概率分布僅依賴于當(dāng)前狀態(tài)，即只要給定了當(dāng)前狀態(tài)，未來(lái)狀態(tài)是與過(guò)去狀態(tài)無(wú)關(guān)的，也是條件獨(dú)立的，該隨機(jī)過(guò)程也就具有了馬爾可夫性。同理，在馬爾可夫隨機(jī)場(chǎng)中，馬爾可夫性可解釋為當(dāng)前狀態(tài)看作為無(wú)向圖中的一個(gè)節(jié)點(diǎn)，過(guò)去狀態(tài)就是與當(dāng)前狀態(tài)節(jié)點(diǎn)有邊連接的其他節(jié)點(diǎn)。針對(duì)于馬爾可夫性和下圖，又有：

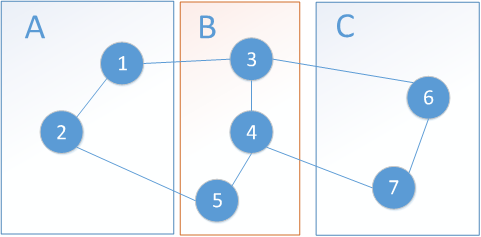
• 全局馬爾可夫性：節(jié)點(diǎn)集合A，C是無(wú)向圖中被節(jié)點(diǎn)集合B分開的任意結(jié)點(diǎn)集合，則在給定隨機(jī)變量Y_B的條件下，隨機(jī)變量Y_A和Y_C條件獨(dú)立。如上圖中節(jié)點(diǎn)1,2就與節(jié)點(diǎn)6,7條件獨(dú)立。
• 局部馬爾可夫性：設(shè)X是無(wú)向圖中任意一個(gè)結(jié)點(diǎn)，T是與X有邊相連的所有結(jié)點(diǎn)，無(wú)向圖中其他剩余結(jié)點(diǎn)為S，則給定隨機(jī)變量Y_T的條件下，隨機(jī)變量Y_X和Y_S條件獨(dú)立。如上圖的節(jié)點(diǎn)2，與2連接的節(jié)點(diǎn)為1和5，即給定節(jié)點(diǎn)1和5的情況下，那么節(jié)點(diǎn)2就與剩下的節(jié)點(diǎn)3，4，6，7條件獨(dú)立。
• 成對(duì)馬爾可夫性：設(shè)無(wú)向圖中V和C是任意兩個(gè)沒(méi)有邊直接連接的結(jié)點(diǎn)，圖中其他結(jié)點(diǎn)的集合記做S，則給定隨機(jī)變量Y_S的條件下，隨機(jī)變量Y_V和Y_C條件獨(dú)立。如上圖中2和6兩個(gè)節(jié)點(diǎn)之間沒(méi)有邊直接連接，那么剩余其他節(jié)點(diǎn)為1，3，4，5，7，給定這些節(jié)點(diǎn)的情況下，節(jié)點(diǎn)2和節(jié)點(diǎn)6條件獨(dú)立。

綜上可知，這三種馬爾可夫性相互之間是關(guān)聯(lián)等價(jià)的，通過(guò)全局馬爾可夫性可以得到局部馬爾可夫性，通過(guò)局部馬爾可夫性也可得到成對(duì)馬爾可夫性，通過(guò)成對(duì)馬爾科夫性又可以推出全局馬爾可夫性。因此只要滿足三種性質(zhì)的一種的無(wú)向圖就稱為馬爾可夫隨機(jī)場(chǎng)(MRF)。

2.條件隨機(jī)場(chǎng)——CRF

通過(guò)上述闡述，讀者們可以對(duì)馬爾可夫隨機(jī)場(chǎng)，即馬爾可夫無(wú)向圖有了基本的掌握與理解。在此基礎(chǔ)上，本文就引出條件隨機(jī)場(chǎng)CRF。

2.1.CRF

由上述可知，CRF模型是無(wú)向圖模型的一種，但是其與馬爾可夫隨機(jī)場(chǎng)(MRF)有所不同，主要區(qū)別在于MRF模型是生成模型，而CRF模型是判別式模型，其是對(duì)條件分布進(jìn)行建模。兩者之間也存在關(guān)聯(lián)，即CRF是有條件的馬爾可夫隨機(jī)場(chǎng)，也就是在給定隨機(jī)變量的條件下的馬爾可夫隨機(jī)場(chǎng)。

CRF的基本定義為：設(shè)X和Y是隨機(jī)變量， 是給定X條件下Y的條件概率分布。若隨機(jī)變量Y構(gòu)成一個(gè)無(wú)向圖的馬爾可夫隨機(jī)場(chǎng)，則稱條件概率分布 為CRF。對(duì)應(yīng)于馬爾可夫性可理解為，如果隨機(jī)變量Y構(gòu)成一個(gè)無(wú)向圖，且圖中每一個(gè)變量Y,都滿足馬爾可夫性(至少滿足全局馬爾可夫性、局部馬爾可夫性、成對(duì)馬爾可夫性中一種)，則稱 為CRF。其中X為輸入變量，即需要標(biāo)注的觀測(cè)序列，Y為輸出變量，表示狀態(tài)或標(biāo)記序列。在自然語(yǔ)言處理領(lǐng)域中，普遍的輸入變量X和輸出變量Y具有相同圖結(jié)構(gòu)。

2.2.CRF線性鏈

在實(shí)際應(yīng)用中，對(duì)于CRF的使用最多的情況是線性鏈CRF，線性鏈的結(jié)構(gòu)如下所示：

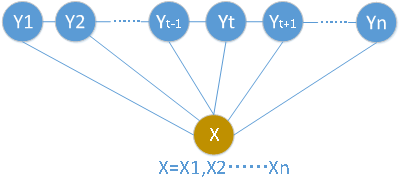
一般地，當(dāng)X和Y具有相同圖結(jié)構(gòu)時(shí)，線性鏈結(jié)構(gòu)就變?yōu)槿缦滤荆?/p>

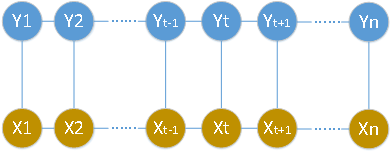
在上圖中，X就為觀測(cè)序列，Y就為狀態(tài)序列。同時(shí)在給定隨機(jī)變量序列X的條件下，如果隨機(jī)變量序列Y相對(duì)于序列X的條件概率分布P(YIX)構(gòu)成條件隨機(jī)場(chǎng)，那么可得隨機(jī)變量Y也滿足馬爾可夫性。公式表達(dá)為：

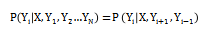
即Y當(dāng)前狀態(tài)只與相連接的前后兩個(gè)狀態(tài)有關(guān)，而與其他狀態(tài)相互獨(dú)立，為線性連接的關(guān)系。此時(shí)稱P(YIX)為條件隨機(jī)場(chǎng)，相應(yīng)的，X為輸入或者觀測(cè)序列，Y為輸出或者狀態(tài)序列。

2.3. CRF相關(guān)計(jì)算

當(dāng)選定好勢(shì)函數(shù)后，這里選取指數(shù)函數(shù)，通過(guò)引入特征函數(shù)，可以得到條件概率為：

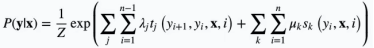
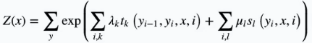
其中，t_k和 s_k分別為特征函數(shù)，t_k定義為邊上的特征函數(shù)，也叫轉(zhuǎn)移特征，它依賴于當(dāng)前節(jié)點(diǎn)和前一個(gè)節(jié)點(diǎn); s_k定義為結(jié)點(diǎn)上的特征函數(shù)，也叫狀態(tài)特征，只依賴于當(dāng)前結(jié)點(diǎn)。一般情況下，t_k和s_k的取值為1或者0，即滿足特征條件時(shí)為1，不滿足則為0。λ_k和μ_k分別為t_k和s_k所對(duì)應(yīng)的權(quán)值。Z(x)為規(guī)范化因子，來(lái)保證P(YIX)為概率分布。

對(duì)于上述公式的理解，通過(guò)一個(gè)簡(jiǎn)單例子可以更好地去掌握。例如設(shè)輸入觀測(cè)序列X X₃為（X₁，X₂，X₃）對(duì)應(yīng)的狀態(tài)序列Y為（Y₁，Y₂，Y₃），其中Y₁，Y₂，Y₃ 的取值為1或者2。對(duì)于第一條連接邊，設(shè)特征和權(quán)值為：

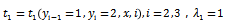
對(duì)應(yīng)的特征函數(shù)為：

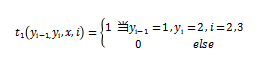
根據(jù)上式，同時(shí)給定相對(duì)應(yīng)的權(quán)重 可寫出:

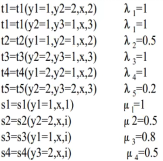
由此可計(jì)算狀態(tài)為 的非規(guī)范化條件概率為(不需要除以規(guī)范化因子Z) 。

3.CRF模型解決的三種問(wèn)題類型

相較于之前的HMM模型，CRF模型同樣需要解決三種問(wèn)題，分別為概率計(jì)算問(wèn)題、預(yù)測(cè)問(wèn)題和學(xué)習(xí)問(wèn)題。

• 概率計(jì)算問(wèn)題：針對(duì)于概率計(jì)算問(wèn)題，通常情況給定的已知信息是CRF模型的條件概率分布P(YIX)、觀測(cè)序列X和狀態(tài)序列Y，求解目標(biāo)為某一條件概率以及相對(duì)應(yīng)的數(shù)學(xué)期望。求解的方法基本就是前向后向計(jì)算方法。
• 預(yù)測(cè)問(wèn)題：針對(duì)于預(yù)測(cè)問(wèn)題，通常情況給定的已知信息是CRF模型的條件概率分布P(YIX)、觀測(cè)序列X，求解目標(biāo)為使得條件概率最大的狀態(tài)序列Y，即求解觀測(cè)序列所對(duì)應(yīng)的狀態(tài)。求解方法基本是函數(shù)計(jì)算。
• 學(xué)習(xí)問(wèn)題：學(xué)習(xí)問(wèn)題也叫模型訓(xùn)練求解參數(shù)問(wèn)題，通過(guò)給定的數(shù)據(jù)集(觀測(cè)序列和狀態(tài)序列等)來(lái)求解CRF模型所需要的參數(shù)，通常用到的方法就是模型訓(xùn)練常用的尺度迭代方法(如梯度下降算法等)。

4.總結(jié)

相較于HMM模型，CRF模型計(jì)算的過(guò)程更為復(fù)雜，但是對(duì)于整體把握CRF模型的影響并不大，只需要在思路上明白CRF模型和HMM模型在實(shí)際應(yīng)用中所需要解決的三種問(wèn)題即可，針對(duì)于特定問(wèn)題中給定的已知條件來(lái)實(shí)現(xiàn)求解目標(biāo)。

在自然語(yǔ)言處理領(lǐng)域，對(duì)于概率統(tǒng)計(jì)模型的掌握其實(shí)也就是對(duì)于HMM模型和CRF模型的掌握。雖然，HMM和CRF模型流行于在自然語(yǔ)言處理領(lǐng)域使用深度學(xué)習(xí)技術(shù)之前，但是還是那句話，目前針對(duì)于自然語(yǔ)言處理領(lǐng)域深度學(xué)習(xí)技術(shù)的瓶頸問(wèn)題，不妨換個(gè)思維，考慮下概率統(tǒng)計(jì)模型來(lái)處理，也許能取得不錯(cuò)的效果。

作者介紹

稀飯，51CTO社區(qū)編輯，曾任職某電商人工智能研發(fā)中心大數(shù)據(jù)技術(shù)部門，做推薦算法。目前攻讀智能網(wǎng)絡(luò)與大數(shù)據(jù)方向的研究生，主要擅長(zhǎng)領(lǐng)域有推薦算法、NLP、CV，使用代碼語(yǔ)言有Java、Python、Scala。