經逆向工程,Transformer「翻譯」成數學框架 | 25位學者撰文
Transformer 是 Google 團隊在 2017 年 6 月提出的 NLP 經典之作,由 Ashish Vaswani 等人在論文《 Attention Is All You Need 》中提出。自 Transformer 出現以來,便在 NLP、CV、語音、生物、化學等領域引起了諸多進展。
Transformer 在現實世界中的應用越來越廣泛,例如 GPT-3 、LaMDA 、Codex 等都是基于 Transformer 架構構建的。然而,隨著基于 Transformer 模型的擴展,其開放性和高容量為意想不到的甚至有害的行為創造了越來越大的空間。即使在大型模型訓練完成數年后,創建者和用戶也會經常發現以前從來沒見過的模型問題。
解決這些問題的一個途徑是機械的可解釋性(mechanistic interpretability),即對 transformers 計算過程進行逆向工程,這有點類似于程序員如何嘗試將復雜的二進制文件逆向工程為人類可讀的源代碼。
如果逆向工程可行,那么我們就會有更系統的方法來解釋當前模型的安全問題、識別問題,甚至可能預見未來尚未構建的模型安全問題。這有點類似于將 Transformer 的黑箱操作進行逆向,讓這一過程變得清晰可見。之前有研究者開發了 Distill Circuits thread 項目,曾嘗試對視覺模型進行逆向工程,但到目前為止還沒有可比的 transformer 或語言模型進行逆向工程研究。
在本文中,由 25 位研究者參與撰寫的論文,嘗試采用最原始的步驟逆向 transformer。該論文由 Chris Olah 起草,Chris Olah 任職于 Anthropic 人工智能安全和研究公司,主要從事逆向工程神經網絡研究。之后 Neel Nanda 對論文初稿進行了重大修改,Nanda 目前是 DeepMind 的一名研究工程實習生。Nelson Elhage 對論文進行了詳細的編輯以提高論文章節清晰度,Nelson Elhage 曾任職于 Stripe 科技公司。
左:Neel Nanda;右:Christopher Olah
考慮到語言模型的復雜性高和規模大等特點,該研究發現,從最簡單的模型開始逆向 transformer 最有效果。該研究旨在發現簡單算法模式、主題(motifs)或是框架,然后將其應用于更復雜、更大的模型。具體來說,他們的研究范圍僅包括只有注意力塊的兩層或更少層的 transformer 模型。這與 GPT-3 這樣的 transformer 模型形成鮮明的對比,GPT-3 層數多達 96 層。

論文地址:https://transformer-circuits.pub/2021/framework/index.html#acknowledgments
該研究發現,通過以一種新的但數學上等效的方式概念化 transformer 操作,我們能夠理解這些小模型并深入了解它們的內部運作方式。值得注意的是,研究發現特定的注意頭,本文稱之為歸納頭(induction heads),可以在這些小模型中解釋上下文學習,而且這些注意力頭只在至少有兩個注意層的模型中發展。此外,該研究還介紹了這些注意力頭對特定數據進行操作的一些示例。
各章節內容概覽
為了探索逆向工程 transformers 面臨哪些挑戰,研究者對幾個 attention-only 的 toy 模型進行了逆向功能。
首先是零層 transformers 模型的二元統計。研究者發現,二元表可以直接通過權重訪問。
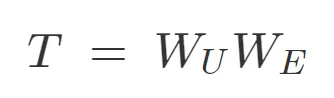
在討論更復雜的模型之前,考慮零層(zero layer)transformer 很有用。這類模型接受一個 token,嵌入,再取消嵌入,以生成預測下一個 token 的 logits
由于這類模型無法從其他 tokens 傳輸信息,因此只能從當前 token 預測下一個 token。這意味著,W_UW_E 的最優行為是近似二元對數似然。

零層 attention-only transformers 模型。
其次,單層 attention-only transformers 是二元和 skip 三元模型的集合。同零層 transformers 一樣,二元和 skip 三元表可以直接通過權重訪問,無需運行模型。這些 skip 三元模型的表達能力驚人,包括實現一種非常簡單的上下文內學習。
對于單層 attention-only transformers 模型,有哪些路徑擴展(path expansion)技巧呢?研究者提供了一些。
如下圖所示,單層 attention-only transformers 由一個 token 嵌入組成,后接一個注意力層(單獨應用注意力頭),最后是解除嵌入:

使用之前得到的張量標記(tensor notation)和注意力頭的替代表征,研究者可以將 transformer 表征為三個項的乘積,具體如下圖所示:
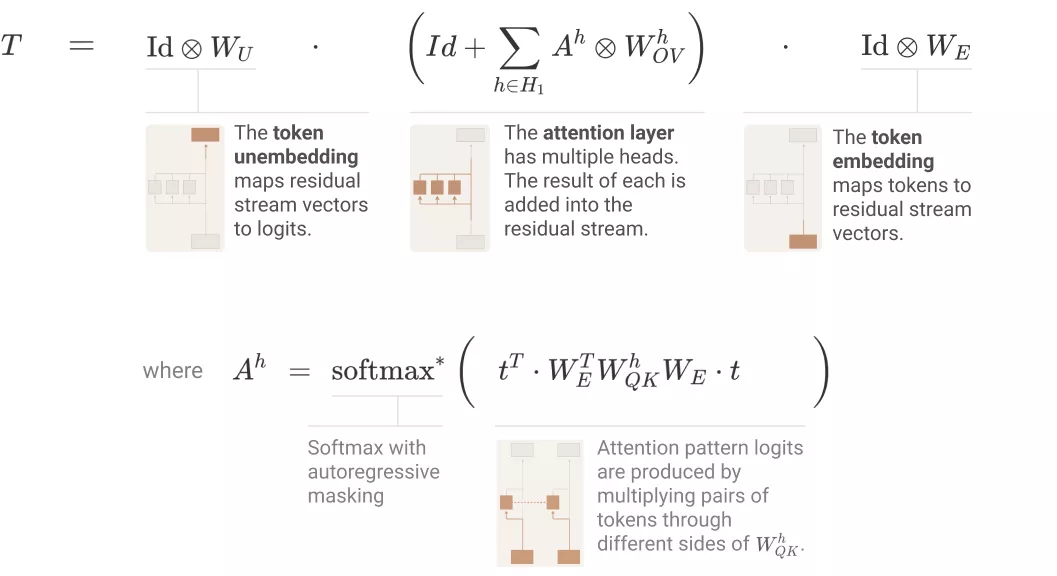
研究者采用的核心技巧是簡單地擴展乘積,即將乘積(每個項對應一個層)轉換為一個和,其中每個項對應一個端到端路徑。他們表示,每個端到端路徑項都易于理解,可以獨立地進行推理,并能夠疊加組合創建模型行為。

最后,兩層 attention-only transformers 模型可以使用注意力頭組合實現復雜得多的算法。這些組合算法也可以直接通過權重檢測出來。需要注意的是,兩層模型適應注意力頭組合創建「歸納頭」(induction heads),這是一種非常通用的上下文內學習算法。
具體地,當注意力頭有以下三種組合選擇:
- Q - 組合:W_Q 在一個受前面頭影響的子空間中讀取;
- K - 組合:W_K 在一個受前面頭影響的子空間中讀取;
- V - 組合:W_V 在一個受前面頭影響的子空間中讀取。
研究者表示,Q - 和 K - 組合與 V - 組合截然不同。前兩者都對注意力模式產生影響,允許注意力頭表達復雜得多的模式。而 V - 組合對一個注意力頭專注于某個給定位置時所要傳輸的信息產生影響。結果是,V - 組合頭變現得更像一個單一單元,并可以考慮用來創建額外的「虛擬注意力頭」。
對于 transformer 有一個最基礎的問題,即「如何計算 logits」?與單層模型使用的方法一樣,研究者寫出了一個乘積,其中每個項在模型中都是一個層,并擴展以創建一個和,其中每個項在模型中都是一個端到端路徑。
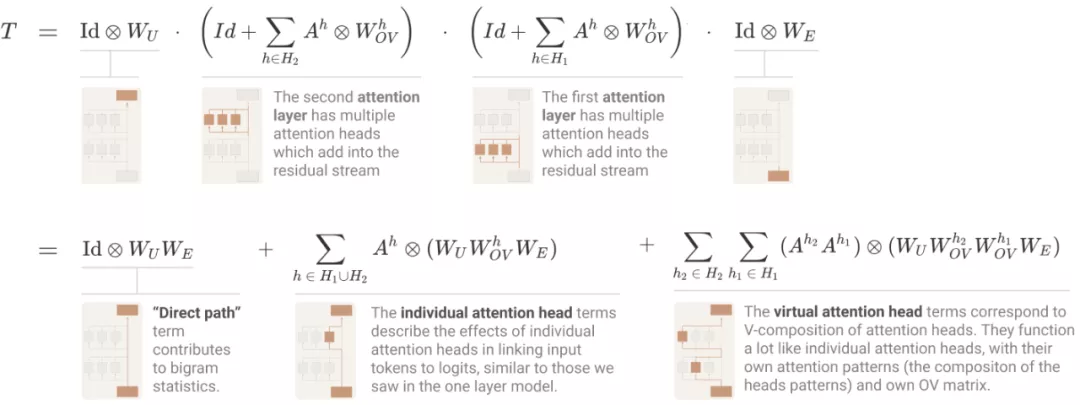
其中,直接路徑項和單個頭項與單層模型中的相同。最后的「虛擬注意力頭」項對應于 V - 組合。虛擬注意力頭在概念上非常有趣,但在實踐中,研究者發現它們往往無法在小規模的兩層模型中發揮重大作用。
此外,這些項中的每一個都對應于模型可以實現更復雜注意力模式的一種方式。在理論上,很難對它們進行推理。但當討論到歸納頭時,會很快在具體實例中用到它們。




































