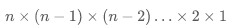[[439357]]

本文轉(zhuǎn)載自微信公眾號(hào)「程序員千羽」，作者程序員千羽。轉(zhuǎn)載本文請(qǐng)聯(lián)系程序員千羽公眾號(hào)。

 Leetcode : https://leetcode-cn.com/problems/zi-fu-chuan-de-pai-lie-lcof/

“GitHub : https://github.com/nateshao/leetcode/blob/main/algo-notes/src/main/java/com/nateshao/sword_offer/topic_30_permutation/Solution.java

字符串的排列

“題目描述 ：輸入一個(gè)字符串，打印出該字符串中字符的所有排列。你可以以任意順序返回這個(gè)字符串?dāng)?shù)組，但里面不能有重復(fù)元素。為了讓您更好地理解問(wèn)題，以下面的二叉搜索樹(shù)為例：難度：中等示例:

輸入：s = "abc" 
 
輸出：["abc","acb","bac","bca","cab","cba"] 

解題思路：

對(duì)于一個(gè)長(zhǎng)度為 n 的字符串(假設(shè)字符互不重復(fù))，其排列方案數(shù)共有：

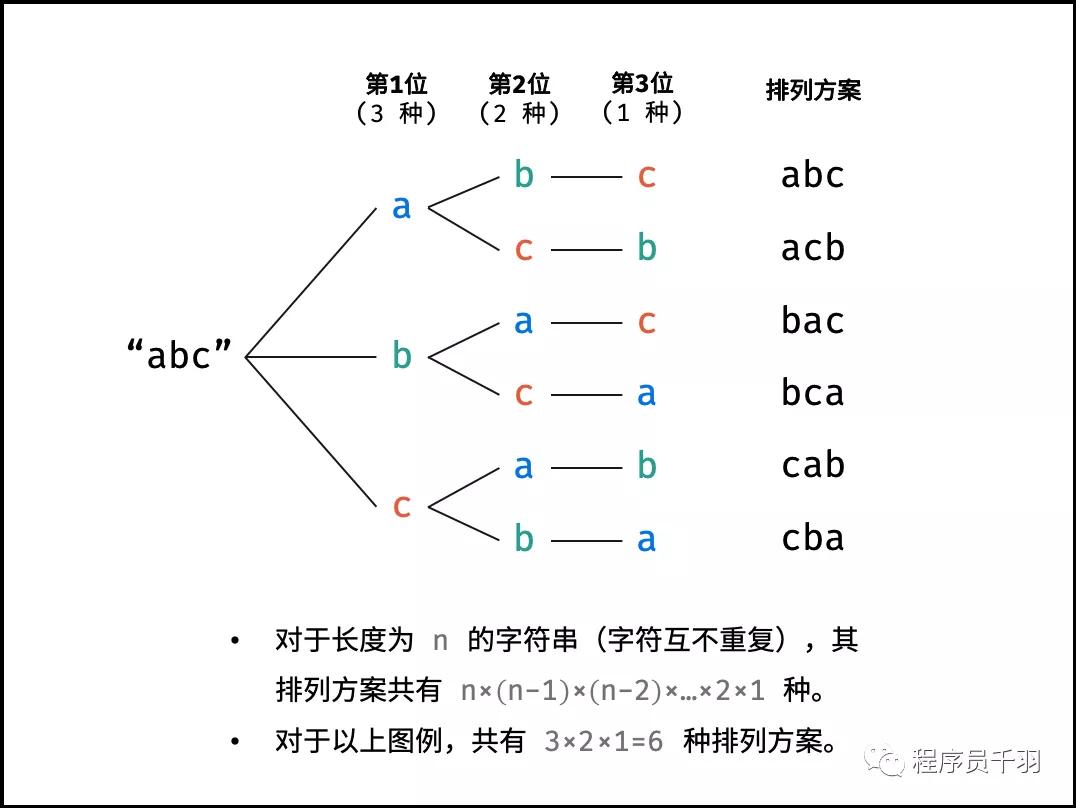
排列方案的生成：根據(jù)字符串排列的特點(diǎn)，考慮深度優(yōu)先搜索所有排列方案。即通過(guò)字符交換,先固定第1位字符( n種情況)、再固定第2位字符(n-1種情況)、...、最后固定第n位字符(1種情況)。

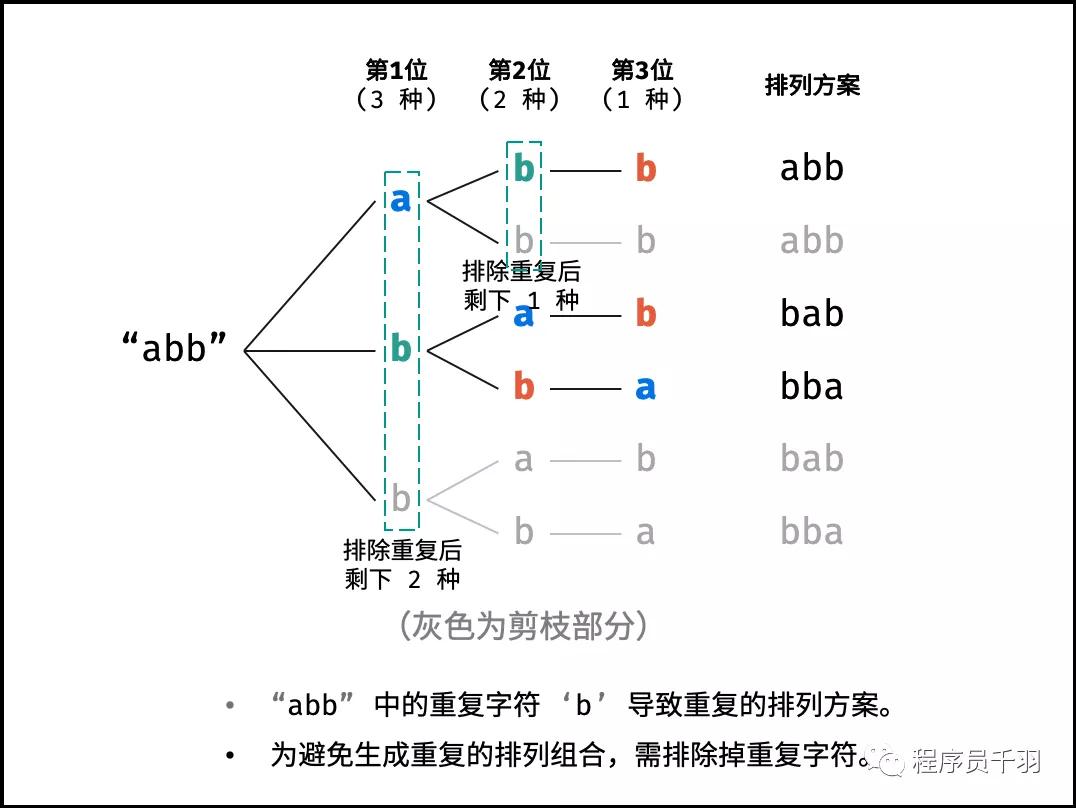
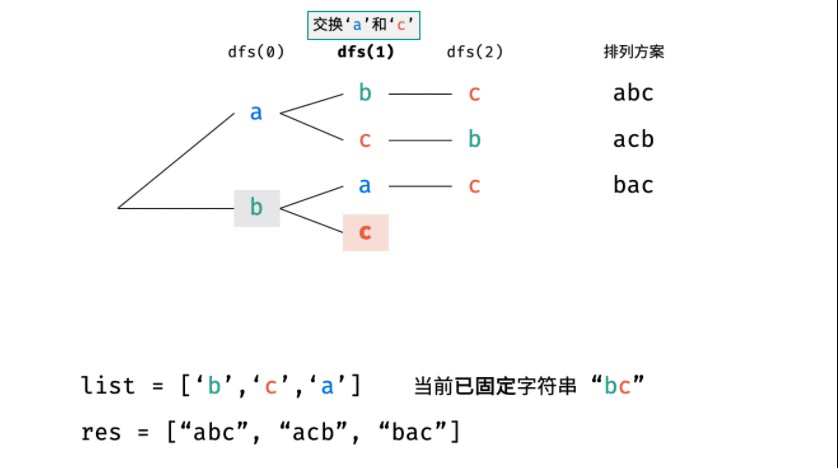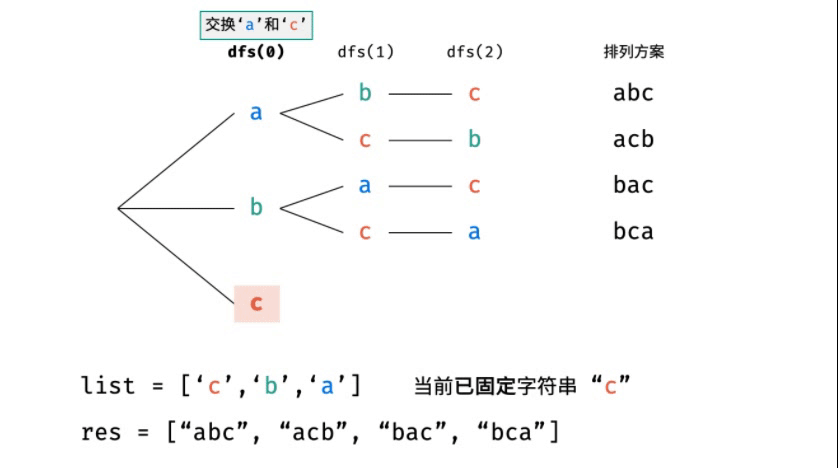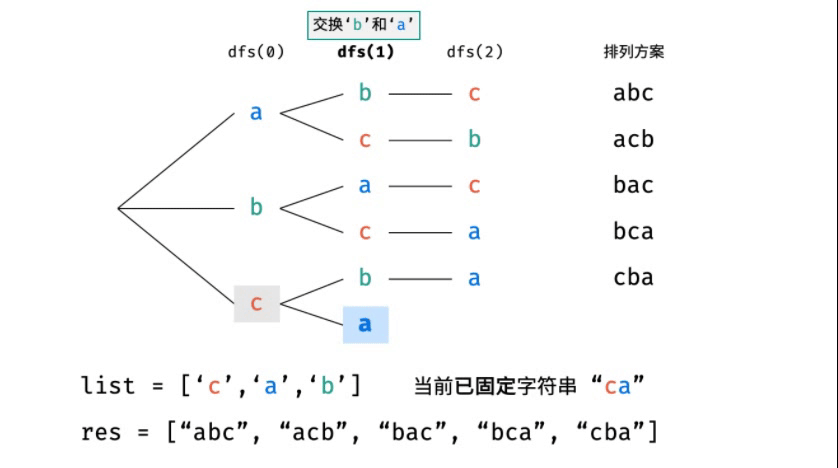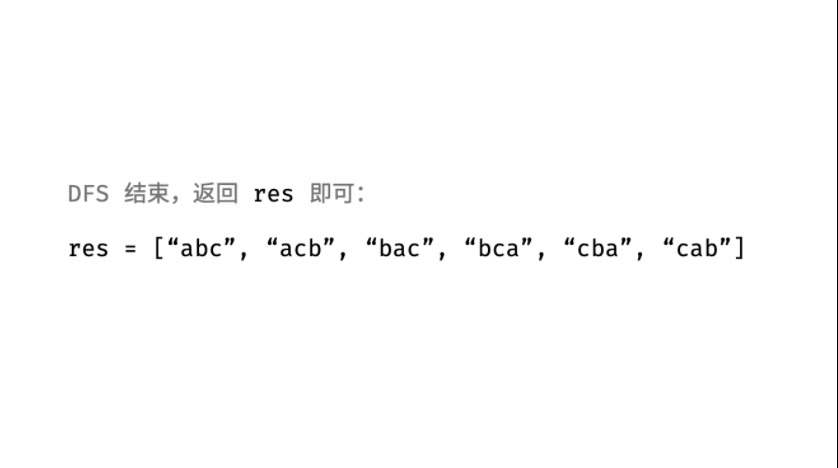
重復(fù)排列方案與剪枝：當(dāng)字符串存在重復(fù)字符時(shí)，排列方案中也存在重復(fù)的排列方案。為排除重復(fù)方案，需在固定某位字符時(shí)，保證“每種字符只在此位固定一次” ，即遇到重復(fù)字符時(shí)不交換，直接跳過(guò)。從DFS角度看，此操作稱(chēng)為"剪枝” 。

遞歸解析：

• 終止條件： 當(dāng) x = len(c) - 1 時(shí)，代表所有位已固定(最后一位只有 11 種情況)，則將當(dāng)前組合 c 轉(zhuǎn)化為字符串并加入 res ，并返回;
• 遞推參數(shù)： 當(dāng)前固定位 x ;
• 遞推工作： 初始化一個(gè) Set ，用于排除重復(fù)的字符;將第 x 位字符與 i ∈ [x, len(c)] 字符分別交換，并進(jìn)入下層遞歸;
  • 剪枝： 若 c[i] 在 Set 中，代表其是重復(fù)字符，因此 “剪枝” ;
  • 將 c[i] 加入 Set ，以便之后遇到重復(fù)字符時(shí)剪枝;
  • 固定字符： 將字符 c[i] 和 c[x] 交換，即固定 c[i] 為當(dāng)前位字符;
  • 開(kāi)啟下層遞歸： 調(diào)用 dfs(x + 1) ，即開(kāi)始固定第 x + 1 個(gè)字符;
  • 還原交換： 將字符 c[i] 和 c[x] 交換(還原之前的交換);

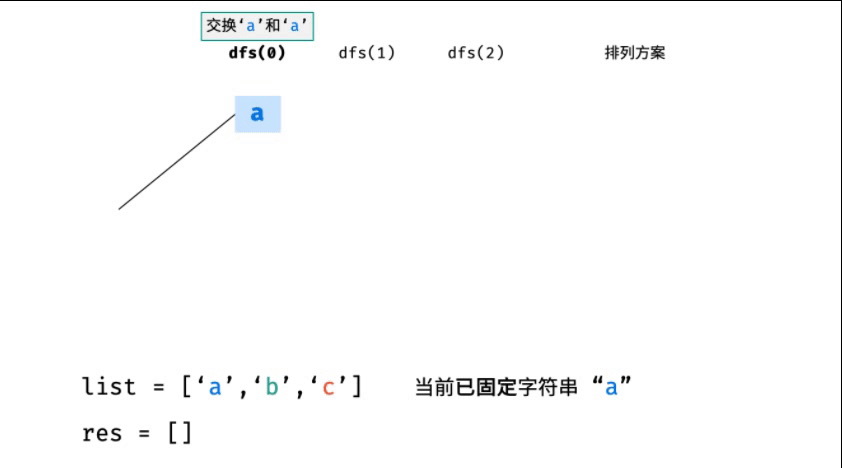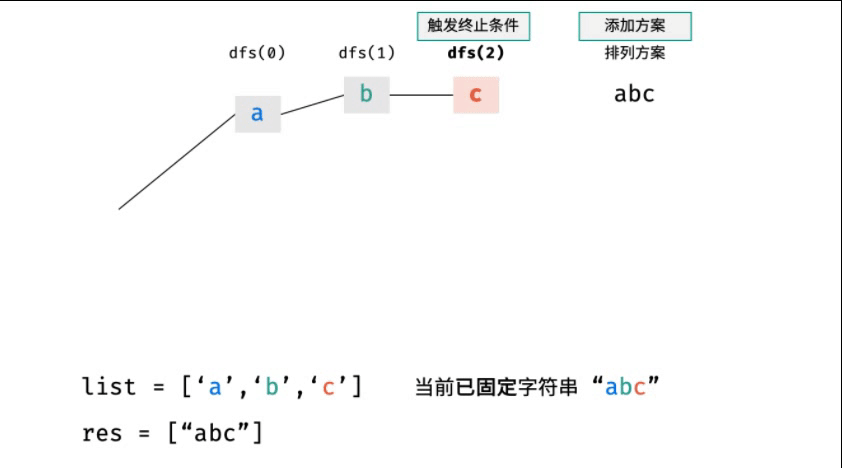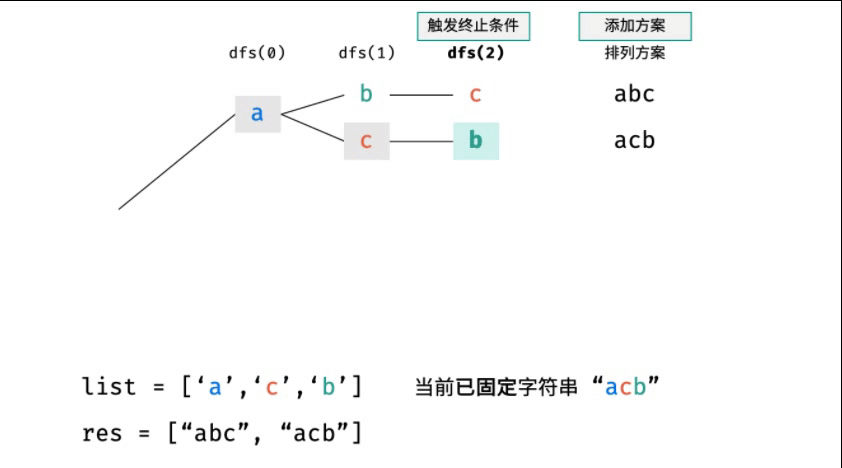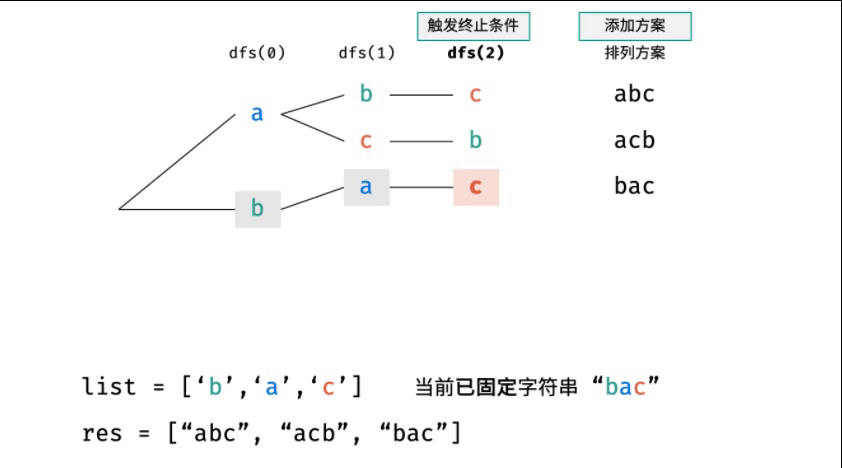
下圖中 list 對(duì)應(yīng)文中的列表 c 。比如

舉個(gè)例子：

通過(guò)交換來(lái)固定某個(gè)位置的元素這個(gè)思路， 
就 abc 這個(gè)字符串來(lái)說(shuō)，第一個(gè)位置可以放 a 或者 b 或者 c，但是如果確定要放某個(gè)字符， 
比如第一個(gè)位置放 a，那么第二個(gè)位置就只能放 b 或者 c； 
如果第一個(gè)位置放 b，那么第二個(gè)位置就只能放 a 或者 c； 
如果第一個(gè)位置放 c，那么第二個(gè)位置就只能放 a 或者 b； 
當(dāng)把某個(gè)字符移動(dòng)到第一位以后，暫時(shí)第一位的字符就固定住了， 
這時(shí)再去確定第二個(gè)位置的元素，并且此時(shí)第一個(gè)位置的元素不會(huì)再出現(xiàn)在后面的位置上， 
依次類(lèi)推直到確定所有位置的元素，再往前回溯確定每個(gè)位置上其他可能出現(xiàn)的元素。 

復(fù)雜度分析:

• 時(shí)間復(fù)雜度0(N!N) ：N為字符串s的長(zhǎng)度;時(shí)間復(fù)雜度和字符串排列的方案數(shù)成線性關(guān)系，案數(shù)為N x(N- 1)x (N- 2)...x2x1，即復(fù)雜度為0(N!) ;

字符串拼接操作join() 使用O(N)因此總體時(shí)間復(fù)雜度為O(N!N)。

• 空間復(fù)雜度0(N2) ：全排列的遞歸深度為N，系統(tǒng)累計(jì)使用棧空間大小為0(N) ;

遞歸中輔助Set累計(jì)存儲(chǔ)的字符數(shù)量最多為N +(N- 1)+...+2+1=(N + 1)N/2 ,即占用O(N2)的額外空間。

package com.nateshao.sword_offer.topic_30_permutation; 
 
import java.util.ArrayList; 
import java.util.Collections; 
import java.util.HashSet; 
import java.util.List; 
 
/** 
 * @date Created by 邵桐杰 on 2021/12/2 15:31 
 * @微信公眾號(hào) 程序員千羽 
 * @個(gè)人網(wǎng)站 www.nateshao.cn 
 * @博客 https://nateshao.gitee.io 
 * @GitHub https://github.com/nateshao 
 * @Gitee https://gitee.com/nateshao 
 * Description: 劍指 Offer 38. 字符串的排列 
 */ 
public class Solution { 
 
    public static void main(String[] args) { 
        String str = "abc"; 
        ArrayList<String> list = permutation2(str); 
        list.stream().forEach(lists-> System.out.print( lists+" " )); // abc acb bac bca cab cba 
        System.out.println(); 
        for (String s : list) { 
            System.out.print(s + " "); // abc acb bac bca cab cba 
        } 
    } 
     
    /** 
     * 劍指offer 
     * 解題思路：將當(dāng)前位置的字符和前一個(gè)字符位置交換，遞歸. 
     * @param str 
     * @return 
     */ 
    public static ArrayList<String> permutation2(String str) { 
        ArrayList<String> res = new ArrayList<>(); 
        if (str == null) return res; 
        helper(res, 0, str.toCharArray()); 
        // 符合結(jié)果的輸出順序 
        Collections.sort(res); 
        return res; 
 
    } 
 
    private static void helper(ArrayList<String> res, int index, char[] s) { 
        if (index == s.length - 1) { 
            res.add(String.valueOf(s)); 
            return; 
        } 
        for (int i = index; i < s.length; i++) { 
            if (i == index || s[index] != s[i]) { 
                swap(s, index, i); 
                helper(res, index + 1, s); 
                swap(s, index, i); 
            } 
        } 
    } 
     
    public static void swap(char[] c, int a, int b) { 
        char temp = c[a]; 
        c[a] = c[b]; 
        c[b] = temp; 
    } 
    /********************** 精選解答 **************************/ 
    //為了讓遞歸函數(shù)添加結(jié)果方便，定義到函數(shù)之外，這樣無(wú)需帶到遞歸函數(shù)的參數(shù)列表中 
    List<String> list = new ArrayList<>(); 
    //同；但是其賦值依賴(lài)c，定義聲明分開(kāi) 
    char[] c; 
    public String[] permutation(String s) { 
        c = s.toCharArray(); 
        //從第一層開(kāi)始遞歸 
        dfs(0); 
        //將字符串?dāng)?shù)組ArrayList轉(zhuǎn)化為String類(lèi)型數(shù)組 
        return list.toArray(new String[list.size()]); 
    } 
 
    public void dfs(int x) { 
        //當(dāng)遞歸函數(shù)到達(dá)第三層，就返回，因?yàn)榇藭r(shí)第二第三個(gè)位置已經(jīng)發(fā)生了交換 
        if (x == c.length - 1) { 
            //將字符數(shù)組轉(zhuǎn)換為字符串 
            list.add(String.valueOf(c)); 
            return; 
        } 
        //為了防止同一層遞歸出現(xiàn)重復(fù)元素 
        HashSet<Character> set = new HashSet<>(); 
        //這里就很巧妙了,第一層可以是a,b,c那么就有三種情況，這里i = x,正巧dfs(0)，正好i = 0開(kāi)始 
        // 當(dāng)?shù)诙又挥袃煞N情況，dfs(1）i = 1開(kāi)始 
        for (int i = x; i < c.length; i++){ 
            //發(fā)生剪枝，當(dāng)包含這個(gè)元素的時(shí)候，直接跳過(guò) 
            if (set.contains(c[i])){ 
                continue; 
            } 
            set.add(c[i]); 
            //交換元素，這里很是巧妙，當(dāng)在第二層dfs(1),x = 1,那么i = 1或者 2， 不是交換1和1，要就是交換1和2 
            swap(i,x); 
            //進(jìn)入下一層遞歸 
            dfs(x + 1); 
            //返回時(shí)交換回來(lái)，這樣保證到達(dá)第1層的時(shí)候，一直都是abc。這里捋順一下，開(kāi)始一直都是abc，那么第一位置總共就3個(gè)交換 
            //分別是a與a交換，這個(gè)就相當(dāng)于 x = 0, i = 0; 
            //     a與b交換            x = 0, i = 1; 
            //     a與c交換            x = 0, i = 2; 
            //就相當(dāng)于上圖中開(kāi)始的三條路徑 
            //第一個(gè)元素固定后，每個(gè)引出兩條路徑, 
            //     b與b交換            x = 1, i = 1; 
            //     b與c交換            x = 1, i = 2; 
            //所以，結(jié)合上圖，在每條路徑上標(biāo)注上i的值，就會(huì)非常容易好理解了 
            swap(i,x); 
        } 
    } 
    private void swap(int i, int x) { 
        char temp = c[i]; 
        c[i] = c[x]; 
        c[x] = temp; 
    } 
} 

參考文章：https://leetcode-cn.com/problems/zi-fu-chuan-de-pai-lie-lcof/solution/mian-shi-ti-38-zi-fu-chuan-de-pai-lie-hui-su-fa-by