北大數(shù)院校友成果登數(shù)學(xué)四大頂刊,偏微分方程突破,可用于W-GAN
本文經(jīng)AI新媒體量子位(公眾號(hào)ID:QbitAI)授權(quán)轉(zhuǎn)載,轉(zhuǎn)載請(qǐng)聯(lián)系出處。
數(shù)學(xué)界神秘的偏微分方程領(lǐng)域,再次被突破了!
來(lái)自中科大的陳世炳教授等人,開(kāi)發(fā)了一套全新的數(shù)學(xué)方法,直接打破了領(lǐng)域內(nèi)專(zhuān)家20多年來(lái)的既有認(rèn)知。
相關(guān)論文已被數(shù)學(xué)四大頂刊之一《數(shù)學(xué)年刊》接受,將在接下來(lái)的某一期正式發(fā)表。

這篇論文突破了一個(gè)關(guān)鍵的非線性偏微分方程,它與我們機(jī)器學(xué)習(xí)中熟悉的最優(yōu)傳輸理論息息相關(guān)。
最優(yōu)傳輸理論,類(lèi)似“找出把物品從A運(yùn)到B的最佳方法”,用幾何方法來(lái)衡量概率分布的距離、給概率分布建模。像機(jī)器學(xué)習(xí)中的W-GAN,就屬于最優(yōu)傳輸問(wèn)題。
讓丘成桐院士1982年獲菲爾茨獎(jiǎng)的卡拉比猜想證明,就與這個(gè)方程相關(guān)。
2018年的菲爾茨獎(jiǎng),再次頒給了在這個(gè)方程、以及最優(yōu)傳輸問(wèn)題上做出貢獻(xiàn)的Alessio Figalli。
究竟是什么方程如此關(guān)鍵,這次數(shù)學(xué)家們又做出了什么重要突破?
一起來(lái)看看。
最優(yōu)傳輸“逃不開(kāi)”的方程
這個(gè)關(guān)鍵的非線性偏微分方程,名叫蒙日-安培方程。
它的提出,要從18世紀(jì)法國(guó)數(shù)學(xué)家加斯帕爾·蒙日(Gaspard Monge)對(duì)最優(yōu)傳輸問(wèn)題的研究說(shuō)起。
最初,這個(gè)理論主要用來(lái)解決不連續(xù)分布的物體運(yùn)輸問(wèn)題,類(lèi)似于搬箱子:
將ABC初始地的箱子運(yùn)到CDE目的地,確保每個(gè)目的地有1個(gè)箱子,求最佳的運(yùn)輸方法。
后來(lái),蒙日開(kāi)始思考一類(lèi)問(wèn)題:對(duì)于連續(xù)分布的物體,例如一團(tuán)沙子,用什么方法將它運(yùn)輸?shù)降润w積的洞中,才是最省力的?
他發(fā)現(xiàn),有不少這類(lèi)連續(xù)情形下的最優(yōu)傳輸問(wèn)題,都能轉(zhuǎn)化為一類(lèi)方程的邊值問(wèn)題。
蒙日之后,安培進(jìn)一步對(duì)它做了深入研究,方程也被命名為蒙日-安培方程:
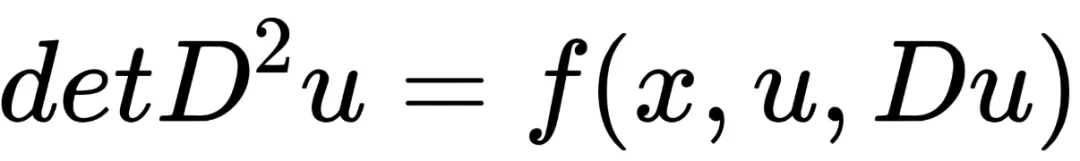
△蒙日-安培方程一般形式
這個(gè)方程要怎么理解呢?
舉個(gè)例子,我們常見(jiàn)的“以圖搜圖”功能,其實(shí)就與蒙日-安培方程相關(guān)。
在通過(guò)圖像匹配進(jìn)行搜索時(shí),“搜圖”功能會(huì)將輸入圖像與網(wǎng)上的圖像進(jìn)行一個(gè)對(duì)比。以黑白照片為例,可以將顏色深度看成是一個(gè)概率分布(白色為0,黑色為1)。
因此,兩張照片匹配的問(wèn)題,可以看成是兩個(gè)概率分布的匹配問(wèn)題。
1991年,Yann Brenier在研究中發(fā)現(xiàn),這類(lèi)連續(xù)概率分布的匹配問(wèn)題,對(duì)應(yīng)地可以寫(xiě)成一個(gè)梯度映射y=Du(x), 其中u是一個(gè)凸函數(shù), 且滿足
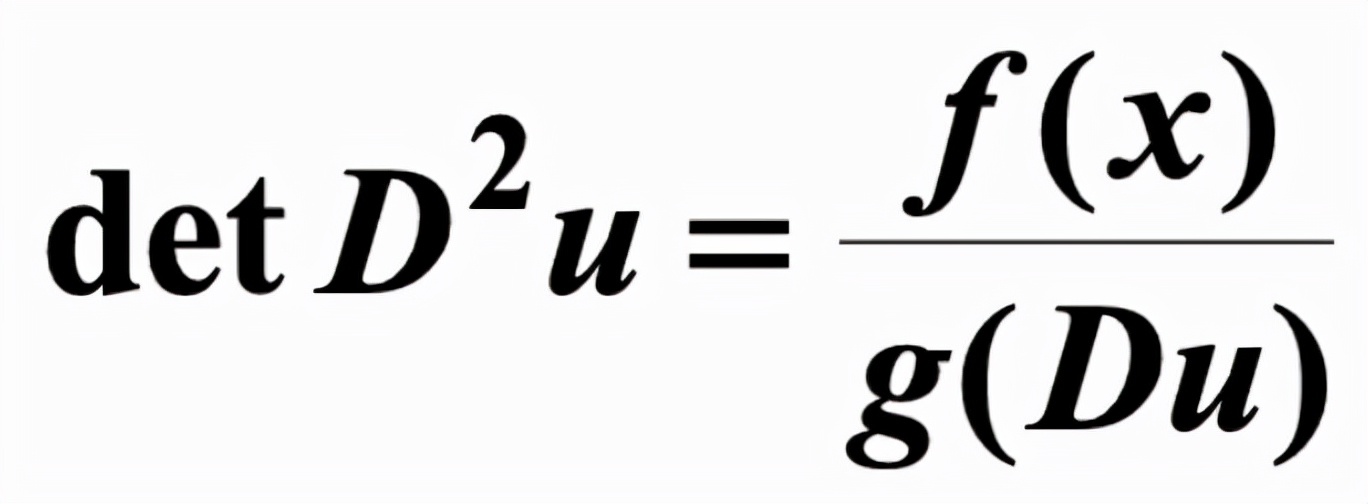
根據(jù)黑塞矩陣(Hessian Matrix),有:
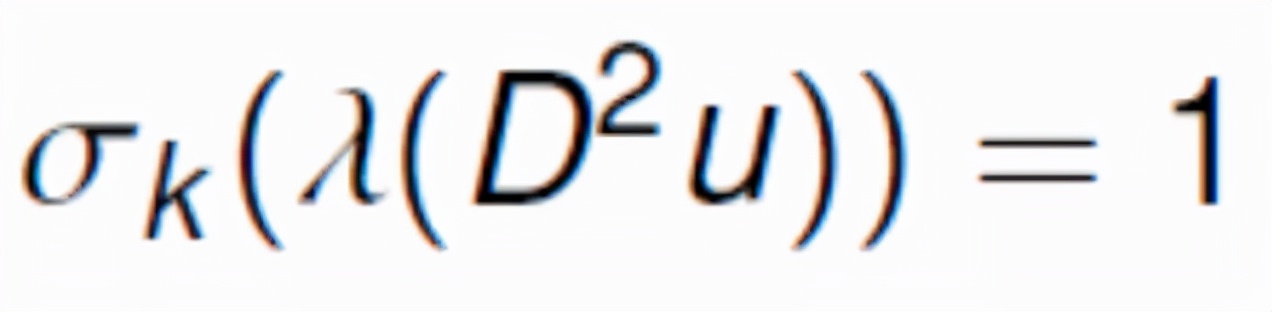
其中λ是u的黑塞矩陣的特征根,是λ的k次初等多項(xiàng)式:
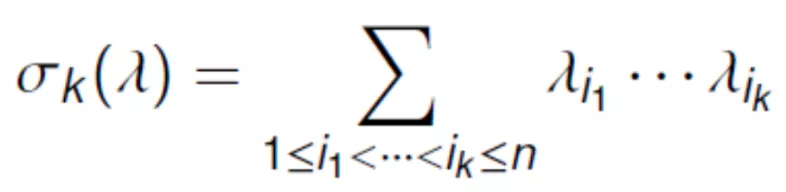
當(dāng)k=1時(shí),它就是我們熟悉的Laplace方程;當(dāng)k=n時(shí),它就是蒙日-安培方程。
近幾年,深度學(xué)習(xí)飛速發(fā)展,最優(yōu)傳輸問(wèn)題隨之成為研究熱點(diǎn),對(duì)蒙日-安培方程的研究也進(jìn)一步興起。
名噪一時(shí)的Wasserstein GAN,用求Wasserstein距離的方法改善了GAN的穩(wěn)定性。
求解Wasserstein距離正是一個(gè)最優(yōu)傳輸問(wèn)題,需要用到蒙日-安培方程。
紐約州立大學(xué)石溪分校的顧險(xiǎn)峰教授認(rèn)為,深度學(xué)習(xí)用到的數(shù)據(jù)可以看成是高維數(shù)據(jù)空間中一個(gè)低維流形上的概率分布。
GAN所學(xué)習(xí)的正是這個(gè)流形的結(jié)構(gòu),用編碼、解碼映射來(lái)表示,就將GAN隱空間中的數(shù)據(jù)分布轉(zhuǎn)換成了幾何上的最優(yōu)傳輸問(wèn)題。
據(jù)顧險(xiǎn)峰教授介紹,這幾年隨著醫(yī)學(xué)圖像技術(shù)、無(wú)線通訊技術(shù)、3D 打印技術(shù)、VR/AR技術(shù)的發(fā)展,以蒙日-安培方程為代表的非線性偏微分方程理論,開(kāi)始廣泛用于CS和其他工程領(lǐng)域。
那么,這次陳世炳教授等人發(fā)表在《數(shù)學(xué)年刊》上的研究,究竟做出了什么突破?
打破二十多年的“定論”
研究一個(gè)方程的重要思路,就是研究解的性質(zhì)。
蒙日-安培方程理論也不例外,它主要研究解的存在性、唯一性和光滑性(正則性)。
光滑性(正則性)通常用來(lái)描述函數(shù)的光滑程度。如果一個(gè)函數(shù)是光滑的,這個(gè)函數(shù)在數(shù)學(xué)定義上無(wú)窮可導(dǎo)。
其中,存在性證明已經(jīng)由Alexandrov給出,而弱解(某種精確定義的意義下滿足該方程的解)的唯一性也已經(jīng)得到證明。
對(duì)光滑性的研究,自1996年來(lái)卻一直局限在某些條件下。
1996年,Caffarelli在他里程碑式的工作中,證明了當(dāng)兩個(gè)區(qū)域是一致凸、密度函數(shù)光滑的時(shí)候,最優(yōu)傳輸解光滑。
然而這里有一些限制條件:兩個(gè)區(qū)域一致凸、密度函數(shù)光滑。
二十多年來(lái),領(lǐng)域里的專(zhuān)家?guī)缀醵颊J(rèn)為這些條件(尤其是區(qū)域一致凸)必不可少。
但陳世炳等人在這次的研究中,去掉了兩區(qū)域一致凸條件,甚至降低了對(duì)邊界的光滑性要求,證明了自然邊界條件下蒙日-安培方程的整體光滑性。
這對(duì)于蒙日-安培方程的研究來(lái)說(shuō),是一大進(jìn)步,相當(dāng)于把一個(gè)定理的范圍擴(kuò)大到了更廣泛的領(lǐng)域。
作者介紹
作者陳世炳,現(xiàn)在任中國(guó)科學(xué)技術(shù)大學(xué)數(shù)學(xué)系特任教授,博士生導(dǎo)師。
據(jù)鎮(zhèn)海中學(xué)梓蔭山下微博賬號(hào)消息,陳世炳是寧波鎮(zhèn)海中學(xué)2001屆校友。
鎮(zhèn)海中學(xué)是浙江省強(qiáng)校,除了陳世炳,還有包括IOI金牌得主羅煜翔等人也出自這里。
陳世炳本碩畢業(yè)于北京大學(xué)數(shù)學(xué)系,博士畢業(yè)于加拿大多倫多大學(xué)。
曾先后在美國(guó)國(guó)家數(shù)學(xué)科學(xué)研究所和澳洲國(guó)立大學(xué)任博士后,與菲爾茨獎(jiǎng)得主Alessio Figalli以及澳大利亞科學(xué)院院士汪徐家教授有長(zhǎng)期合作。
他的主要研究領(lǐng)域?yàn)榉蔷€性偏微分方程,除了蒙日-安培方程之外也在曲率流、不等式以及 Lp Minkowski問(wèn)題方面取得了若干成果,目前已發(fā)表SCI論文十余篇。
作者劉佳堃,澳大利亞伍倫貢大學(xué)數(shù)學(xué)與應(yīng)用統(tǒng)計(jì)學(xué)院教授,本科畢業(yè)于浙江大學(xué),曾獲陳省身數(shù)學(xué)獎(jiǎng)學(xué)金。
作者汪徐家,澳大利亞科學(xué)院院士,曾獲華人數(shù)學(xué)最高獎(jiǎng)“晨興數(shù)學(xué)獎(jiǎng)”金獎(jiǎng),同樣在蒙日-安培方程上有深入研究,尤其是其中的正則性理論。
據(jù)顧險(xiǎn)峰教授介紹,他與合作者給出了Ma-Trudinger-Wang條件,來(lái)限定密度函數(shù),傳輸代價(jià)和概率測(cè)度支集的幾何性質(zhì),從而保證最優(yōu)傳輸映射的光滑性。
同時(shí),他還厘清了反射曲面設(shè)計(jì)、自由曲面透鏡設(shè)計(jì)等價(jià)于球面上的最優(yōu)傳輸問(wèn)題,也等價(jià)于球面上的蒙日-安培方程。
國(guó)內(nèi)學(xué)者在這一方程上的突破歷程,可以說(shuō)是非常精彩了。
論文地址:
https://arxiv.org/pdf/1802.07518.pdf
顧險(xiǎn)峰教授談蒙日-安培方程(授權(quán)引用):
https://mp.weixin.qq.com/s/qf_lL4Wl5P9nAKv2fGklRQ