聽說遞歸能做的，棧也能做！

作者：程序員Carl 2021-07-15 11:31:22

我們在棧與隊(duì)列：匹配問題都是棧的強(qiáng)項(xiàng)中提到了，遞歸的實(shí)現(xiàn)就是：每一次遞歸調(diào)用都會(huì)把函數(shù)的局部變量、參數(shù)值和返回地址等壓入調(diào)用棧中，然后遞歸返回的時(shí)候，從棧頂彈出上一次遞歸的各項(xiàng)參數(shù)，所以這就是遞歸為什么可以返回上一層位置的原因。

[[411457]]

本文轉(zhuǎn)載自微信公眾號(hào)「代碼隨想錄」，作者程序員Carl 。轉(zhuǎn)載本文請聯(lián)系代碼隨想錄公眾號(hào)。

二叉樹的迭代遍歷

看完本篇大家可以使用迭代法，再重新解決如下三道leetcode上的題目：

144.二叉樹的前序遍歷
94.二叉樹的中序遍歷
145.二叉樹的后序遍歷

為什么可以用迭代法(非遞歸的方式)來實(shí)現(xiàn)二叉樹的前后中序遍歷呢?

此時(shí)大家應(yīng)該知道我們用棧也可以是實(shí)現(xiàn)二叉樹的前后中序遍歷了。

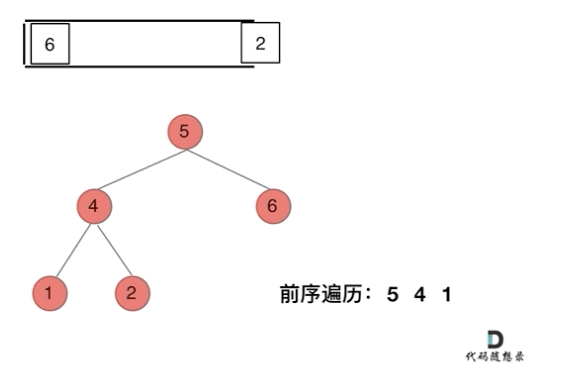
前序遍歷(迭代法)

我們先看一下前序遍歷。

前序遍歷是中左右，每次先處理的是中間節(jié)點(diǎn)，那么先將跟節(jié)點(diǎn)放入棧中，然后將右孩子加入棧，再加入左孩子。

為什么要先加入右孩子，再加入左孩子呢?因?yàn)檫@樣出棧的時(shí)候才是中左右的順序。

動(dòng)畫如下：

不難寫出如下代碼: (注意代碼中空節(jié)點(diǎn)不入棧)

class Solution { 
public: 
    vector<int> preorderTraversal(TreeNode* root) { 
        stack<TreeNode*> st; 
        vector<int> result; 
        if (root == NULL) return result; 
        st.push(root); 
        while (!st.empty()) { 
            TreeNode* node = st.top();                       // 中 
            st.pop(); 
            result.push_back(node->val); 
            if (node->right) st.push(node->right);           // 右（空節(jié)點(diǎn)不入棧） 
            if (node->left) st.push(node->left);             // 左（空節(jié)點(diǎn)不入棧） 
        } 
        return result; 
    } 
};

此時(shí)會(huì)發(fā)現(xiàn)貌似使用迭代法寫出前序遍歷并不難，確實(shí)不難。

此時(shí)是不是想改一點(diǎn)前序遍歷代碼順序就把中序遍歷搞出來了?

其實(shí)還真不行!

但接下來，再用迭代法寫中序遍歷的時(shí)候，會(huì)發(fā)現(xiàn)套路又不一樣了，目前的前序遍歷的邏輯無法直接應(yīng)用到中序遍歷上。

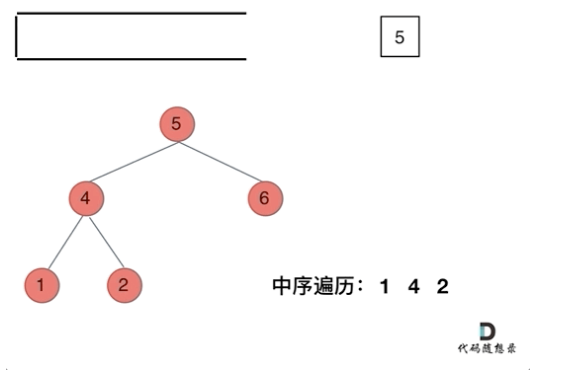
中序遍歷(迭代法)

為了解釋清楚，我說明一下剛剛在迭代的過程中，其實(shí)我們有兩個(gè)操作：

處理：將元素放進(jìn)result數(shù)組中

訪問：遍歷節(jié)點(diǎn)

分析一下為什么剛剛寫的前序遍歷的代碼，不能和中序遍歷通用呢，因?yàn)榍靶虮闅v的順序是中左右，先訪問的元素是中間節(jié)點(diǎn)，要處理的元素也是中間節(jié)點(diǎn)，所以剛剛才能寫出相對(duì)簡潔的代碼，因?yàn)橐L問的元素和要處理的元素順序是一致的，都是中間節(jié)點(diǎn)。

那么再看看中序遍歷，中序遍歷是左中右，先訪問的是二叉樹頂部的節(jié)點(diǎn)，然后一層一層向下訪問，直到到達(dá)樹左面的最底部，再開始處理節(jié)點(diǎn)(也就是在把節(jié)點(diǎn)的數(shù)值放進(jìn)result數(shù)組中)，這就造成了處理順序和訪問順序是不一致的。

那么在使用迭代法寫中序遍歷，就需要借用指針的遍歷來幫助訪問節(jié)點(diǎn)，棧則用來處理節(jié)點(diǎn)上的元素。

動(dòng)畫如下：

中序遍歷，可以寫出如下代碼：

class Solution { 
public: 
    vector<int> inorderTraversal(TreeNode* root) { 
        vector<int> result; 
        stack<TreeNode*> st; 
        TreeNode* cur = root; 
        while (cur != NULL || !st.empty()) { 
            if (cur != NULL) { // 指針來訪問節(jié)點(diǎn)，訪問到最底層 
                st.push(cur); // 將訪問的節(jié)點(diǎn)放進(jìn)棧 
                cur = cur->left;                // 左 
            } else { 
                cur = st.top(); // 從棧里彈出的數(shù)據(jù)，就是要處理的數(shù)據(jù)（放進(jìn)result數(shù)組里的數(shù)據(jù)） 
                st.pop(); 
                result.push_back(cur->val);     // 中 
                cur = cur->right;               // 右 
            } 
        } 
        return result; 
    } 
};

后序遍歷(迭代法)

再來看后序遍歷，先序遍歷是中左右，后續(xù)遍歷是左右中，那么我們只需要調(diào)整一下先序遍歷的代碼順序，就變成中右左的遍歷順序，然后在反轉(zhuǎn)result數(shù)組，輸出的結(jié)果順序就是左右中了，如下圖：

所以后序遍歷只需要前序遍歷的代碼稍作修改就可以了，代碼如下：

class Solution { 
public: 
    vector<int> postorderTraversal(TreeNode* root) { 
        stack<TreeNode*> st; 
        vector<int> result; 
        if (root == NULL) return result; 
        st.push(root); 
        while (!st.empty()) { 
            TreeNode* node = st.top(); 
            st.pop(); 
            result.push_back(node->val); 
            if (node->left) st.push(node->left); // 相對(duì)于前序遍歷，這更改一下入棧順序 （空節(jié)點(diǎn)不入棧） 
            if (node->right) st.push(node->right); // 空節(jié)點(diǎn)不入棧 
        } 
        reverse(result.begin(), result.end()); // 將結(jié)果反轉(zhuǎn)之后就是左右中的順序了 
        return result; 
    } 
};

總結(jié)

此時(shí)我們用迭代法寫出了二叉樹的前后中序遍歷，大家可以看出前序和中序是完全兩種代碼風(fēng)格，并不想遞歸寫法那樣代碼稍做調(diào)整，就可以實(shí)現(xiàn)前后中序。

這是因?yàn)榍靶虮闅v中訪問節(jié)點(diǎn)(遍歷節(jié)點(diǎn))和處理節(jié)點(diǎn)(將元素放進(jìn)result數(shù)組中)可以同步處理，但是中序就無法做到同步!

上面這句話，可能一些同學(xué)不太理解，建議自己親手用迭代法，先寫出來前序，再試試能不能寫出中序，就能理解了。

那么問題又來了，難道二叉樹前后中序遍歷的迭代法實(shí)現(xiàn)，就不能風(fēng)格統(tǒng)一么(即前序遍歷改變代碼順序就可以實(shí)現(xiàn)中序和后序)?

當(dāng)然可以，這種寫法，還不是很好理解，我們將在下一篇文章里重點(diǎn)講解，敬請期待!

其他語言版本

Java：

// 前序遍歷順序：中-左-右，入棧順序：中-右-左 
class Solution { 
    public List<Integer> preorderTraversal(TreeNode root) { 
        List<Integer> result = new ArrayList<>(); 
        if (root == null){ 
            return result; 
        } 
        Stack<TreeNode> stack = new Stack<>(); 
        stack.push(root); 
        while (!stack.isEmpty()){ 
            TreeNode node = stack.pop(); 
            result.add(node.val); 
            if (node.right != null){ 
                stack.push(node.right); 
            } 
            if (node.left != null){ 
                stack.push(node.left); 
            } 
        } 
        return result; 
    } 
} 
 
// 中序遍歷順序: 左-中-右 入棧順序： 左-右 
class Solution { 
    public List<Integer> inorderTraversal(TreeNode root) { 
        List<Integer> result = new ArrayList<>(); 
        if (root == null){ 
            return result; 
        } 
        Stack<TreeNode> stack = new Stack<>(); 
        TreeNode cur = root; 
        while (cur != null || !stack.isEmpty()){ 
           if (cur != null){ 
               stack.push(cur); 
               cur = cur.left; 
           }else{ 
               cur = stack.pop(); 
               result.add(cur.val); 
               cur = cur.right; 
           } 
        } 
        return result; 
    } 
} 
 
// 后序遍歷順序 左-右-中 入棧順序：中-左-右 出棧順序：中-右-左， 最后翻轉(zhuǎn)結(jié)果 
class Solution { 
    public List<Integer> postorderTraversal(TreeNode root) { 
        List<Integer> result = new ArrayList<>(); 
        if (root == null){ 
            return result; 
        } 
        Stack<TreeNode> stack = new Stack<>(); 
        stack.push(root); 
        while (!stack.isEmpty()){ 
            TreeNode node = stack.pop(); 
            result.add(node.val); 
            if (node.left != null){ 
                stack.push(node.left); 
            } 
            if (node.right != null){ 
                stack.push(node.right); 
            } 
        } 
        Collections.reverse(result); 
        return result; 
    } 
}

Python：

# 前序遍歷-迭代-LC144_二叉樹的前序遍歷 
class Solution: 
    def preorderTraversal(self, root: TreeNode) -> List[int]: 
        # 根結(jié)點(diǎn)為空則返回空列表 
        if not root: 
            return [] 
        stack = [root] 
        result = [] 
        while stack: 
            node = stack.pop() 
            # 中結(jié)點(diǎn)先處理 
            result.append(node.val) 
            # 右孩子先入棧 
            if node.right: 
                stack.append(node.right) 
            # 左孩子后入棧 
            if node.left: 
                stack.append(node.left) 
        return result 
         
# 中序遍歷-迭代-LC94_二叉樹的中序遍歷 
class Solution: 
    def inorderTraversal(self, root: TreeNode) -> List[int]: 
        if not root: 
            return [] 
        stack = []  # 不能提前將root結(jié)點(diǎn)加入stack中 
        result = [] 
        cur = root 
        while cur or stack: 
            # 先迭代訪問最底層的左子樹結(jié)點(diǎn) 
            if cur:      
                stack.append(cur) 
                cur = cur.left   
            # 到達(dá)最左結(jié)點(diǎn)后處理?xiàng)ｍ斀Y(jié)點(diǎn)     
            else:   
                cur = stack.pop() 
                result.append(cur.val) 
                # 取棧頂元素右結(jié)點(diǎn) 
                cur = cur.right  
        return result 
         
# 后序遍歷-迭代-LC145_二叉樹的后序遍歷 
class Solution: 
    def postorderTraversal(self, root: TreeNode) -> List[int]: 
        if not root: 
            return [] 
        stack = [root] 
        result = [] 
        while stack: 
            node = stack.pop() 
            # 中結(jié)點(diǎn)先處理 
            result.append(node.val) 
            # 左孩子先入棧 
            if node.left: 
                stack.append(node.left) 
            # 右孩子后入棧 
            if node.right: 
                stack.append(node.right) 
        # 將最終的數(shù)組翻轉(zhuǎn) 
        return result[::-1]