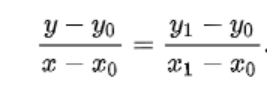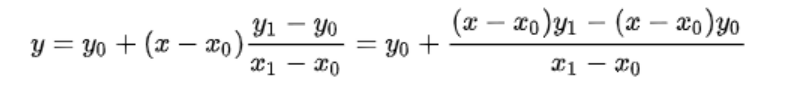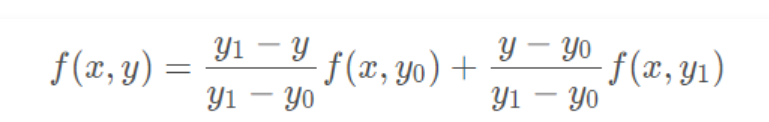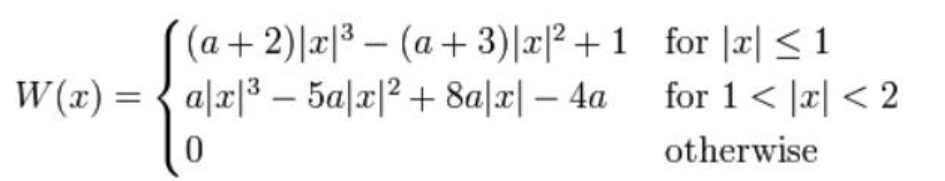[[411126]]

本文轉載自微信公眾號「Python中文社區」，作者wedo實驗君。轉載本文請聯系Python中文社區公眾號。

 1. 什么是插值

最近在做時間序列預測時，在突增或者突降的變化劇烈的情況下，擬合參數的效果不好，有用到插值的算法補全一些數據來平滑劇烈變化過程。還有在圖像處理中，也經常有用到插值算法來改變圖像的大小，在圖像超分(Image Super-Resolution)中上采樣也有插值的身影。

插值(interpolation)，顧名思義就是插入一些新的數據，當然這些值是根據已有數據生成。插值算法有很多經典算法， 本文分享如下：

• 線性插值
• 雙線性插值
• 雙三次插值bicubic interpolation

2. 插值算法原理和實現

2.1 線性插值

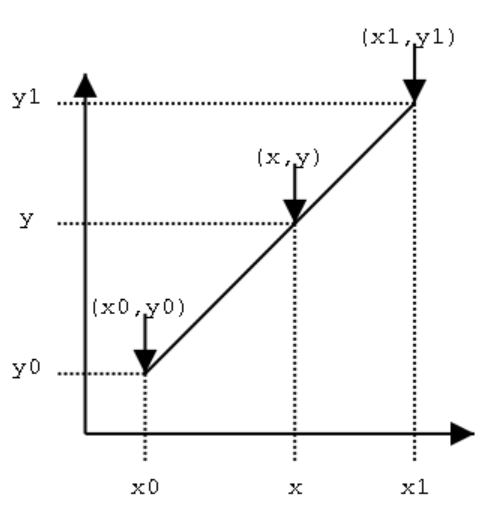
線性插值是最簡單的插值算法。如下圖已知(x0, y0) (x1, y1)，在x處插值一點(x, y)。

可以通過簡單幾何知識來推出公式

實現上直接套公式，如果想插值多個點，可以利用線性回歸的方式。

import os 
import numpy as np 
from sklearn.linear_model import LinearRegression 
def linear_interpolation(data, inter_num=4): 
    clf = LinearRegression() 
    X = np.array([[1], [inter_num+2]]) 
    y = data 
    clf.fit(X, y) 
    inter_values = clf.predict(np.array([ [i+2] for i in range(inter_num)])) 
    return inter_values 
data = [[10], [20]] 
linear_interpolation(data, 1) 
# array([[15.]]) 
def manual_linear_interpolation(x0, y0, x1, y1, x): 
    return y0+(x-x0)*(y1-y0)/(x1-x0) 
manual_linear_interpolation(1, 10, 3, 20, 2) 
# 15.0 

線性插值算法經常用在平滑數據上，也用在缺失值預處理中。

2.2 雙線性插值

雙線性插值是在兩個方向上同時進行線性插值，經常用在圖像處理中。雙線性插值是已知2*2個點，插值生成一個點的過程。

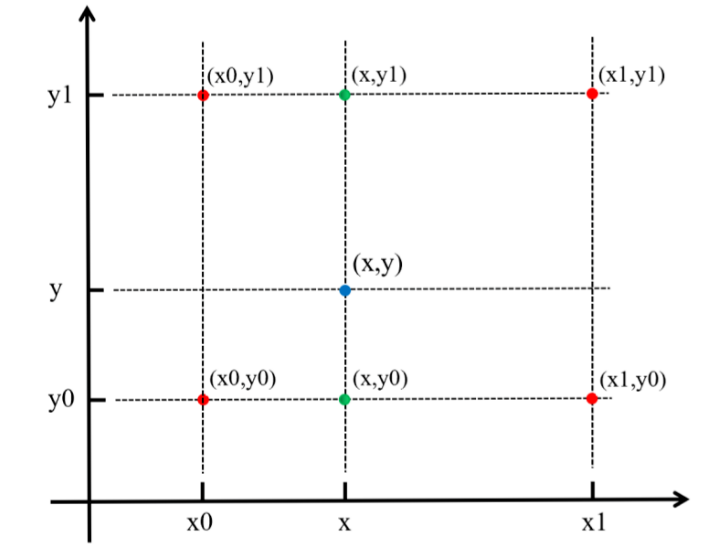
如下圖所示，雙線性插值已知(x0, y1)(x0, y0)(x1, y1)(x1, y0)4個點，插值計算(x, y)。

• 先插值生成(x, y1)(x, y0)

• 在插值生成(x, y)

import cv2 
lean_img = cv2.imread('./lena.jpg') 
lena_x2 = cv2.resize(lean_img, (0, 0), fx=2, fy=2, interpolation=cv2.INTER_LINEAR) 

2.3 雙三次插值

雙線性插值利用22個點插值生成一個新的點，而雙三次插值利用44個點來插值一個新的點。插值的過程就是如何估計aij， aij可以認為是16個點對插值點的影響因子。

影響因子設計來自于Cubic Convolution Interpolation For Digital Image Processing，

以下為Bicubic函數

import cv2 
lean_img = cv2.imread('./lena.jpg') 
lena_x2_cubic = cv2.resize(lean_img, (0, 0), fx=2, fy=2, interpolation=cv2.INTER_CUBIC) 

左邊為雙線性插值，右邊有雙三次插值，可以看出雙三次插值效果好，雙線性插值更平滑一點，清晰度不足。

3. 總結

本文介紹了三種常見的插值算法以及在數字圖像處理中的應用。總結如下：

• 線性插值：通過2點插值新的點，可以利用線性回歸計算插值點
• 雙線性插值：通過4個點插值新的點
• 雙三次插值：通過16個點插值新的點，插值權重利用bicubic函數

作者簡介：wedo實驗君, 數據分析師;熱愛生活，熱愛寫作