德國數(shù)學(xué)家大衛(wèi) · 希爾伯特（David Hilbert）是二十世紀最偉大的數(shù)學(xué)家之一，被后人稱為「數(shù)學(xué)世界的亞歷山大」。他對數(shù)學(xué)領(lǐng)域做出了廣泛和重大的貢獻，研究領(lǐng)域涉及代數(shù)不變式、代數(shù)數(shù)域、幾何基礎(chǔ)、變分法、積分方程、無窮維空間以及物理學(xué)和數(shù)學(xué)基礎(chǔ)等。1899 年出版的《幾何基礎(chǔ)》成為近代公理化方法的代表作，且由此推動形成了「數(shù)學(xué)公理化學(xué)派」。

David Hilbert。

1900 年 8 月 8 日，在法國巴黎舉辦的第二屆國際數(shù)學(xué)家大會上，大衛(wèi) · 希爾伯特提出了新世紀數(shù)學(xué)家應(yīng)當(dāng)努力解決的 23 個問題。這 23 個問題統(tǒng)稱「希爾伯特問題」，共分屬四大塊：1 至 6 屬于基礎(chǔ)數(shù)學(xué)問題，7 至 12 屬于數(shù)論問題，13 至 18 屬于代數(shù)和幾何問題，19 至 23 屬于數(shù)學(xué)分析問題。這些問題成為了后世數(shù)學(xué)家們努力攻克的難關(guān)，并對現(xiàn)代數(shù)學(xué)的研究和發(fā)展產(chǎn)生了積極和深刻的影響。

一個多世紀過去了，這些問題中的大多數(shù)得到了圓滿解決或部分解決，但有些依然未能解決，其中包括第十二個問題「一般代數(shù)數(shù)域的阿貝爾擴張（Abelian extension）」。就其定義而言，阿貝爾擴張是一類重要的域擴張，設(shè) K 是域 F 的伽羅瓦擴域，若其伽羅瓦群 G(K/F) 為一阿貝爾群，則稱此擴張為阿貝爾擴張，此時，K 稱為 F 上阿貝爾擴域。

1912 年，德國數(shù)學(xué)家埃里希 · 赫克使用希爾伯特模形式研究了實二次域的情形，虛二次域的情形用復(fù)乘理論已基本解決。一般情況下的阿貝爾擴張則尚未解決。

圖源：wikipedia。

其實，在希爾伯特提出他的 23 個問題清單前不久，數(shù)學(xué)家們就發(fā)現(xiàn)了一些與有理數(shù)相關(guān)的特定數(shù)字的構(gòu)建塊，其中這些有理數(shù)可以使用整數(shù)比例來表示。巧合的是，這一發(fā)現(xiàn)是解決第 12 個問題的基礎(chǔ)，要求尋找與有理數(shù)以外的數(shù)字系統(tǒng)相關(guān)的構(gòu)建塊。

經(jīng)過數(shù)學(xué)家們數(shù)十年不斷的研究探索，今年 3 月初發(fā)表在 arXiv 上的論文《Brumer–Stark Units and Hilbert’s 12th Problem 》終于描述出了希爾伯特 100 多年前尋找的用于廣泛數(shù)字系統(tǒng)的構(gòu)建塊，但是得出的答案依賴一些非常現(xiàn)代的觀點。

論文地址：
https://arxiv.org/pdf/2103.02516.pdf

論文作者分別是杜克大學(xué)數(shù)學(xué)系教授 Samit Dasgupta（左）和印度科學(xué)研究院數(shù)學(xué)系教授 Mahesh Kakde（右）。

對于這項研究，美國數(shù)學(xué)家、加州大學(xué)圣地亞哥分校和哈佛大學(xué)名譽教授 Benedict Gross 表示：「這是我們期待已久的事情，他們確實取得了一項重大突破。雖然與希爾伯特的想法完全不同，但這就是數(shù)學(xué)的魅力。你永遠無法預(yù)測以何種方式解決問題。」

在解讀這兩位數(shù)學(xué)家的研究成果和方法前，我們首先來了解下希爾伯特第 12 個問題的數(shù)論基礎(chǔ)以及百年來數(shù)學(xué)家們在此問題上做出的種種努力和嘗試。

數(shù)論基礎(chǔ)：表達式的根

希爾伯特第 12 個問題是建立在數(shù)論基礎(chǔ)上，是研究數(shù)字的基本算術(shù)性質(zhì)，包括多項式表達式的解，比如 x^3 + 2x − 3。特別地，數(shù)學(xué)家經(jīng)常研究這些表達式的根，使多項式等于零的 x 的值。

數(shù)論家經(jīng)常根據(jù)多項式的系數(shù)類型來分類多項式。以有理數(shù)為系數(shù)的系數(shù)相對簡單，是研究的共同目標。

「我們從有理數(shù)開始，」杜克大學(xué)的數(shù)學(xué)家 Samit Dasgupta 說，他是這項最新研究的作者之一，還有一位合作者是來自印度科學(xué)研究院數(shù)學(xué)系教授 Mahesh Kakde。并表示道：「這是數(shù)論的基本系統(tǒng)。」

有時有理系數(shù)多項式的根本身就是有理數(shù)，但情況并非總是如此。這意味著數(shù)學(xué)家想要找到所有有理數(shù)多項式的根，需要在一個展開的數(shù)系統(tǒng)中尋找：復(fù)數(shù)，包括所有有理數(shù)和實數(shù)，加上虛數(shù) i。

當(dāng)在復(fù)平面上繪制多項式的根時，實數(shù)沿著 x 軸，純虛數(shù)沿著 y 軸，某些對稱性就會出現(xiàn)。這些對稱性可以用來重新排列這些點，排列它們的位置。如果你能以任何順序應(yīng)用對稱性得到相同的結(jié)果，那么多項式是阿貝爾式的。但是如果你應(yīng)用對稱性的順序改變了結(jié)果，那么這個多項式是非阿貝爾式的。數(shù)論家對阿貝爾多項式最感興趣，同樣是因為它們的簡單性，但它們很難區(qū)分。例如，x^2− 2 是阿貝爾式的， x^3 − 2 則不是。

來自俄勒岡大學(xué)的 Ellen Eischen 說：「要想得到非阿貝爾式，你不必走得很遠。」

除了這些對稱性之外，阿貝爾多項式還有一個顯著的特點，那就是試圖用簡單而準確的術(shù)語來描述多項式的根。例如，很容易準確地描述多項式 x^2−3 的根：多項式的根是正負根 3。但是對于指數(shù)較大的復(fù)雜多項式來說，要寫出它的根是很困難的。

當(dāng)然，也有變通的辦法，「你可以用數(shù)字來近似『多項式的根』，」Eischen 說。但如果你想用一種明確的方式寫下來，只能用有限的方式來寫。

然而，具有有理系數(shù)的阿貝爾多項式是特殊的：總是可以從固定的構(gòu)建塊集合中精確地計算它們的根。這個發(fā)現(xiàn)被證明是如此的強大，它啟發(fā)了希爾伯特提出了他的第 12 個問題，而這一切都歸功于一組被稱為單位根的數(shù)字。

單位根

單位根是一個看似簡單卻非常重要的概念。數(shù)值上，它們是多項式的解，其中，變量的冪被設(shè)為 1。比如， x^5 = 1 或者 x^8 = 1。這些解是復(fù)數(shù)，它們由指數(shù)中的數(shù)字表示。例如，5 次單位根就是 x^5 = 1 的五個解。

但是單位根也可以用幾何來描述，而不用方程。如果把它們畫在復(fù)平面上，這些點都在一個半徑為 1 的圓上。如果你把圓看作一個時鐘，那么在 3 點鐘指向，你總會有一個單位根，其中 x=1，因為 1 對任何冪仍然是 1。剩下的單位根在圓的周圍等間距分布。

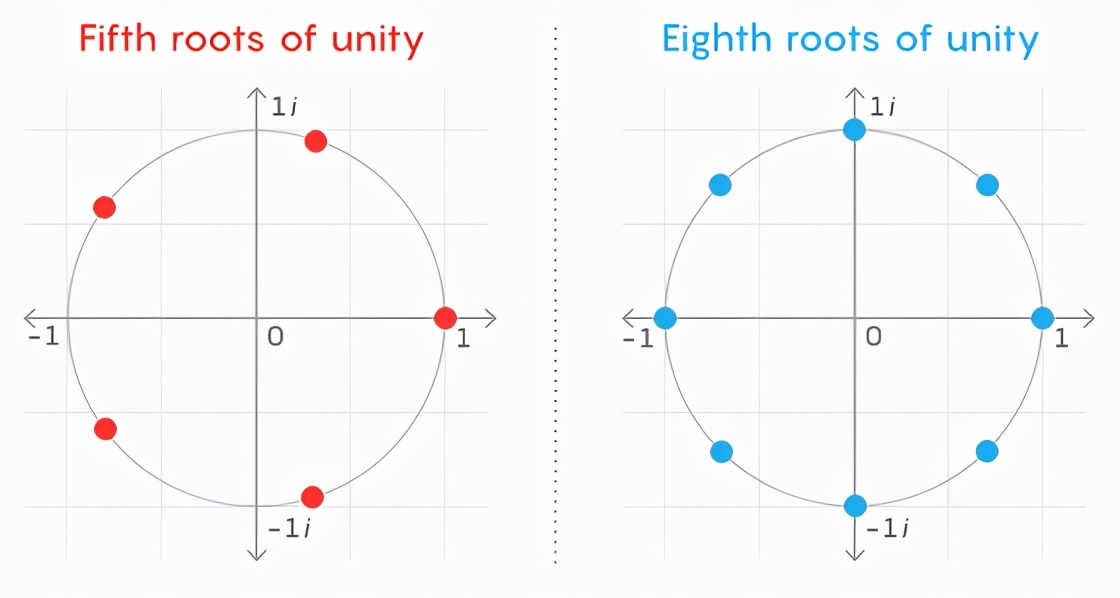
19 世紀，在希爾伯特提出數(shù)學(xué)問題清單之前，數(shù)學(xué)家們發(fā)現(xiàn)，單位根可以作為他們想要研究的特定數(shù)字集合的「構(gòu)建塊」：具有有理系數(shù)的阿貝爾多項式的根。如果你把單位根簡單地組合（用有理數(shù)加、減、乘）起來，你就能描述出所有這些期望的根。例如，5 的平方根是阿貝爾多項式 x^2-5 的根，并且可以表示為不同五次單位根的和。這與素數(shù)構(gòu)建整數(shù)塊的方式類似。

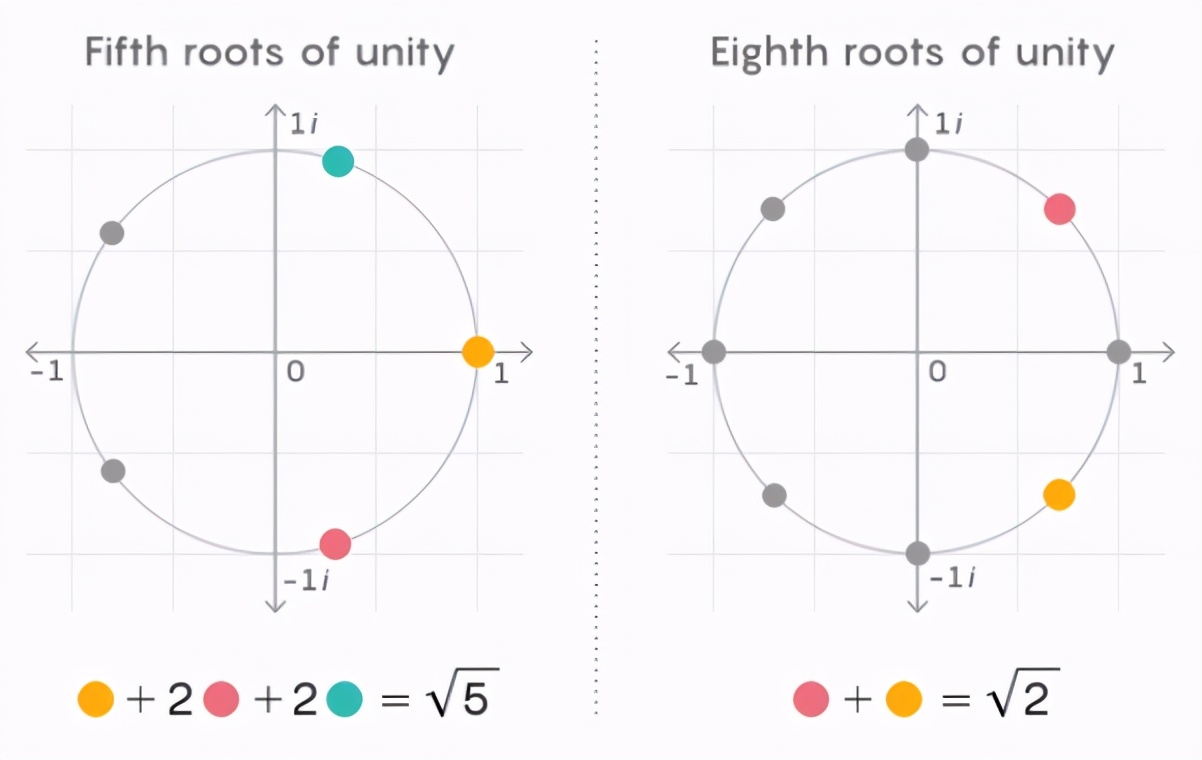
因此，單位根需要精確的構(gòu)造塊，你需要用有理系數(shù)完美地描述阿貝爾多項式的根。另一方面，任何單位根的組合都會產(chǎn)生一個數(shù)，這個數(shù)是某個有理系數(shù)阿貝爾多項式的根。這兩者有著千絲萬縷的聯(lián)系。

希爾伯特在提出他的第 12 個問題時，想要讓數(shù)學(xué)家們找到阿貝爾多項式根的構(gòu)造塊，它的系數(shù)來自有理數(shù)以外的數(shù)系統(tǒng)。換言之，對于其他數(shù)系統(tǒng)單位根有什么相似之處？

幾十年未解決的難題

這是一個雄心勃勃的問題，這也是它出現(xiàn)在希爾伯特清單上的原因。他猜想這個問題是可以回答的，因為他在提出這個問題時，就對另一種數(shù)字系統(tǒng)（稱為虛二次域）組成構(gòu)建塊的描述方式有一個構(gòu)想——大體上，該系統(tǒng)僅包含有理數(shù)和負數(shù)的平方根。幾十年后，他的猜測被證明是正確的。

倫敦帝國理工學(xué)院的 Alice Pozzi 說：「該問題有兩種情況：『有理』情況和虛二次域情況。」希爾伯特希望以與這兩種已知情況相似的方式描述其他數(shù)字系統(tǒng)的基本組成。這意味著要使用復(fù)分析（一種研究復(fù)函數(shù)的數(shù)學(xué)理論）。

但是在 20 世紀 70 年代，希爾伯特的第 12 個問題已經(jīng)提出幾十年之后，數(shù)學(xué)家 Harold Stark 猜想可以借助 L 函數(shù)破解這個問題。

L 函數(shù)是一類重要的復(fù)變數(shù)函數(shù)，通常以無窮級數(shù)表示，它是黎曼ζ函數(shù)的推廣，黎曼ζ函數(shù)如下：

幾個世紀以來，數(shù)學(xué)家都知道 L 函數(shù)是神秘并且極有意義的，它們給出了π等重要常數(shù)的無窮級數(shù)表示法。

在這種直覺的基礎(chǔ)上，Stark 能夠使用 L 函數(shù)來模擬其他數(shù)字系統(tǒng)的單位根。然而，盡管數(shù)學(xué)家認為 Stark 的猜想是正確的，并且已經(jīng)使用計算機分析法對其進行了廣泛的測試，但他們并沒有獲得任何成功的證明。

Darmon 說：「據(jù)我們所知，要證明 Stark 的猜想真的很困難，五十年來幾乎沒有任何進展。」因此，Stark 的猜想只是提供了一個簡單的思路，他猜想可以使用 L 函數(shù)從其他數(shù)字系統(tǒng)找出含系數(shù)阿貝爾多項式的根的構(gòu)建塊，但是沒人知道如何證明這一點。

更糟糕的是，Stark 的方案只提供了實際描述組成構(gòu)件塊所需要的一半信息。就像要在地圖上尋找一個位置，只提供了經(jīng)度，還需要緯度才能找到特定的地點。

20 世紀 80 年代，Benedict Gross 發(fā)表了 Stark 方案的修改版本來繼續(xù)這項數(shù)學(xué)研究。希爾伯特和 Stark 都曾考慮使用復(fù)數(shù)，而 Gross 使用了 p 進數(shù)（p-adic numbers）。

這兩種方法都是標準數(shù)字的替代方案，標準數(shù)字使用不同的方法來確定兩個數(shù)字是否接近。

Benedict Gross。

利用 p 進數(shù)可以重寫數(shù)學(xué)中的許多概念，其中包括 L 函數(shù)。實際上在現(xiàn)代數(shù)論中，p - 進 L 函數(shù)與復(fù) L 函數(shù)的關(guān)系非常密切。

即便如此，起初 Gross 將復(fù)數(shù)轉(zhuǎn)換為 p 進數(shù)似乎卻沒有讓 Stark 猜想的證明問題更進一步。在隨后的幾十年中，隨著數(shù)字理論領(lǐng)域 p 進數(shù)數(shù)論的發(fā)展，Gross 的 p 進數(shù)猜想變得容易了一些。

Darmon 說：「借助 p 進數(shù)分析能夠得到許多有趣的結(jié)果。」事實證明，相比于復(fù)數(shù)，使用 p 進數(shù)更容易解決數(shù)學(xué)中一些重要的問題，希爾伯特的第 12 個問題恰恰如此。

另辟蹊徑：計算機程序找到數(shù)字系統(tǒng)的構(gòu)建塊

今年 3 月，杜克大學(xué)教授 Samit Dasgupta 和印度科學(xué)研究院教授 Mahesh Kakde 發(fā)表的這篇論文首次使用 p - 進數(shù) L 函數(shù)回答了希爾伯特關(guān)于獨立大型數(shù)字系統(tǒng)的問題。這些數(shù)字系統(tǒng)被稱為「全實域（totally real field）」，是有理數(shù)的延伸，并包含給定多項式的一個根。

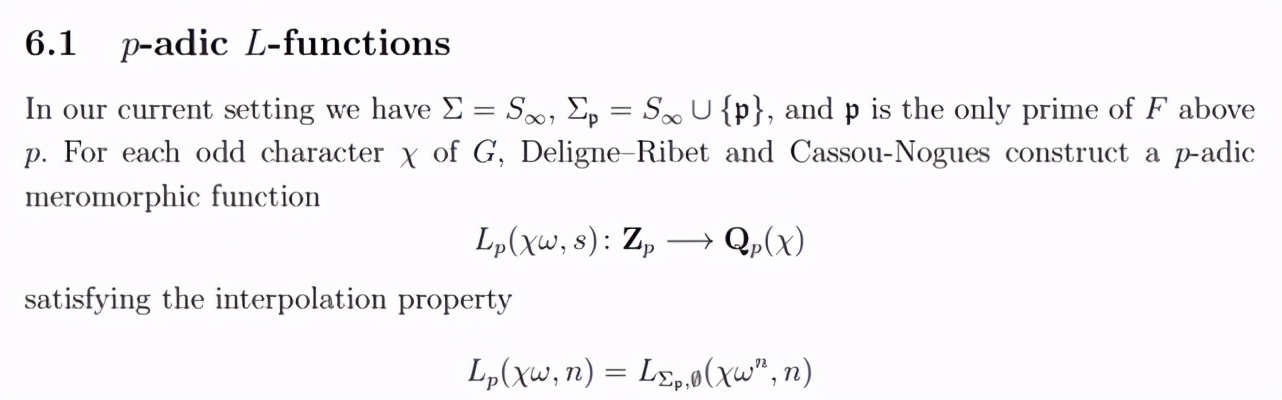
p - 進數(shù) L 函數(shù)。兩位教授通過 Deligne–Ribet 和 Cassou-Nogues 構(gòu)造了一個 p 進數(shù)亞純函數(shù)，并滿足插值性。

2004 年，Dasgupta 在其博士論文中首次提出了所需要的最終公式——對 Gross 的猜想進行了改進。此后的十年里，利用 p 進數(shù)數(shù)字理論的發(fā)展，他又先后發(fā)表兩篇論文并最終證明了 Gross 的猜想。但這還不足以解決希爾伯特的第 12 個問題，因為與 Stark 猜想一樣，Gross 的猜想只提供了精確描述構(gòu)建塊所需的兩個數(shù)字之一。

在過去的三年里，Dasgupta 和 Kakde 合作想要證明能夠提供構(gòu)建塊所需的兩個數(shù)字的 Gross 猜想，盡管看起來可能無法實現(xiàn)。

Kakde 曾說道：「我們兩人都非常樂觀。有時會遇到難以解決的障礙，但幸運的是，我們一直在取得進展。」

直到 2020 年，他們終于有了突破，證明了與全實域相關(guān)的精確構(gòu)建塊的確存在。換言之，他們知道自己想要實現(xiàn)的東西就在某個地方，并指引他們朝著正確的方向前進。他們得到了用以證明完整描述構(gòu)建塊的精確公式存在的關(guān)鍵方程式。

格羅斯猜想的部分證明步驟。

為了驗證正確性，Dasgupta 的兩名學(xué)生編寫了一個計算機程序，由此生成了用于給定數(shù)字系統(tǒng)的構(gòu)建塊，并展示了工作原理。除了理論證明之外，這個計算機程序還幫助證明了 Dasgupta 和 Kakde 提出的公式的正確性，這是解決此類抽象問題的一個重要因素。

此外，這個計算機程序在 GitHub 上有一個項目，名為「
Computation-of-Elliptic-Units」，主要計算「生成實二次域希爾伯特類域所需的橢圓形單位和多項式」。下表 1 為一部分計算結(jié)果：

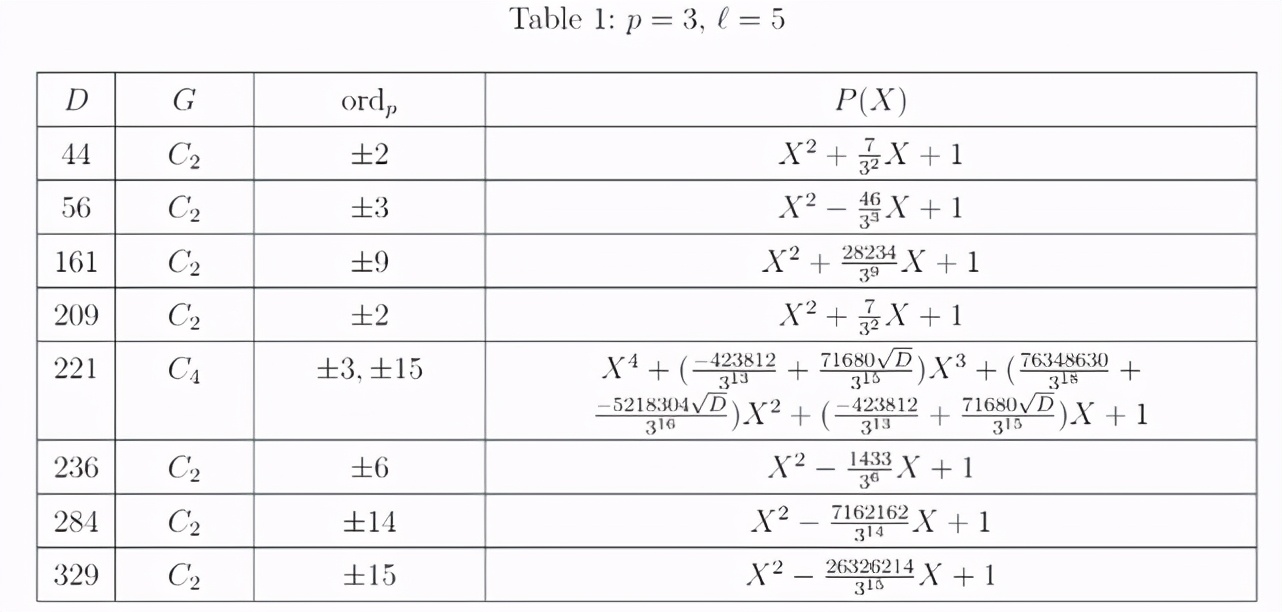
項目地址：
https://github.com/liuyj8526/Computation-of-Elliptic-Units

希爾伯特的第 12 個問題要求精確描述阿貝爾多項式的根的構(gòu)造塊，類似于單位根，Dasgupta 和 Kakde 的研究給出了一系列數(shù)字系統(tǒng)的構(gòu)造塊，盡管是以 p - 進 L 函數(shù)的形式，具有明顯的現(xiàn)代性。

但還有最后一個問題：既然希爾伯特明確地寫道，構(gòu)建塊應(yīng)該由復(fù)數(shù)組成，那么這個解偏離希爾伯特最初的指令，這顯示了數(shù)學(xué)的通用性。使用 p 進數(shù)分析為希爾伯特的問題提供了答案，但使用復(fù)分析的原始問題仍需未來的數(shù)學(xué)家探索。可能有很多方法來描述構(gòu)建塊，未來也許能夠使用復(fù)數(shù)來描述它們，從而滿足希爾伯特的最初要求。

正如 Gross 所說：「這是一場接力賽，當(dāng)你精疲力盡時把接力棒傳給下一個人。」