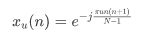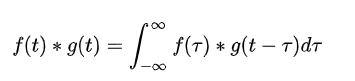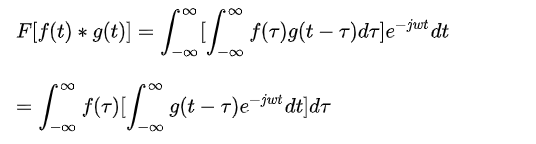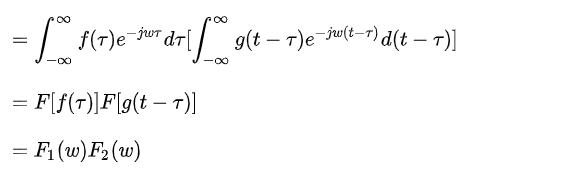在無線通信系統(tǒng)中同步是非常關(guān)鍵的一個過程，這對信號正確的傳輸有著非常的重要意義。通常，我們常用CAZAC序列(Const Amplitude Zero Auto-Corelation)進行幀同步，CAZAC序列全稱恒包絡(luò)零自相關(guān)序列。它主要包括有ZC序列、Frank序列、Golomb多相序列和Chirp序列等。因為其有很好的自相關(guān)特性，廣泛用于無線通信領(lǐng)域，雷達、CDMA、LTE、5G NR等需要進行信號同步的通信方式。

下面我們以ZC序列為例，利用Python畫圖來直觀的理解這種序列。

ZC序列全稱是Zadoff Chu序列，由于其是由Zadoff和Chu提出，所以便由他們的名字來命名，它可以用下面的公式來表示：

式中的u就是它的根。

根據(jù)ZC序列的公式，我們就可以方便的畫出ZC序列的圖形，話不多說，直接擼代碼。

u = 1 
N = 128 
n = np.arange(N) 
x = np.exp(-1j * np.pi*u*n*(n+1)/(N-1)) 
plt.subplot(2,1,1) 
plt.plot(np.real(x)) 
plt.subplot(2,1,2) 
plt.plot(np.imag(x)) 
plt.show() 

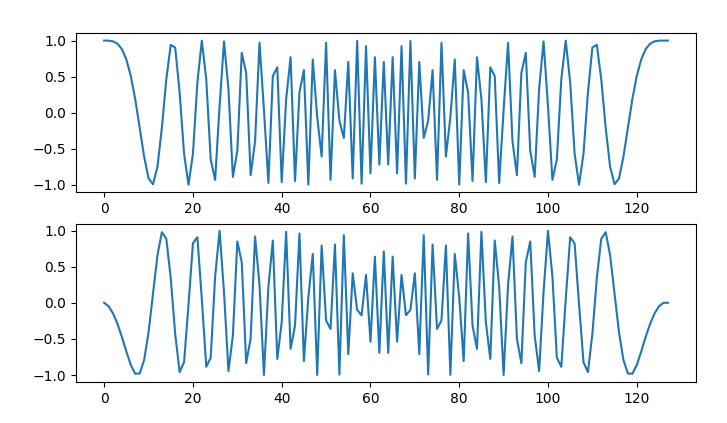
這里序列根取1，N取128，如下圖是它的時域圖形，是不是覺得上面的圖形看上去似乎有一些規(guī)則性。

ZC序列

那么，它特別的地方在哪里呀?我們可以換個角度來看這個序列，下面我們在用復(fù)數(shù)坐標(biāo)系上把這個序列畫出來看看是什么樣子。

u = 1 
N = 128 
n = np.arange(N) 
x = np.exp(-1j * np.pi*u*n*(n+1)/(N-1)) 
plt.scatter(np.real(x), np.imag(x)) 
plt.show() 

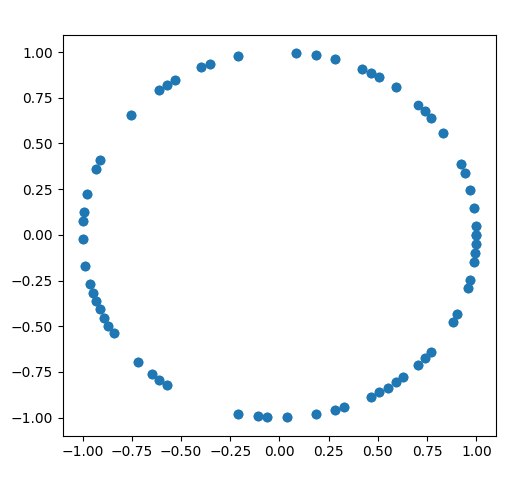
圖中橫坐標(biāo)為實部I，縱坐標(biāo)為虛部Q，從圖中我們可以看出序列在復(fù)平面上是一個圓，也就是說其幅值是恒定的。

復(fù)數(shù)坐標(biāo)系下的ZC序列

從序列的公式上看它是一個以e為底的復(fù)指數(shù)函數(shù)，所以大家可以根據(jù)之前的文章《談?wù)剼W拉公式與復(fù)指數(shù)信號》來理解。

如果把兩個序列進行相關(guān)運算會發(fā)生什么情況呢?關(guān)于相關(guān)運算實際上就是卷積運算，為了方便計算我們先將序列轉(zhuǎn)到頻域進行計算，因為對于時域上卷積運算實際就是頻域上相乘，如下卷積計算公式：

將時域進行傅立葉變換：

整理公式得：

推導(dǎo)總是一堆讓人頭大的公式，不過早就有大佬幫我們總結(jié)好了，這里大家需要記住卷積定理即可。

時域卷積定理即時域內(nèi)的卷積對應(yīng)頻域內(nèi)的乘積;頻域卷積定理即頻域內(nèi)的卷積對應(yīng)時域內(nèi)的乘積。

我們繼續(xù)看下面的代碼，我們先將序列向右循環(huán)移位10位生成一個新的序列，然后，再用移位后的序列和原序列進行相關(guān)運算。

u = 1 
N = 128 
n = np.arange(N) 
x = np.exp(-1j * np.pi*u*n*(n+1)/(N-1)) 
corr = np.fft.fftshift(np.fft.fft(x)) * np.conj(np.fft.fftshift(np.fft.fft(x))) 
plt.subplot(2,1,1) 
plt.plot(np.abs(np.fft.ifftshift(np.fft.ifft(corr)))) 
 
x_r = np.roll(x, 10) #右移 
corr = np.fft.fftshift(np.fft.fft(x_r)) * np.conj(np.fft.fftshift(np.fft.fft(x))) 
plt.subplot(2,1,2) 
plt.plot(np.abs(np.fft.ifftshift(np.fft.ifft(corr)))) 
plt.show() 

從下面的圖中可以發(fā)現(xiàn)，在做完相關(guān)運算之后會產(chǎn)生一個相關(guān)峰，而且相關(guān)峰的值非常的大，它的能量較為集中有較好的抗噪能力，除了相關(guān)峰外其他位置的相關(guān)值都為0或接近于0。而且，經(jīng)過移位后的序列和原序列進行相關(guān)運算之后，相干峰的位置也會向右偏移10位。由于這種相關(guān)特性，這里大家也應(yīng)該清楚了為什么說可以使用這種序列進行幀同步了。

相關(guān)運算

如果序列經(jīng)過傅立葉變換之后，序列的特性又會是什么樣呢?

u = 1 
N = 128 
n = np.arange(N) 
x = np.exp(-1j * np.pi*u*n*(n+1)/(N-1)) 
fft_shift = np.fft.fft(x) 
plt.subplot(2,2,1) 
plt.plot(np.real(fft_shift)) 
plt.subplot(2,2,2) 
plt.plot(np.imag(fft_shift)) 
plt.subplot(2,2,3) 
plt.scatter(np.real(fft_shift), np.imag(fft_shift)) 
 
fft_shift_r = np.roll(fft_shift, 10) #右移 
corr = np.fft.fftshift(np.fft.fft(fft_shift_r)) * np.conj(np.fft.fftshift(np.fft.fft(fft_shift))) 
plt.subplot(2,2,4) 
plt.plot(np.abs(np.fft.ifftshift(np.fft.ifft(corr)))) 
plt.show() 

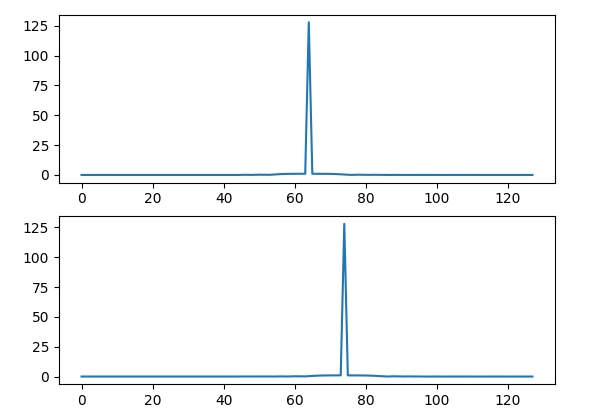
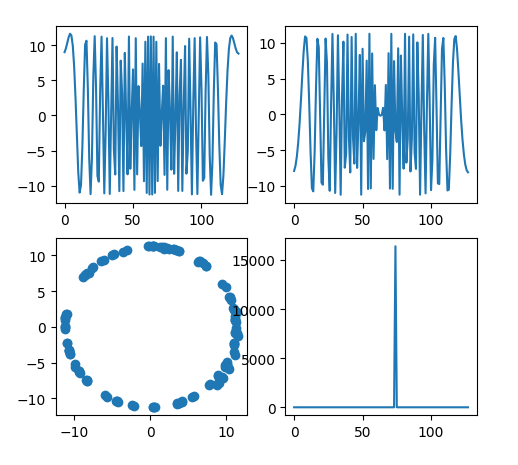
從下圖可以看出，結(jié)果顯而易見，經(jīng)過傅立葉變換之后的序列仍然具有同樣的特性。

傅立葉變換

如果不同根產(chǎn)生的ZC序列進行相關(guān)運算會發(fā)生什么情況呢?下面我們構(gòu)造兩個根為1和2的ZC序列。

u1 = 1 
u2 = 2 
N = 128 
n = np.arange(N) 
x1 = np.exp(-1j * np.pi*u1*n*(n+1)/(N-1)) 
x2 = np.exp(-1j * np.pi*u2*n*(n+1)/(N-1)) 
 
corr = np.fft.fftshift(np.fft.fft(x2)) * np.conj(np.fft.fftshift(np.fft.fft(x1))) 
plt.plot(np.abs(np.abs(np.fft.ifftshift(np.fft.ifft(corr))))) 
plt.show() 

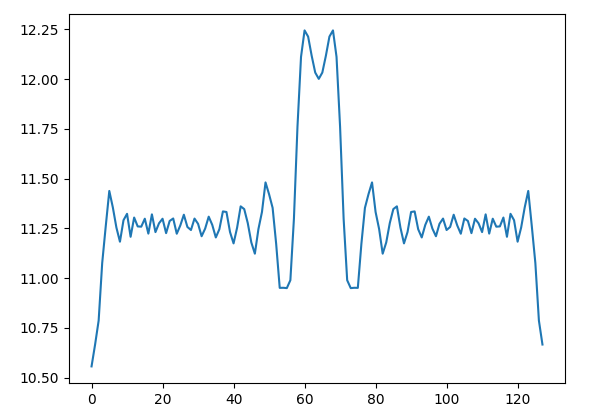
兩個不同根序列相關(guān)運算后的結(jié)果如下圖：

不同根序列相關(guān)運算

我們從圖上看出，對于不同根的序列再進行相關(guān)運算之后，不會產(chǎn)生像上面相同根的序列那樣會產(chǎn)生又高又細的相關(guān)峰。

好了，相信看了上面的幾個仿真實驗大家都對CAZAC序列有一定的認(rèn)識。信號處理一個非常抽象的技術(shù)，但是大家不要害怕，我們平時需要多多進行實驗和練習(xí)，才能慢慢的掌握它。

本文轉(zhuǎn)載自微信公眾號「Will的大食堂」，可以通過以下二維碼關(guān)注。轉(zhuǎn)載本文請聯(lián)系Will的大食堂公眾號。