7種機(jī)器學(xué)習(xí)算法的7個(gè)關(guān)鍵點(diǎn)
借助各種庫和框架,我們僅需一行代碼即可實(shí)現(xiàn)機(jī)器學(xué)習(xí)算法。有些更進(jìn)一步,使您可以立即實(shí)現(xiàn)和比較多種算法。
易用性具有一些缺點(diǎn)。我們可能會忽略這些算法背后的關(guān)鍵概念或想法,而這些概念或想法對于全面了解它們至關(guān)重要。
在這篇文章中,我將提到有關(guān)7種機(jī)器學(xué)習(xí)算法的7個(gè)關(guān)鍵點(diǎn)。我想指出的是,這不會完全解釋這些算法,因此,如果您對它們有基本的了解,那就更好了。
開始吧。
1. 支持向量機(jī)(SVM)
關(guān)鍵點(diǎn):C參數(shù)
SVM創(chuàng)建一個(gè)決策邊界,以區(qū)分兩個(gè)或多個(gè)類。
軟裕量支持向量機(jī)嘗試解決具有以下目標(biāo)的優(yōu)化問題:
- 增加決策邊界與類(或支持向量)的距離
- 最大化在訓(xùn)練集中正確分類的點(diǎn)數(shù)
這兩個(gè)目標(biāo)之間顯然需要權(quán)衡取舍。決策邊界可能必須非常接近某一特定類才能正確標(biāo)記所有數(shù)據(jù)點(diǎn)。但是,在這種情況下,由于決策邊界對噪聲和自變量的微小變化過于敏感,因此新觀測值的準(zhǔn)確性可能會降低。
另一方面,可能會為每個(gè)類別設(shè)置盡可能大的決策邊界,但要付出一些錯(cuò)誤分類的例外的代價(jià)。這種權(quán)衡由c參數(shù)控制。
C參數(shù)為每個(gè)錯(cuò)誤分類的數(shù)據(jù)點(diǎn)增加了懲罰。如果c小,則對錯(cuò)誤分類的點(diǎn)的懲罰較低,因此以較大數(shù)量的錯(cuò)誤分類為代價(jià)選擇了具有較大余量的決策邊界。
如果c大,由于高罰分,SVM會嘗試最大程度地減少誤分類示例的數(shù)量,從而導(dǎo)致決策邊界的邊距較小。對于所有錯(cuò)誤分類的示例,懲罰都不相同。它與到?jīng)Q策邊界的距離成正比。
2. 決策樹
關(guān)鍵點(diǎn):信息獲取
選擇要分割的特征時(shí),決策樹算法會嘗試實(shí)現(xiàn):
- 更具預(yù)測性
- 雜質(zhì)少
- 較低的熵
熵是不確定性或隨機(jī)性的量度。變量具有的隨機(jī)性越多,熵就越高。具有均勻分布的變量具有最高的熵。例如,擲骰子有6個(gè)概率相等的可能結(jié)果,因此它具有均勻的分布和較高的熵。
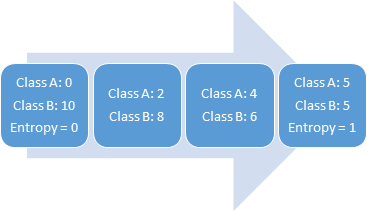
> Entropy vs Randomness
選擇導(dǎo)致更多純節(jié)點(diǎn)的拆分。所有這些都表明"信息增益",基本上是分裂前后的熵之差。
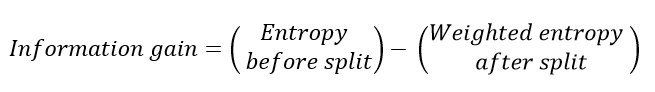
3. 隨機(jī)森林
關(guān)鍵點(diǎn):自舉和功能隨機(jī)性
隨機(jī)森林是許多決策樹的集合。隨機(jī)森林的成功很大程度上取決于使用不相關(guān)的決策樹。如果我們使用相同或非常相似的樹,則總體結(jié)果將與單個(gè)決策樹的結(jié)果相差無幾。隨機(jī)森林通過自舉和特征隨機(jī)性來實(shí)現(xiàn)具有不相關(guān)的決策樹。
自舉是從訓(xùn)練數(shù)據(jù)中隨機(jī)選擇樣本進(jìn)行替換。它們稱為引導(dǎo)程序樣本。
通過為隨機(jī)森林中的每個(gè)決策樹隨機(jī)選擇特征來實(shí)現(xiàn)特征隨機(jī)性。可以通過max_features參數(shù)控制用于隨機(jī)森林中每棵樹的特征數(shù)量。

> Feature randomness
4. 梯度提升決策樹
關(guān)鍵點(diǎn):學(xué)習(xí)率和n_estimators
GBDT是決策樹與boosting方法的結(jié)合體,意味著決策樹是順序連接的。
學(xué)習(xí)率和n_estimator是用于梯度提升決策樹的兩個(gè)關(guān)鍵超參數(shù)。
學(xué)習(xí)率僅表示模型學(xué)習(xí)的速度。學(xué)習(xí)速度較慢的優(yōu)點(diǎn)是模型變得更健壯和更通用。但是,學(xué)習(xí)緩慢需要付出一定的代價(jià)。訓(xùn)練模型需要更多時(shí)間,這將我們帶到另一個(gè)重要的超參數(shù)。
n_estimator參數(shù)是模型中使用的樹數(shù)。如果學(xué)習(xí)率低,我們需要更多的樹來訓(xùn)練模型。但是,我們在選擇樹數(shù)時(shí)需要非常小心。使用過多樹木會產(chǎn)生過度擬合的高風(fēng)險(xiǎn)。
5. 樸素貝葉斯分類器
關(guān)鍵點(diǎn):樸素假設(shè)有什么好處?
樸素貝葉斯(Naive Bayes)是一種用于分類的監(jiān)督式機(jī)器學(xué)習(xí)算法,因此任務(wù)是在給定要素值的情況下找到觀測的類別。樸素貝葉斯分類器在給定一組特征值(即p(yi | x1,x2,…,xn))的情況下計(jì)算類的概率。
樸素貝葉斯假設(shè)要素彼此獨(dú)立,要素之間沒有關(guān)聯(lián)。但是,現(xiàn)實(shí)生活中并非如此。特征不相關(guān)的這種天真假設(shè)是將該算法稱為"天真"的原因。
與復(fù)雜算法相比,所有功能都是獨(dú)立的這一假設(shè)使其變得非常快。在某些情況下,速度比精度更高。
它適用于高維數(shù)據(jù),例如文本分類,電子郵件垃圾郵件檢測。
6. K最近鄰居
關(guān)鍵點(diǎn):何時(shí)使用和不使用
K近鄰(kNN)是一種受監(jiān)督的機(jī)器學(xué)習(xí)算法,可用于解決分類和回歸任務(wù)。kNN的主要原理是,數(shù)據(jù)點(diǎn)的值由其周圍的數(shù)據(jù)點(diǎn)確定。
隨著數(shù)據(jù)點(diǎn)數(shù)量的增加,kNN算法變得非常慢,因?yàn)槟P托枰鎯λ袛?shù)據(jù)點(diǎn)以便計(jì)算它們之間的距離。這個(gè)原因也使該算法的存儲效率不高。
另一個(gè)缺點(diǎn)是kNN對異常值敏感,因?yàn)楫惓V禃绊懽罱狞c(diǎn)(即使距離太遠(yuǎn))。
在積極方面:
- 簡單易懂
- 不做任何假設(shè),因此可以在非線性任務(wù)中實(shí)施。
- 在多個(gè)類別的分類上效果很好
- 適用于分類和回歸任務(wù)
7. K-Means聚類
關(guān)鍵點(diǎn):何時(shí)使用和不使用
K-均值聚類旨在將數(shù)據(jù)劃分為k個(gè)聚類,以使同一聚類中的數(shù)據(jù)點(diǎn)相似,而不同聚類中的數(shù)據(jù)點(diǎn)相距更遠(yuǎn)。
K-均值算法無法猜測數(shù)據(jù)中存在多少個(gè)簇。群集的數(shù)量必須預(yù)先確定,這可能是一項(xiàng)艱巨的任務(wù)。
該算法隨著樣本數(shù)量的增加而減慢速度,因?yàn)樵诿總€(gè)步驟中,它都會訪問所有數(shù)據(jù)點(diǎn)并計(jì)算距離。
K均值只能繪制線性邊界。如果存在將數(shù)據(jù)中的組分開的非線性結(jié)構(gòu),則k均值將不是一個(gè)很好的選擇。
在積極方面:
- 容易解釋
- 比較快
- 可擴(kuò)展用于大型數(shù)據(jù)集
- 能夠以智能方式選擇初始質(zhì)心的位置,從而加快收斂速度
- 保證融合
我們已經(jīng)介紹了有關(guān)每種算法的一些關(guān)鍵概念。給出的要點(diǎn)和注釋絕對不是算法的完整說明。但是,了解實(shí)現(xiàn)這些算法時(shí)必須有所作為當(dāng)然很重要。

























