面試官本想拿一道求素數搞我,但被我優雅的"回擊"了
本文轉載自微信公眾號「 bigsai」,作者 bigsai。轉載本文請聯系 bigsai公眾號。
前言
現在的面試官,是無數開發者的夢魘,能夠吊打面試官的屬實不多,因為大部分面試官真的有那么那幾下子。但在面試中,我們這些小生存者不能全盤否定只能單點突破—從某個問題上讓面試官眼前一亮。這不,今天就來分享來了。
這年頭,算法崗內卷不說,開發崗也有點內卷,對開發者要求越來越高了,而面試官也是處心積慮的 "刁難" 面試者,凡是都喜歡由淺入深,凡是都喜歡問個:你知道為什么?你知道原理嗎?之類。并且,以前只是大廠面試官喜歡問算法,大廠員工底子好,很多甚至有ACM經驗或者系統刷題經驗,這很容易理解,但現在一些小公司面試官也是張口閉口 xx算法、xx數據結構你說說看,這不,真的被問到了。
求一個質數
在這么一次的過程,面試官問我算法題我不吃驚,我實現早把十大排序原理、復雜度分析、代碼手寫實現出來了,也把鏈表、樹的各種操作溫習的滾瓜爛熟,不過突然就是很詫異的面試官來了一道求素數問題,我把場景還原一下:
面試官:你知道怎么求素數嗎?
我:求素數?
面試官:是的,就是求素數。
我:這很簡單啊,判斷一個數為素數,那么肯定就沒有兩個數(除了自身和1)相乘等于它,只需要枚舉看看有沒有能夠被它整除的數就可以了,如果有那么就不是素數,如果沒有,那么就是素數。
面試官露出一種失望的表情,說我說的對,但沒答到點子上,讓我具體說一下。
下面開始開始我的表演:
首先,最笨的方法,判斷n是否為素數,就是枚舉[2,n-1]之間有沒有直接能夠被n整除的,如果有,那么返回false這個就不是素數,否則就是素數,代碼如下:
- boolean isprime(int value){
- for(int i=2;i<value;i++)
- {
- if(value%i==0)
- {return false;}
- }
- return true;
- }
這種判斷一個素數的時間復雜度為O(n).
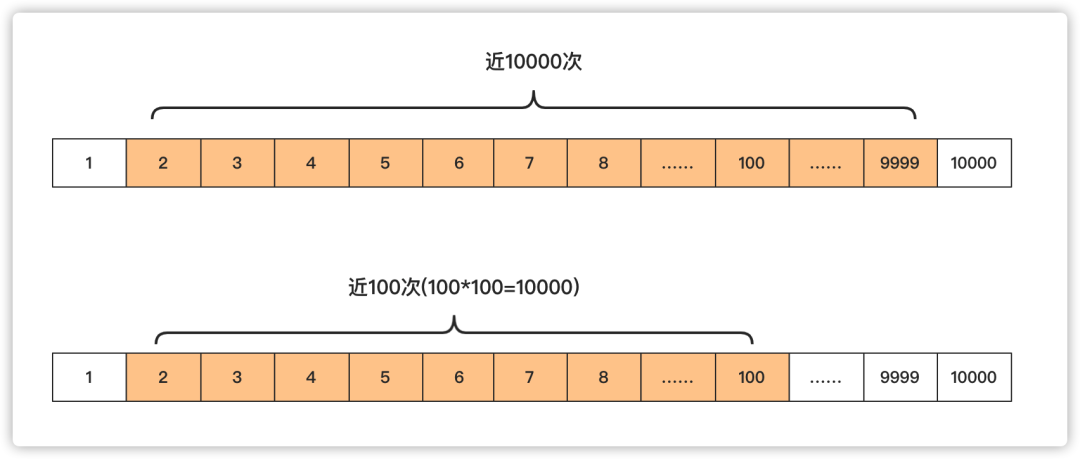
但是其實這種太浪費時間了,完全沒必要這樣,可以優化一下 。如果一個數不是質數,那么必定是兩個數的乘積,而這兩個數通常一個大一個小,并且小的小于等于根號n,大的大于等于根號n,我們只需要枚舉小的可能范圍,看看是否能夠被整除,就可以判斷這個數是否為素數啦。例如100=2*50=4*25=5*20=10*10 只需要找2—10這個區間即可。右側的一定有個對應的不需要管它。
- boolean isprime(int value)
- {
- for(int i=2;i*i<value+1;i++)
- {
- if(value%i==0)
- {return false;}
- }
- return true;
- }
這里之所以要小于value+1,就是要包含根號的情況,例如 3*3=9.要包含3.這種時間復雜度求單個數是O(logn)。面試官我給你畫張圖讓你看看其中區別:
2
說到這里面試官露出欣慰的笑容。
面試官:不錯不錯,基本點掌握了
我:老哥,其實求素數精髓不在這,這個太低效在很多時候,比如求小于n的所有素數,你看看怎么搞?
面試官:用個數組用第二種方法求nlogn還行啊。
求多個素數
求多個素數的時候(小于n的素數),上面的方法就很繁瑣了,因為有大量重復計算,因為 計算某個數的倍數 是否為素數的時候出現大量的重復計算,如果這個數比較大那么對空間浪費比較多。
這樣,素數篩的概念就被發明和使用。篩的原理是從前往后進行一種遞推、過濾排序以來統計素數。
埃拉托斯特尼(Eratosthenes)篩法
我們看一個數如果不是為素數,那么這個數沒有數的乘積能為它,那么這樣我們可以根據這個思想進行操作啊:
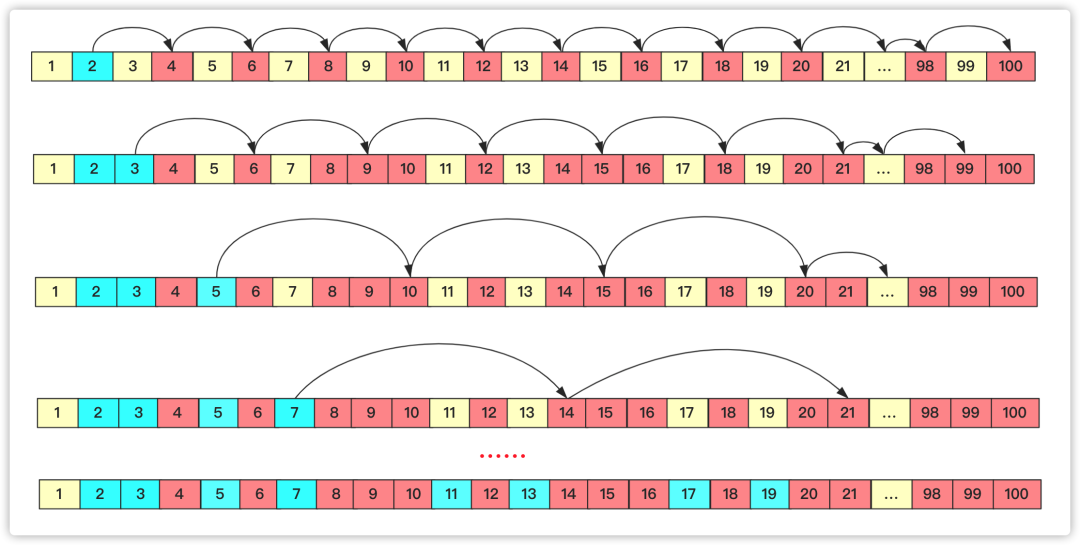
直接從前往后枚舉,這個數位置沒被標記的肯定就是素數,如果這個數是素數那么將這個數的倍數標記一下(下次遍歷到就不需要在計算)。如果不是素數那么就進行下一步。這樣數值越大后面計算次數越少,在進行具體操作時候可借助數組進行判斷。所以埃氏篩的核心思想就是將素數的倍數確定為合數。
假設剛開始全是素數,2為素數,那么2的倍數均不是素數;然后遍歷到3,3的倍數標記一下;下個是5(因為4已經被標記過);一直到n-1為止。具體流程可以看圖:
具體代碼為:
- boolean isprime[];
- long prime[];
- void getprime()
- {
- prime=new long[100001];//記錄第幾個prime
- int index=0;//標記prime當前下標
- isprime=new boolean [1000001];//判斷是否被標記過
- for(int i=2;i<1000001;i++)
- {
- if(!isprime[i])
- {
- prime[index++]=i;
- }
- for(int j=i+i;j<1000000;j=j+i)//他的所有倍數都over
- {
- isprime[j]=true;
- }
- }
- }
這種篩的算法復雜度為O(nloglogn);別小瞧多的這個logn,數據量大一個log可能少不少個0,那時間也是十倍百倍甚至更多的差距。
歐拉篩
面試官已經開始點頭贊同了,哦哦的叫了起來,可其實還沒完。還有個線性篩—歐拉篩。觀察上述的埃氏篩,有很多重復的計算,尤其是前面的素數,比如2和3的最小公倍數為6,每3次2的計算就也會遇到是3的倍數,而歐拉篩在埃氏篩的基礎上改進,有效的避免了這個重復計算。
具體是何種思路呢?就是埃氏篩是遇到一個質數將它的倍數計算到底,而歐拉篩則是只用它乘以已知曉的素數的乘積進行標記,如果素數能夠被整除那就停止往后標記。
在實現上同樣也是用兩個數組,一個存儲真實有效的素數,一個用來作為標記使用。
- 在遍歷到一個數的時候,如果這個數沒被標記,那么這個數存在素數的數組中,對應下標加1.
- 不管這個數是不是素數,遍歷已知素數將它和該素數的乘積值標記,如果這個素數能夠被當前值i整除,那么停止操作進行下一輪。
具體實現的代碼為:
- boolean isprime[];
- int prime[];
- void getprimeoula()// 歐拉篩
- {
- prime = new int[100001];// 記錄第幾個prime
- int index = 0;
- isprime = new boolean[1000001];
- for (int i = 2; i < 1000001; i++) {
- if (!isprime[i]) {
- prime[index++] = i;
- }
- for (int j = 0; j < index && i * prime[j] <= 100000; j++){//已知素數范圍內枚舉
- isprime[i * prime[j]] = true;// 標記乘積
- if (i % prime[j] == 0)
- break;
- }
- }
- }
你可能會問為啥if (i % prime[j] == 0)就要break。
如果i%prime[j]==0,那么就說明i=prime[j]*k. k為一個整數。
那么如果進行下一輪的話
i*prime[j+1]=(prime[j]*k)*prime[j+1]=prime[j]*(k*prime[j+1]) 當i=k*prime[j+1]兩個位置就產生沖突重復計算啦,所以一旦遇到能夠被整除的就停止。
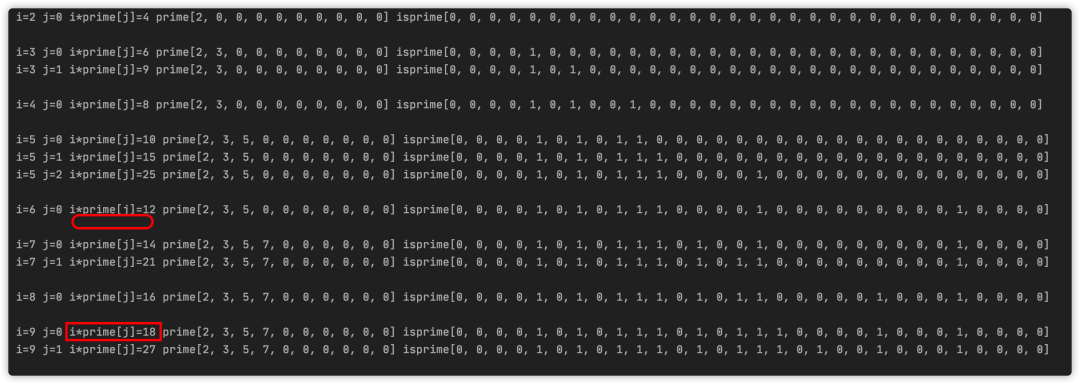
image-20201208121324157
你可以看到這個過程,6只標記12而不標記18,18被9*2標記。詳細理解還需要多看看代碼想想。過程圖就不畫啦!歐拉的思路就是離我較近的我給它標記。歐拉篩的時間復雜度為O(n),因為每個數只標記一次。
面試官露出一臉欣賞的表情,說了句不錯,下面就是聊聊家常,讓我等待下一次面試!