微軟AI要參加IMO競(jìng)賽!小目標(biāo):數(shù)學(xué)金牌
本文經(jīng)AI新媒體量子位(公眾號(hào)ID:QbitAI)授權(quán)轉(zhuǎn)載,轉(zhuǎn)載請(qǐng)聯(lián)系出處。
今年,可能是最后一屆“純?nèi)祟?rdquo;參賽的IMO (國(guó)際奧數(shù)競(jìng)賽)。

△參加2020年IMO的中國(guó)代表隊(duì)(李金珉的官方年齡信息有誤)
因?yàn)樵诿髂辏珹I可能也會(huì)加入這場(chǎng)金牌爭(zhēng)奪戰(zhàn)中,成為一名“種子選手”。
這名潛入IMO賽事的AI名為Lean,由微軟的研究人員開(kāi)發(fā)。
目前,他們正計(jì)劃讓Lean參與明年的國(guó)際奧數(shù)競(jìng)賽。
也就是說(shuō),它將與世界各國(guó)的奧賽選手一起爭(zhēng)奪IMO金牌。
準(zhǔn)備在IMO上一展身手的Lean
其實(shí),微軟研究人員讓AI參加IMO的理由,原因是它是個(gè)很好的實(shí)驗(yàn)工具(工具人)。
微軟研究員Selsam是挑戰(zhàn)賽IMO Grand Challenge的創(chuàng)始人之一,他表示,這項(xiàng)比賽的目的是訓(xùn)練一個(gè)人工智能系統(tǒng),以便在世界頂級(jí)數(shù)學(xué)競(jìng)賽中贏得金牌。
因?yàn)檫@里不僅有數(shù)學(xué)上“最簡(jiǎn)單”的難題(連高等數(shù)學(xué)都用不上,但就是做不出來(lái)),而且還匯集了來(lái)自世界各地的頂尖高手。
如果AI能像人一樣證明這些數(shù)學(xué)定理,某種程度上也能說(shuō)明,讓它“像人一樣思考”不會(huì)太過(guò)困難。
基于這個(gè)想法,微軟的研究人員從2013年開(kāi)始研發(fā)Lean,希望讓AI能擁有自主判斷、根據(jù)假設(shè)進(jìn)行演繹的能力。
也就是說(shuō),它是個(gè)旨在縮小交互式定理證明、與自動(dòng)定理證明之間的差距的開(kāi)源項(xiàng)目。
自動(dòng)定理證明:對(duì)數(shù)學(xué)中提出的定理或猜想,尋找一種證明或反證的方法。系統(tǒng)不僅能根據(jù)假設(shè)進(jìn)行演繹,還要有一定的判定技巧。
交互式定理證明:借助計(jì)算機(jī)輔助證明工具,理解檢驗(yàn)數(shù)學(xué)定理正確性,完成數(shù)學(xué)定理的證明。
Lean已經(jīng)推出了3個(gè)版本,現(xiàn)在的第四個(gè)版本Lean 4還在完善中,現(xiàn)在的邏輯系統(tǒng)基于依賴類型理論,已經(jīng)強(qiáng)大到足以證明所有的常規(guī)數(shù)學(xué)定理。
也就是說(shuō),想要讓它自己證明IMO中提出來(lái)的、此前“沒(méi)見(jiàn)過(guò)的”數(shù)學(xué)問(wèn)題,依舊非常困難。
目前,Lean 4還沒(méi)有徹底做好準(zhǔn)備,作者Leonardo de Moura表示,如果讓它參加今年的IMO,“可能只能得0分”。
因?yàn)椋琇ean目前甚至無(wú)法理解某些數(shù)學(xué)問(wèn)題需要涉及哪些概念,而這些概念本身又是“什么意思”。
證明的“第一步”,就難住了算法
對(duì)于不少人來(lái)說(shuō),數(shù)學(xué)十分抽象、難以學(xué)好。
事實(shí)上,AI和你的感覺(jué)一樣。
一般的工程應(yīng)用問(wèn)題中,AI得心應(yīng)手,因?yàn)樵陬A(yù)訓(xùn)練階段,算法模型已經(jīng)對(duì)一類問(wèn)題有所了解。
也就是說(shuō),AI現(xiàn)階段能干的活仍然有限,通常要給定條件和數(shù)據(jù),經(jīng)過(guò)持續(xù)的“刷題”,才能做“更復(fù)雜的計(jì)算”。
這是一個(gè)從“1”到“2”、“3”,甚至是無(wú)窮的過(guò)程。

但數(shù)學(xué)問(wèn)題的證明本質(zhì)并不一樣,證明一個(gè)公理,或是一個(gè)復(fù)雜的等式,需要完全“白手起家”。
證明的第一步:提出一個(gè)合理證明路徑。這個(gè)從0到1的關(guān)鍵,目前只有人類的大腦能勝任。
絕大部分AI,很難給出證明思路的第一步。
拿一個(gè)最簡(jiǎn)單最古老的數(shù)學(xué)公理來(lái)說(shuō),公元前300年,歐幾里得就證明了質(zhì)數(shù)有無(wú)限多個(gè)。
而要證明這一結(jié)論,關(guān)鍵是要認(rèn)識(shí)到,總是可以通過(guò)乘所有已知的質(zhì)數(shù)并加1來(lái)找到一個(gè)新的質(zhì)數(shù)。有了這個(gè)思路,接下來(lái)的證明就很簡(jiǎn)單了。
但“想到這個(gè)思路”這一行為本身,對(duì)于AI來(lái)說(shuō),難度巨大。
說(shuō)回IMO,正式比賽中的3道題目,盡管不涉及微積分等高等數(shù)學(xué),但無(wú)一不是要求選手利用中學(xué)的所有數(shù)學(xué)知識(shí),進(jìn)行巧妙的構(gòu)思給出解題方法。
比如這道2005年IMO真題:
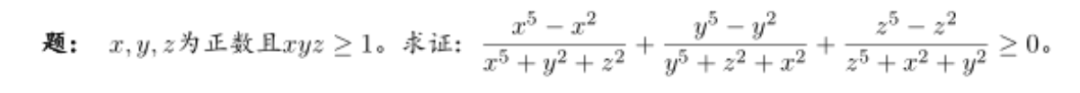
當(dāng)時(shí)不同國(guó)家的參賽選手至少給出了3種不同的證明,其中被廣泛認(rèn)可討論的解法,采用柯西不等式簡(jiǎn)化的思路,篇幅大概需要半頁(yè)A4紙。
而另一位來(lái)自摩爾多瓦的選手,極富創(chuàng)造性的用兩行式子完成了證明:
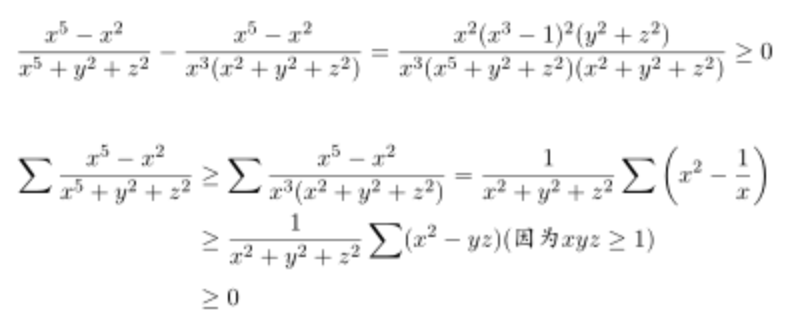
上面一行是“因?yàn)?rdquo;,下面一行就是“所以”,其簡(jiǎn)潔、精準(zhǔn)甚至可以說(shuō)“粗暴有效”震驚全場(chǎng)。
精巧的思路也獲得了當(dāng)年的IMO特別獎(jiǎng)。
要說(shuō)明的是,IMO特別獎(jiǎng)不看總成績(jī),只頒給解題方法獨(dú)到的選手。
這種石破天驚的“第一步”,對(duì)于現(xiàn)在的AI來(lái)說(shuō),幾乎是不可能做到的。
這也許就是為什么微軟的研究人員設(shè)定的目標(biāo)是“沖擊金獎(jiǎng)”吧。
巧的玩不轉(zhuǎn),Lean采取什么方法跟人類大腦競(jìng)爭(zhēng)呢?
Lean如何學(xué)數(shù)學(xué)?
Lean和所有AI算法一樣,需要“喂數(shù)據(jù)”進(jìn)行訓(xùn)練。
目前的Lean,不但無(wú)法設(shè)計(jì)出完整的IMO題目證明過(guò)程,它甚至無(wú)法理解其中一些問(wèn)題所涉及的概念。
所以,Lean的首要任務(wù)是學(xué)習(xí)更多的數(shù)學(xué)知識(shí)。
訓(xùn)練數(shù)據(jù)來(lái)自Mathlib的庫(kù)。Mathlib是一個(gè)數(shù)學(xué)基礎(chǔ)數(shù)據(jù)庫(kù),它幾乎包含了大學(xué)二年級(jí)以下所有數(shù)學(xué)知識(shí)。
但Mathlib在中學(xué)數(shù)學(xué)上仍有一些差距,團(tuán)隊(duì)正在對(duì)Mathlib數(shù)據(jù)庫(kù)進(jìn)行補(bǔ)全。
掌握知識(shí)只是第一步,如何靈活運(yùn)用才是關(guān)鍵。
團(tuán)隊(duì)采取的方法與象棋、圍棋AI等相同——遵循決策樹(shù),直到算法找到最優(yōu)解。
許多IMO題目的關(guān)鍵是尋找某種證明的模式。深入數(shù)學(xué)證明的底層,是一系列非常具體的、有邏輯的步驟。
研究人員嘗試通過(guò)IMO題目證明的全部細(xì)節(jié)來(lái)訓(xùn)練Lean。
但在這種方法也有局限,每個(gè)特定的題目證明對(duì)于算法來(lái)說(shuō)太“專”,下一個(gè)不同類型題目仍然不會(huì)解。
為了解決這個(gè)問(wèn)題,團(tuán)隊(duì)需要數(shù)學(xué)家寫(xiě)出之前IMO題目的詳細(xì)形式化證明。然后,團(tuán)隊(duì)提煉證明中的采用的不同策略。
接下來(lái),Lean的任務(wù),就是在這些策略中尋找一個(gè) “勝利 “的組合。
這項(xiàng)任務(wù)實(shí)際上比描述起來(lái)困難的多,團(tuán)隊(duì)這樣比喻它:
在圍棋中,目標(biāo)是找到最好的一步棋。而在數(shù)學(xué)中,目標(biāo)是找到最好的一盤(pán)棋,然后在這盤(pán)棋中找到最好的一步棋。
團(tuán)隊(duì)說(shuō),也許到了明年,獲得金牌仍然是很困難的,但至少,Lean有機(jī)會(huì)參賽了。
對(duì)此,有網(wǎng)友感嘆AI這些年神速的進(jìn)展:先是國(guó)際象棋、又是圍棋……現(xiàn)在,AI又要來(lái)攻占國(guó)際奧賽金牌了。

但也有網(wǎng)友持悲觀態(tài)度,認(rèn)為AI現(xiàn)階段只能在某些方面趨近人類的水平。

目前AI的算法,都是建立在人類認(rèn)知基礎(chǔ)上的……所以像(證明數(shù)學(xué)定理)這樣特殊的任務(wù),我持消極態(tài)度,畢竟世界上只有少部分人能提供幫助。
“什么是數(shù)學(xué)思想?”
這個(gè)問(wèn)題出乎意料的難以解釋透徹。數(shù)學(xué)家在嘗試解決新問(wèn)題時(shí),大腦的活動(dòng)是難以描述的,更不要說(shuō)落實(shí)在算法上。
盡管已經(jīng)有AI團(tuán)隊(duì)朝數(shù)學(xué)思想的深層邁出了一步,但是從他們采取的策略來(lái)看,仍然是學(xué)習(xí)過(guò)往思路,選擇成功率最高的“排列組合”。
這樣的AI算法,要在創(chuàng)造力和突破性上超越人類,“火候”還差得遠(yuǎn)。
而隔壁的GPT,也在數(shù)學(xué)證明方向上取得了初步成果。
最近,OpenAI推出了用于數(shù)學(xué)問(wèn)題的GPT-f,利用基于Transformer語(yǔ)言模型的生成能力進(jìn)行自動(dòng)定理證明。

由GPT-f發(fā)現(xiàn)的23個(gè)簡(jiǎn)短證明已被Metamath主庫(kù)接收,這也是首次AI的數(shù)學(xué)證明獲得業(yè)內(nèi)認(rèn)可。
GPT真的是要砸所有人的飯碗,連數(shù)學(xué)家都不放過(guò)。
那么,Lean和GPT-f,你更看好哪一個(gè)呢?
項(xiàng)目鏈接:
https://leanprover.github.io/
在線可玩:
https://leanprover.github.io/live/master/








































