數據可視化原理

幾個世紀以前，科學家沒有用相機在顯微鏡下拍攝遙遠星系或微小細菌的照片。 圖紙是傳達觀察，思想甚至理論的主要媒介。 實際上，對于科學家來說，能夠繪制抽象思想和物體的能力是一項必不可少的技能(請查看William Playfair從1700年代開始的收藏)。

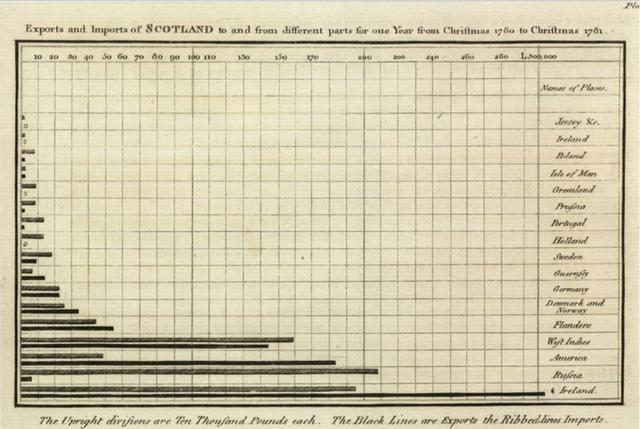
> A bar chart showing exports and imports of Scotland (William Playfair: public domain)

情況仍然如此。 我們無法拍攝分布變量或其相關性的照片。 相反，我們通過現代工具和技術通過圖紙和插圖(也稱為數據可視化)進行交流。

數據集包含一個或多個變量，我們可以通過多種方式可視化每個變量及其與其他變量的交互。 選擇哪種可視化取決于數據和我們要交流的信息類型。 但是，從根本上講，它們分為四種不同的類型：

• 單個變量的分布
• 兩個變量之間的關系
• 一個或多個變量的組成
• 不同類別/個人之間的比較

在本文中，我將通過插圖分解這四個數據可視化的基石。

1)分布

統計和數據科學中的一個重要概念是分布。 分布通常是指結果發生的可能性。 在分配100張硬幣的情況下，會有多少正面和反面? 這樣的頻率分布以直方圖或曲線表示。

下面是游泳課中學生身高分布的示意圖。 x軸顯示不同的身高類別，y軸顯示每個類別的學生人數。

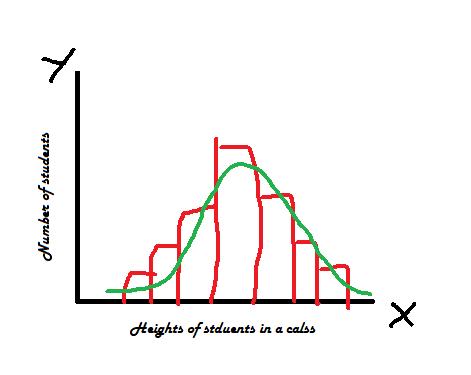
> Frequency distribution of student heights (drawing: author)

那是頻率分布。 但是還有另一種分布-更好地稱為分散-可以顯示變量相對于其中心趨勢如何分散/分布。

色散的經典表示是箱線圖。

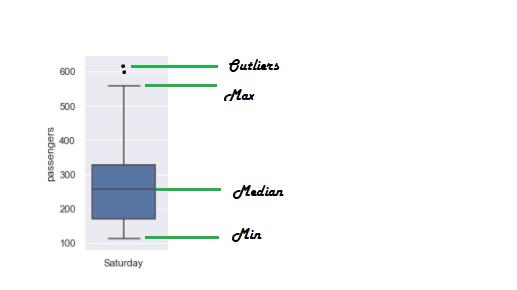
> Decomposition of box plot to show the dispersion of values of a variable

上面的箱線圖表示多年以來周六航空乘客數量的分布。 這個單一的圖顯示了太多的信息-周六的平均乘客數/中位數，最小和最大乘客數，異常值等等!

2)關系

樹木隨著年齡的增長變得越來越高。 那是身高和年齡這兩個變量之間的關系。

身高=(年齡)

在另一個示例中，房屋價格取決于床位數，浴室數量，位置，平方英尺等。這是一個因變量與許多解釋變量之間的關系。

價格=的(床，浴室，位置，面積)

如果僅將數據集視為數字，則無法識別這些關系。 但是實際上，借助良好的可視化，您可以無需進行復雜的統計分析。

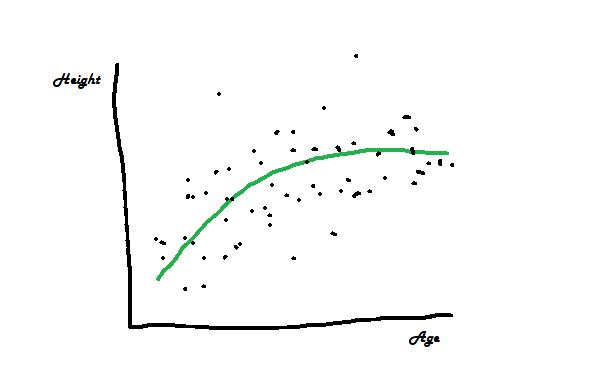
> Relationship between age and height of a class of students

3)比較

數據可視化的第三個基石是比較。 這種視覺材料將數據集中的多個變量或單個變量內的多個類別進行比較。

我們來看看以下兩個視覺效果：

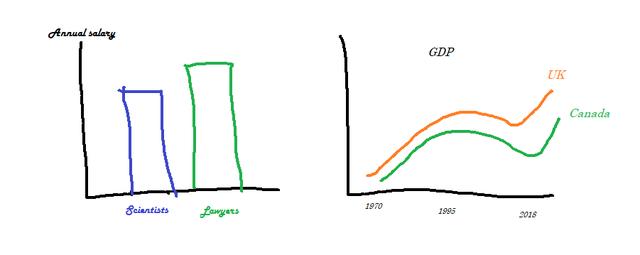
> Visuals to show comparisons

左圖比較條形圖上兩組觀察值(科學家與律師)之間的變量(工資)。 右側面板也是一個比較圖-在這種情況下，是比較兩個組(英國和加拿大)之間但沿時間維度的變量(GDP)。

4)組成

您聽說過堆積條形圖嗎? 但我確定您知道餅圖是什么。

這些圖表的目的是以絕對數和標準化形式(例如百分比)顯示一個或多個變量的組成。

構成圖是當今一些有限的用例的老式可視化技術(您是否真的需要餅圖來顯示黃色10%和紅色15%的組成?)。 但是，有時他們可以以視覺上的審美和熟悉的老式方式呈現信息。

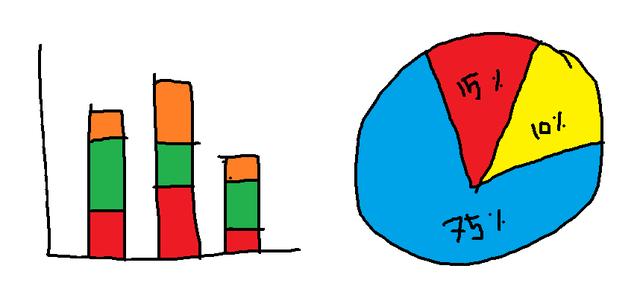
> Composition plots: Stacked bar chart (left) and pie chart (right)

最后的話

本文的目的是討論數據可視化的四個基石：分布，關系，比較和組合。 在學習可視化工具和技術之前，重要的是要了解可視化的目的和要傳達的信息。 在以后的文章中，我將用python和R編程語言寫一些特定的工具，包括matplotlib，seabon和ggplot2。 敬請關注!