5種用于預測銷售的機器學習技術
預測銷售是機器學習(ML)的常見且必不可少的用途。預測銷售可用于確定基準并確定新計劃的增量影響,根據預期需求規劃資源以及規劃未來預算。在本文中,我將展示如何實現5種不同的ML模型來預測銷售。
初期準備
首先我們先加載數據并將其轉換為一個結構,然后將其用于每個模型。以原始格式,每一行數據代表十個商店中一天的銷售額。我們的目標是預測月度銷售額,因此我們將首先將所有商店和天數合并為月度總銷售額。
- def load_data():
- return pd.read_csv('D:\Jupyter\dataset\demand-forecasting-kernels-only/train.csv')
- def monthly_sales(data):
- monthly_data = data.copy()
- monthly_datamonthly_data.date = monthly_data.date.apply(lambda x: str(x)[:-3])
- monthly_datamonthly_data = monthly_data.groupby('date')['sales'].sum().reset_index()
- monthly_data.date = pd.to_datetime(monthly_data.date)
- return monthly_data
- monthly_df = monthly_sales(sales_data)
- monthly_df.head()
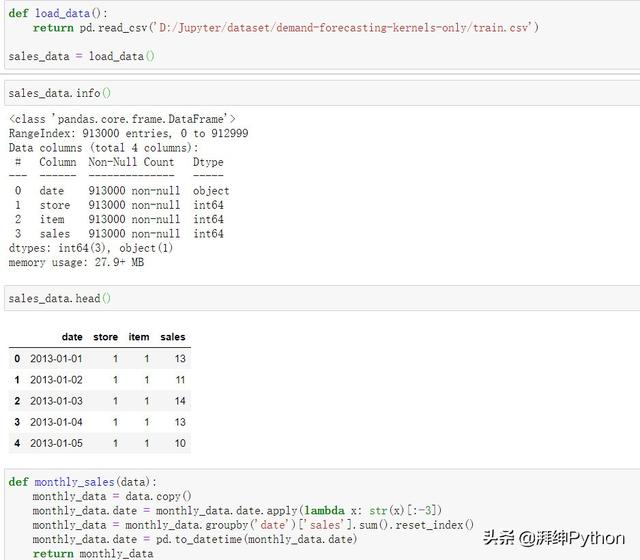
在我們的新數據框中,每一行現在代表所有商店在給定月份的總銷售額。
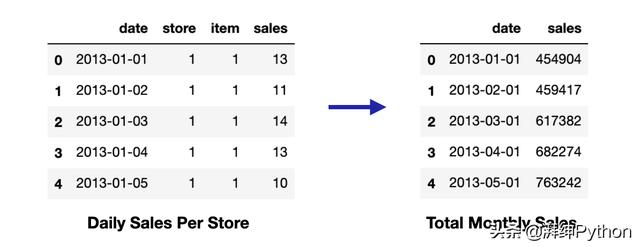
如果我們繪制隨時間變化的每月總銷售量,我們會看到平均每月銷售量隨時間增加,這意味著我們的數據不是固定的。為了使其平穩,我們將計算每月銷售額之間的差異,并將其作為新列添加到我們的數據框中。
- def get_diff(data):
- data['sales_diff'] = data.sales.diff()
- datadata = data.dropna()
- data.to_csv('D:/Jupyter/dataset/demand-forecasting-kernels-only/stationary_df.csv')
- return data
- stationary_df = get_diff(monthly_df)
下面是差異轉換前后數據外觀的直觀表示:
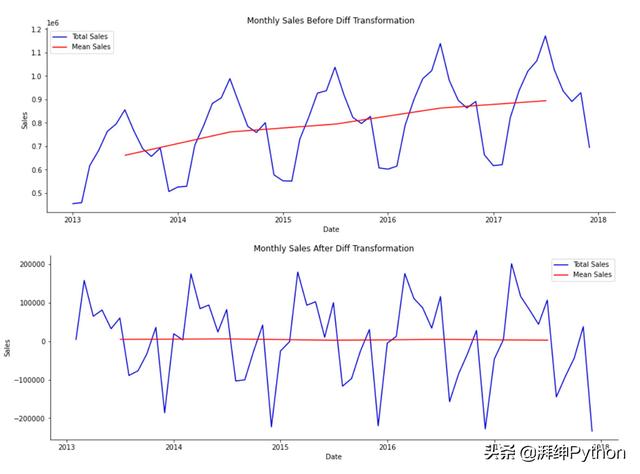
比較差異前后的平穩性
現在,我們的數據代表了每月的銷售額,并且已經將其轉換為固定值,接下來我們將為不同的模型類型設置數據。為此,我們將定義兩種不同的結構:一種將用于ARIMA建模,另一種將用于其余的模型。
對于我們的Arima模型,我們只需要一個日期時間索引和因變量(銷售額差異)列。
- def generate_arima_data(data):
- dt_data = data.set_index('date').drop('sales', axis=1)
- dt_data.dropna(axis=0)
- dt_data.to_csv('D:/Jupyter/dataset/demand-forecasting-kernels-only/arima_df.csv')
- return dt_data
- arima_datetime = generate_arima_data(stationary_df)
對于其他模型,我們將創建一個新的數據框,其中每個特征代表上個月的銷售額。為了確定在我們的特征集中包含多少個月,我們將觀察自相關和部分自相關圖,并在ARIMA建模中使用選擇滯后時間的規則。這樣,我們就可以為我們的ARIMA和回歸模型保持一致的回顧周期。
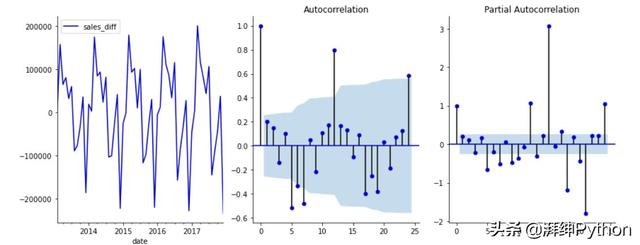
自相關和局部自相關圖
基于上述情況,我們將選擇回溯期為12個月。因此,我們將生成一個包含13列的數據框,12個月每個月為1列,而我們的因變量即銷售額差異列為第1列。
- def generate_supervised(data):
- supervised_df = data.copy()
- #create column for each lag
- for i in range(1,13):
- col_name = 'lag_' + str(i)
- supervised_df[col_name] = supervised_df['sales_diff'].shift(i)
- #drop null values
- supervised_dfsupervised_df = supervised_df.dropna().reset_index(drop=True)
- supervised_df.to_csv('D:/Jupyter/dataset/demand-forecasting-kernels-only/model_df.csv', index=False)
- return supervised_df
- model_df = generate_supervised(stationary_df)
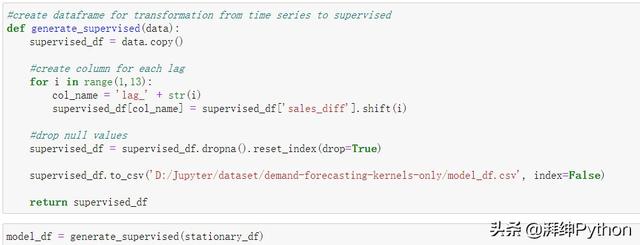
現在我們有兩個獨立的數據結構,一個是Arima結構,它包含一個datetime索引,另一個是監督結構,它包含滯后時間特征。
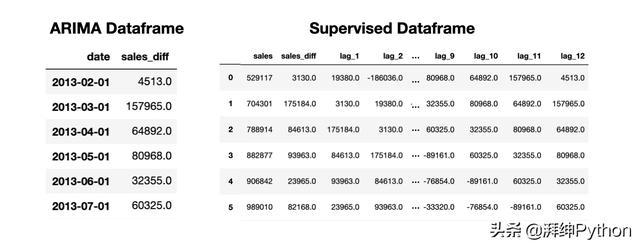
ARIMA和受監督的數據框用于銷售預測
建模
為了創建和評估所有的模型,我們使用了一系列執行以下函數的輔助函數。
- 訓練、測試、拆分:我們將數據分開,使過去的12個月成為測試集的一部分,其余數據用于訓練我們的模型
- 縮放數據:使用最小-最大縮放器,我們將縮放數據,以便所有變量都在-1到1的范圍內
- 反向縮放:運行模型后,我們將使用此輔助函數來反轉步驟2的縮放
- 創建一個預測數據框:生成一個數據框,其中包括在測試集中捕獲的實際銷售額和模型的預測結果,以便我們能夠量化我們的成功
- 對模型評分:這個輔助函數將保存我們預測的均方根誤差(RMSE)和均值絕對誤差(MAE),以比較五個模型的性能
1. 回歸模型:線性回歸,隨機森林回歸,XGBoost
對于我們的回歸模型,我們可以使用scikit-learn庫的fit-predict結構。因此,我們可以建立一個基礎建模結構,我們將針對每個模型進行調用。下面的函數調用上面概述的許多輔助函數來拆分數據,運行模型并輸出RMSE和MAE分數。
- def regressive_model(train_data, test_data, model, model_name):
- # Call helper functions to create X & y and scale data
- X_train, y_train, X_test, y_test, scaler_object =
- scale_data(train_data, test_data)
- # Run regression model
- mod = model
- mod.fit(X_train, y_train)
- predictions = mod.predict(X_test)
- # Call helper functions to undo scaling & create prediction df
- original_df = pd.read_csv('D:/Jupyter/dataset/demand-forecasting-kernels-only/train.csv')
- unscaled = undo_scaling(predictions, X_test, scaler_object)
- unscaled_df = predict_df(unscaled, original_df)
- # Call helper functions to print scores and plot results
- get_scores(unscaled_df, original_df, model_name)
- plot_results(unscaled_df, original_df, model_name)
- # Separate data into train and test sets
- train, test = tts(model_df)
- # Call model frame work for linear regression
- regressive_model(train, test, LinearRegression(),'LinearRegression')
- # Call model frame work for random forest regressor
- regressive_model(train, test,
- RandomForestRegressor(n_estimators=100,
- max_depth=20),
- 'RandomForest')
- # Call model frame work for XGBoost
- regressive_model(train, test, XGBRegressor(n_estimators=100,
- learning_rate=0.2),
- 'XGBoost')
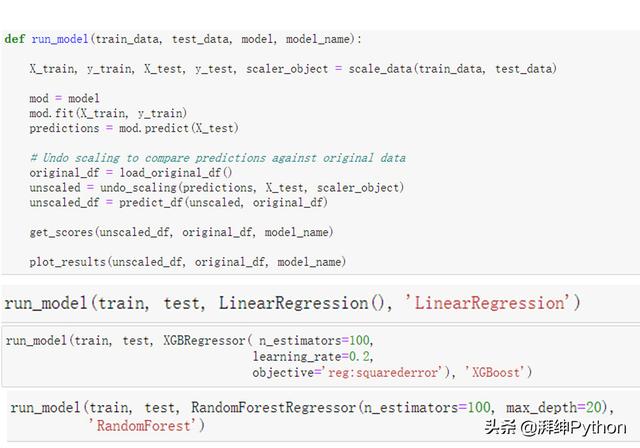
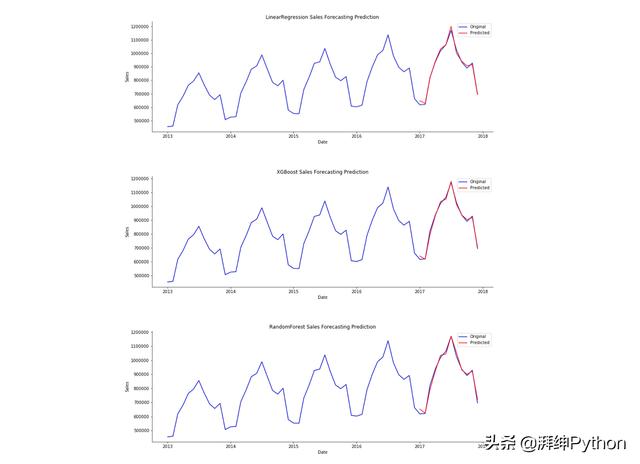
下面的輸出顯示了每個回歸模型的預測(紅色)覆蓋在實際銷售(藍色)之上。雖然結果看起來很相似,但細微的差別相當于幾千美元的銷售額,我們將在下面的比較部分中看到。
2. 長短期記憶(LSTM)
LSTM是一種遞歸神經網絡,對于使用順序數據進行預測特別有用。為此,我們將使用非常簡單的LSTM。為了提高準確性,可以添加周期性特征和附加模型復雜性。
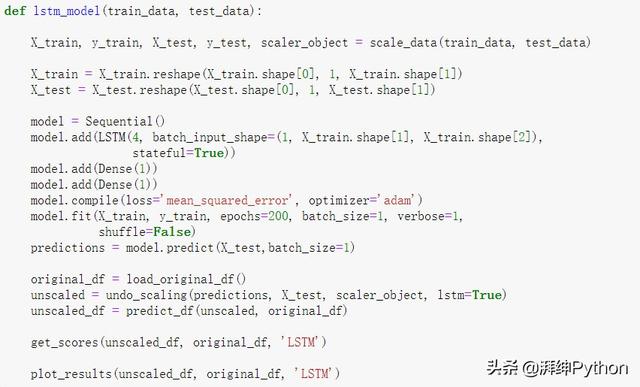
- def lstm_model(train_data, test_data):
- X_train, y_train, X_test, y_test, scaler_object = scale_data(train_data, test_data)
- X_trainX_train = X_train.reshape(X_train.shape[0], 1, X_train.shape[1])
- X_testX_test = X_test.reshape(X_test.shape[0], 1, X_test.shape[1])
- model = Sequential()
- model.add(LSTM(4, batch_input_shape=(1, X_train.shape[1], X_train.shape[2]),
- stateful=True))
- model.add(Dense(1))
- model.add(Dense(1))
- model.compile(loss='mean_squared_error', optimizer='adam')
- model.fit(X_train, y_train, epochs=200, batch_size=1, verbose=1,
- shuffle=False)
- predictions = model.predict(X_test,batch_size=1)
- original_df = load_original_df()
- unscaled = undo_scaling(predictions, X_test, scaler_object, lstm=True)
- unscaled_df = predict_df(unscaled, original_df)
- get_scores(unscaled_df, original_df, 'LSTM')
- plot_results(unscaled_df, original_df, 'LSTM')
生成的圖看起來與上面的三個回歸圖相似,因此我們將繼續比較結果,直到我們看到下面的誤差為止。
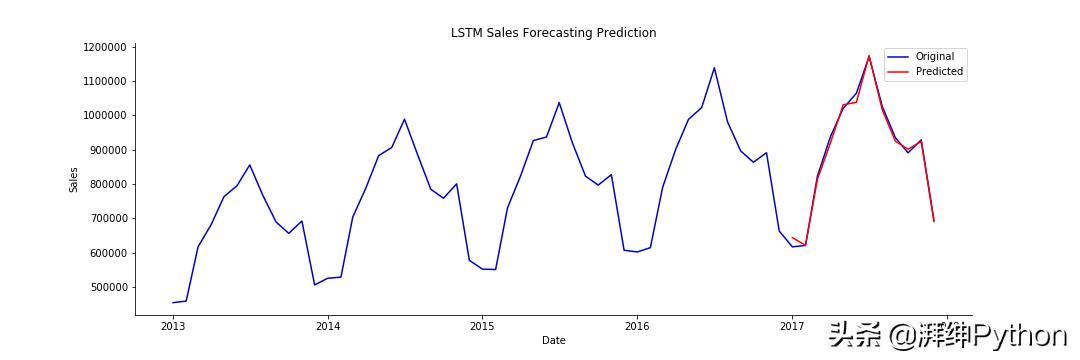
LSTM模型預測與實際銷售額
3. ARIMA
ARIMA模型看起來與上面的模型略有不同。我們使用statsmodels SARIMAX軟件包來訓練模型并生成動態預測。SARIMA模型分為幾個部分。
- AR:表示為p,是自回歸模型
- I:用d表示,是微分項
- MA:表示為q,是移動平均模型
- S:使我們能夠添加周期性成分
在下面的代碼中,我們定義我們的模型,然后對數據的最后12個月進行動態預測。對于標準的非動態預測,下個月的預測是使用前幾個月的實際銷售額進行的。相反,對于動態預測,使用前幾個月的預測銷售額進行下個月的預測。
- def lstm_model(train_data, test_data):
- X_train, y_train, X_test, y_test, scaler_object = scale_data(train_data, test_data)
- X_trainX_train = X_train.reshape(X_train.shape[0], 1, X_train.shape[1])
- X_testX_test = X_test.reshape(X_test.shape[0], 1, X_test.shape[1])
- model = Sequential()
- model.add(LSTM(4, batch_input_shape=(1, X_train.shape[1], X_train.shape[2]),
- stateful=True))
- model.add(Dense(1))
- model.add(Dense(1))
- model.compile(loss='mean_squared_error', optimizer='adam')
- model.fit(X_train, y_train, epochs=200, batch_size=1, verbose=1,
- shuffle=False)
- predictions = model.predict(X_test,batch_size=1)
- original_df = load_original_df()
- unscaled = undo_scaling(predictions, X_test, scaler_object, lstm=True)
- unscaled_df = predict_df(unscaled, original_df)
- get_scores(unscaled_df, original_df, 'LSTM')
- plot_results(unscaled_df, original_df, 'LSTM')
同樣,結果看起來還不錯。我們將在下面進一步進行挖掘。
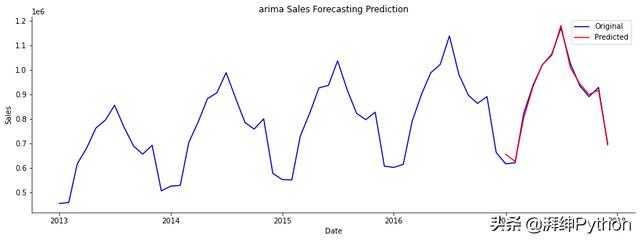
ARIMA模型預測與實際銷售額
比較模型
為了比較模型性能,我們將查看均方根誤差(RMSE)和均值絕對誤差(MAE)。這些指標通常都用于比較模型性能,但是它們的直覺和數學含義略有不同。
- MAE:均值絕對誤差告訴我們,我們的預測與真實值之間的距離。在這種情況下,所有誤差的權重都相同。
- RMSE:我們通過取所有平方誤差之和的平方根來計算RMSE。當我們平方時,較大的誤差對整體誤差有較大的影響,而較小的誤差對整體誤差沒有太大的影響。
從上面的輔助函數中,我們使用get_scores計算每個模型的RMSE和MAE分數。這些分數保存在字典中并保存起來。為了進行比較,我們將把字典轉換成Pandas數據框并繪制結果。
- def create_results_df():
- results_dict = pickle.load(open("model_scores.p", "rb"))
- results_dict.update(pickle.load(open("arima_model_scores.p", "rb")))
- restults_df = pd.DataFrame.from_dict(results_dict, orient='index',
- columns=['RMSE', 'MAE','R2'])
- restults_dfrestults_df = restults_df.sort_values(by='RMSE', ascending=False).reset_index()
- return restults_df
- results = create_results_df()
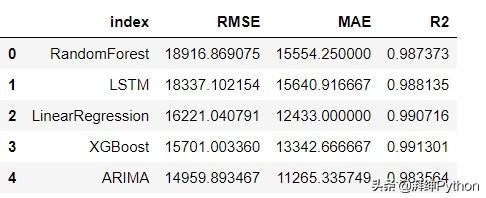
這為我們提供了以下數據框。
我們可以看到,盡管我們的模型輸出在上圖中看起來相似,但它們的準確度確實有所不同。下面是可以幫助我們看到差異的視覺效果。
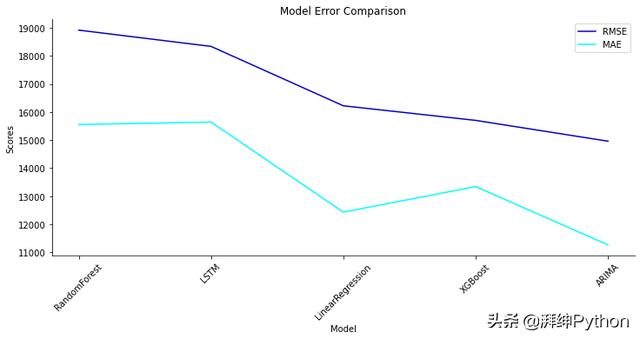
比較模型性能
結論
我們看到的是,總體而言,XGBoost模型具有最佳性能,緊隨其后的是ARIMA和LSTM模型。需要注意的是,以上所有模型都是以其最基本的形式衍生的,以演示如何將其用于銷售預測。僅對模型進行了微調,以最大程度地減少復雜性。例如,LSTM可以具有許多其他節點和層以提高性能。
要確定哪種模型適合您的用例,應考慮以下內容:
- 模型復雜度與可解釋性的程度。
- 可以調整模型,并可以對函數進行設計以包括周期性信息,節假日,周末等。
- 了解如何使用結果以及如何輸入數據來更新模型。
- 使用交叉驗證或類似技術來調整模型,以避免數據過度擬合。