學好數理化，走遍天下都不怕!這句話我們從小就聽，放到今天似乎依然行得通。達芬奇說：“數學是一切科學的基礎”，數學與代碼之間也有著千絲萬縷的聯系。

[[320686]]

似乎任何熱衷于機器學習、數據科學的人都相信，總有一天，他們將研究透徹python庫，暢享里面的數學知識。大量論文集將展現在你面前，詳細說明其原理。對核心數學的理解越深入，你就越可能獲得靈感，創造新方法。

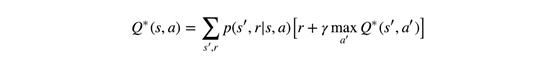
對于多年來鉆研數學或從事機器數學學習的人來說，將上面這個方程式詳細地解析為含義和代碼并不難。但是對大部分普通人來說，無異于看天書。古代數學家似乎都喜歡用有趣的外觀符號來表述直觀的方法，但卻使方程和變量復雜化了。

實際上，代碼不僅可以編寫程序，還可以讓這些復雜的語言再次變得直觀起來。加深對數學理解的最好方法就是編寫代碼段來描述方程式，這會讓理解變得簡單起來。

看過下面這些例子，相信你也會有這樣的感覺。

求和與乘積

求和符號是迭代數學中最有用和最常用的符號之一。盡管設計復雜，但運算是相當簡單且有用。

x = [1,2, 3, 4, 5] 
result = 0for i in range(5): 
    result += x[i]Output of print(result)-> 15 

如上所示，此符號代表從頂部的數字開始的for循環，頂端數字為最大值。在底部設置的變量將成為索引變量，并且每個循環的所有結果都將添加到總值中。

上面這個符號被稱為乘積運算符，跟求和符號運算方式相似，但不會相加每個結果，而是將它們相乘。

x = [1,2, 3, 4, 5] 
result = 1for i in range(5): 
    result *= x[i]Output of print(result)-> 120 

條件括號

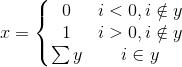
條件括號用于在特定條件下轉換方程的等式。對于碼農，常見的“ if”語句就是這樣。把它用代碼表述是這樣的：

i = 3 
y = [-2, 3, 4, 1] 
result = 0if i in y: 
result = sum(y) 
elif i > 0: 
result = 1 
else: 
result = 0print(result) -> 6 

如上所示，每一行括號中的正確表示法指定了每條路徑應執行的操作。我也將多余的“包含”符號添加到每個條件中，以加強理解。我們檢查了i值是否在y列表中。確認過后，返回數組的總和。如果i值不在數組中，將基于該值返回0或1。

階乘

階乘用“!”表示，幾乎所有計算器上都有此符號。這個符號會好理解一些，不過代碼會帶你進一步了解它的原理。

5!將表示為：

result =1 
for i in range(1,5): 
result *= i 
Output of print(result) -> 120 

逐點操作和笛卡爾矩陣乘法

再來看一下數據科學家們經常使用的語言庫(矩陣乘法)如何完成操作。逐點操作很容易理解，簡寫為：

請注意，該操作首先要求每個矩陣必須具有這樣的模型(即#行 =&#列=)

其代碼如下所示：

y =[[2,1],[4,3]] 
z = [[1,2],[3,4]] 
x = [[0,0],[0,0]]for i in range(len(y)): 
for j in range(len(y[0])): 
        x[i][j] = y[i][j] *z[i][j]print(x) -> [[2, 2], [12, 12]] 

最后，讓我們看一下機器學習中最常用的典型矩陣乘法。用復雜的術語來說，此運算為每個主要行與每個次要列的點積。

具體操作是：假設[#行，#列]→矩陣ixj要求#列(i)== #行(j)→最終輸出的模型為[#行(i)， #列(j)]

看起來似乎很難理解，圖片能幫助你直觀了解這些操作。

該方程的代碼如下(使用numpy點法)：

y =[[1,2],[3,4]] 
z = [[2], [1]] 
# x has shape [2, 1] 
x = [[0], [0]]for i in range(len(y)) 
for j in range(len(z): 
        x[i][j] = np.dot(y[i], z[:, j]) 
print(x) -> [[4], 
             [10]] 

看完這幾個簡單的示例，是不是有種撥開迷霧見光明的感覺!

用簡單的代碼學習數學，你會大有收獲的。