Jeremy Howardf 老師曾在生成對抗網絡(GAN)課程中說過：「……本質上，GAN 就是另一種損失函數。」

本文將在適合的相關背景下討論上面的觀點，并向大家闡述 GAN 這種「學得」(learned)損失函數的簡潔優美之處。

首先，我們先介紹相關背景知識：

從函數逼近的角度看神經網絡

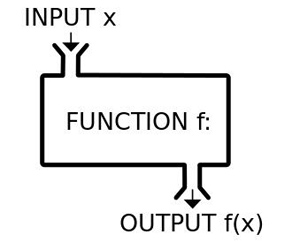
在數學中，我們可以把函數當做機器，往機器中輸入一或多個數字，它會相應地生成一或多個數字。

將函數比作「機器」或「黑箱」。(圖源：https://www.wikiwand.com/en/Function_%28mathematics%29)

如果我們能夠用數學公式表示函數，這很好。可如果大家不能或尚未想明白如何將想要的函數寫成一系列加減乘除(譬如分辨輸入是貓圖像還是狗圖像的函數)又該如何呢?

如果無法用公式表達，那我們能否至少逼近函數呢?

神經網絡來拯救我們了。萬能逼近定理表明，一個具有充足隱藏單元且足夠大的神經網絡可以計算「任何函數」。

具備 4 個隱藏單元的簡單神經網絡逼近塔型函數。

(圖源：http://neuralnetworksanddeeplearning.com/chap4.html)

神經網絡的顯式損失函數

掌握神經網絡后，我們就可以構建一個神經網絡以逐步逼近上文所述的貓狗分類函數，而無需顯式地表達該分類函數。

為了獲得更好的函數逼近能力，神經網絡首先需要知道其當前性能有多差。計算神經網絡誤差的方式被稱為損失函數。

目前已經有很多損失函數，對于損失函數的選擇依賴于具體任務。然而，所有損失函數具有一個共同特性──它必須能以精確的數學表達式表示損失函數。

• L1 損失(絕對誤差)：用于回歸任務
• L2 損失(平方誤差)：與 L1 類似，但對于異常值更加敏感
• 交叉熵誤差：通常用于分類任務
• Dice 損失 (IoU) ：用于分割任務
• KL 散度：用于衡量兩種分布之間的差異
• ……

關于神經網絡逼近特性的好壞，損失函數承擔著十分重要的作用。對于神經網絡構建人員來說，針對具體任務去理解和選擇恰當的損失函數是最重要的技能。

目前，設計更好的損失函數也是活躍度極高的研究領域。譬如，論文《Focal Loss for Dense Object Detection》介紹了一種名為「Focal loss」的新型損失函數，用于解決單階段目標檢測模型的不平衡性。

顯式損失函數的局限

前文所述的損失函數在分類、回歸及圖像分割等任務中的表現相當不錯，而針對輸出具有多模態分布的情況，則效果堪憂。

以黑白圖片著色任務為例。

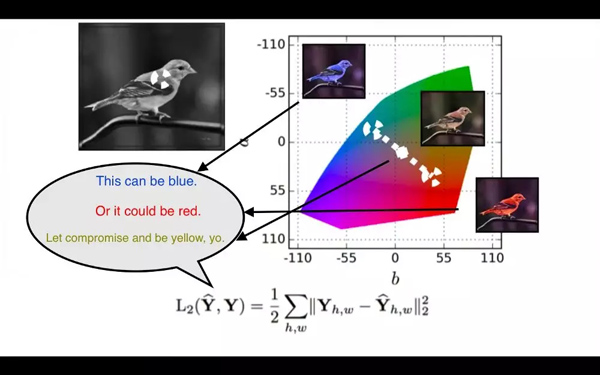
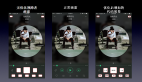
L2 損失函數的思考過程。(圖源：https://youtu.be/8881p8p3Guk?t=2971)

• 輸入是黑白色的鳥，真實圖像是相同的藍色的鳥。
• 采用 L2 損失函數計算模型的輸出顏色與真實圖像的像素級差異。
• 接下來，輸入是與剛才實驗相似的一只黑白色的鳥;真實圖像是一只相同的紅色的鳥。
• L2 損失函數試圖最小化模型的輸出顏色與紅色的差異。
• 基于 L2 損失函數的反饋，模型已學習出一只相似的鳥，但模型應該輸出一種與紅色及藍色都接近的顏色。模型會怎么做?
• 模型會輸出一種黃色的鳥，這是最小化紅色與藍色距離的最安全選擇，即便模型在訓練過程中從未觀察到一只黃色的鳥。
• 由于實際上沒有黃色鳥，所以你知道模型不夠逼真。

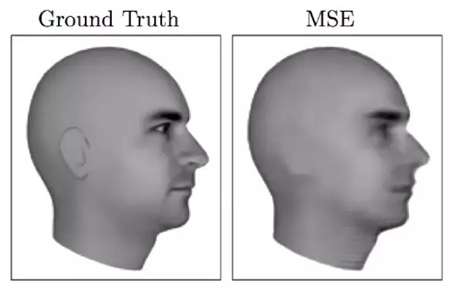
基于均方差預測的下一幀圖像非常模糊。(圖源：https://arxiv.org/pdf/1605.08104.pdf)

這種均化效應在許多實例中會導致非常糟糕的結果。以預測視頻下一幀任務為例，下一幀的可能性非常多，你想要的是能輸出「其中某一幀」的模型。但是，如果采用 L2 或 L1 訓練模型，模型將平均所有可能結果，生成一張十分模糊的均化圖像。

GAN 作為新的損失函數

首先，你并不知道復雜函數的精確數學表達式(比如函數的輸入是一組數字，輸出是一張狗狗的逼真圖像)，所以你使用神經網絡逼近此函數。

神經網絡需要損失函數告知它目前性能的好壞，但沒有任何顯式損失函數能夠很好的完成此項工作。

嗯，要是有一種既無需顯式數學表達式，又能夠直接逼近神經網絡損失函數的方法，該多好。譬如神經網絡?

所以，如果我們用神經網絡模型替代顯式損失函數，將會怎樣?恭喜，你發現了 GAN。

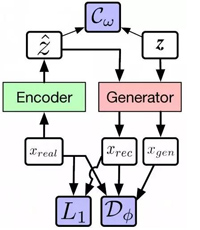
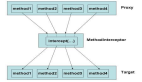
通過下面的 GAN 架構和 Alpha-GAN 架構，你能觀察地更清晰。如圖，白色框代表輸入，粉色框和綠色框代表你想構建的網絡，藍色框代表損失函數。

GAN 架構

Alpha-GAN 架構

在原版 GAN 中僅有一種損失函數——判別器網絡 D，其自身就是另一種神經網絡。

而在 Alpha-GAN 中，模型有 3 種損失函數：輸入數據的判別器 D、用于已編碼潛變量的潛碼判別器 C，以及傳統像素級 L1 損失函數。其中，D 和 C 并不是顯式損失函數，而只是其近似──神經網絡。

梯度

如果將判別器(同樣也是神經網絡)作為損失函數來訓練生成器網絡(與 Alpha-GAN 的編碼器)，那么用什么損失函數來訓練判別器呢?

判別器的任務是區分真實數據分布與生成數據分布。用監督方式訓練判別器時，標簽可隨意使用，所以采用二元交叉熵等顯式損失函數訓練判別器就很簡單。

但由于判別器是生成器的損失函數，這代表判別器的二元交叉熵損失函數的累積梯度同樣會被用于更新生成器網絡。

觀察 GAN 中的梯度變化，就非常容易發現改變其軌跡的新思路。如果顯式損失函數的梯度無法在兩個神經網絡間(判別器和生成器)回流，卻可以在三個神經網絡間回流，那么它能被應用在何處?如果梯度無法通過傳統損失函數回流，卻可在這些神經網絡之間直接來回呢?從基本原理出發，我們很容易發現未被探索的路徑以及未被解答的問題。

結論

通過傳統損失函數與神經網絡的集成，GAN 使將神經網絡作為損失函數來訓練另一神經網絡成為可能。兩個神經網絡間的巧妙交互使得深度神經網絡能夠解決一些先前無法完成的任務(如生成逼真圖像)。

將 GAN 本質上視為一種學得的損失函數，我希望這篇文章能夠幫助大家理解 GAN 的簡潔和力量。

原文鏈接：https://medium.com/vitalify-asia/gans-as-a-loss-function-72d994dde4fb

【本文是51CTO專欄機構“機器之心”的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】

戳這里，看該作者更多好文