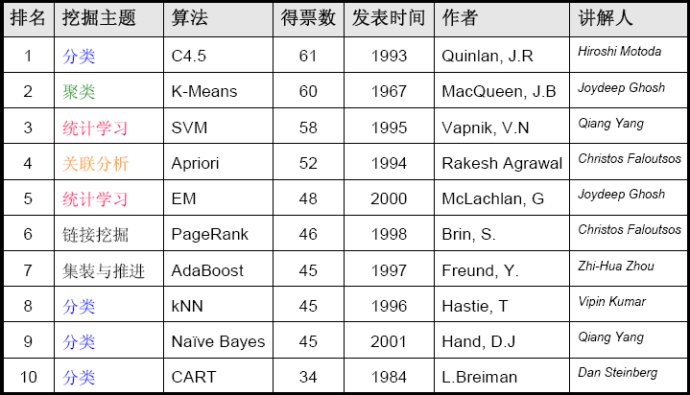
數據挖掘十大經典算法如下：

簡介

C4.5是決策樹算法的一種。決策樹算法作為一種分類算法，目標就是將具有p維特征的n個樣本分到c個類別中去。常見的決策樹算法有ID3,C4.5,CART。

基本思想

下面以一個例子來詳細說明C4.5的基本思想

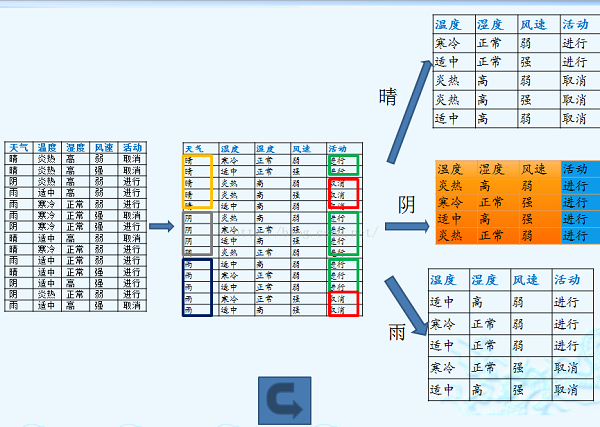
上述數據集有四個屬性，屬性集合A={ 天氣，溫度，濕度，風速}， 類別標簽有兩個，類別集合L={進行，取消}。

1. 計算類別信息熵

類別信息熵表示的是所有樣本中各種類別出現的不確定性之和。根據熵的概念，熵越大，不確定性就越大，把事情搞清楚所需要的信息量就越多。

2. 計算每個屬性的信息熵

每個屬性的信息熵相當于一種條件熵。他表示的是在某種屬性的條件下，各種類別出現的不確定性之和。屬性的信息熵越大，表示這個屬性中擁有的樣本類別越不“純”。

3. 計算信息增益

信息增益的 = 熵 - 條件熵，在這里就是 類別信息熵 - 屬性信息熵，它表示的是信息不確定性減少的程度。如果一個屬性的信息增益越大，就表示用這個屬性進行樣本劃分可以更好的減少劃分后樣本的不確定性，當然，選擇該屬性就可以更快更好地完成我們的分類目標。

信息增益就是ID3算法的特征選擇指標。

但是我們假設這樣的情況，每個屬性中每種類別都只有一個樣本，那這樣屬性信息熵就等于零，根據信息增益就無法選擇出有效分類特征。所以，C4.5選擇使用信息增益率對ID3進行改進。

4.計算屬性分裂信息度量

用分裂信息度量來考慮某種屬性進行分裂時分支的數量信息和尺寸信息，我們把這些信息稱為屬性的內在信息(instrisic information)。信息增益率用信息增益 / 內在信息，會導致屬性的重要性隨著內在信息的增大而減小(也就是說，如果這個屬性本身不確定性就很大，那我就越不傾向于選取它)，這樣算是對單純用信息增益有所補償。

5. 計算信息增益率

(下面寫錯了。。應該是IGR = Gain / H )

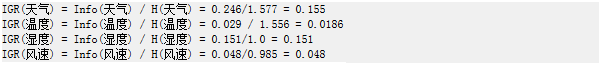
天氣的信息增益率最高，選擇天氣為分裂屬性。發現分裂了之后，天氣是“陰”的條件下，類別是”純“的，所以把它定義為葉子節點，選擇不“純”的結點繼續分裂。

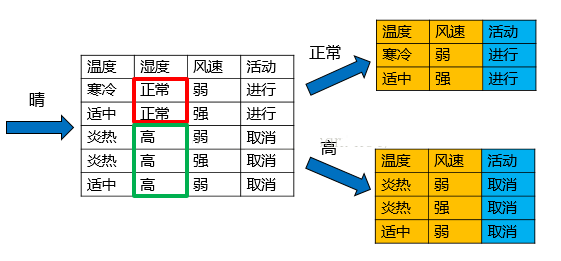
在子結點當中重復過程1~5。

至此，這個數據集上C4.5的計算過程就算完成了，一棵樹也構建出來了。

總結算法流程為：

優缺點

優點

產生的分類規則易于理解，準確率較高。

缺點

在構造樹的過程中，需要對數據集進行多次的順序掃描和排序，因而導致算法的低效。

代碼

代碼已在github上實現，這里也貼出來

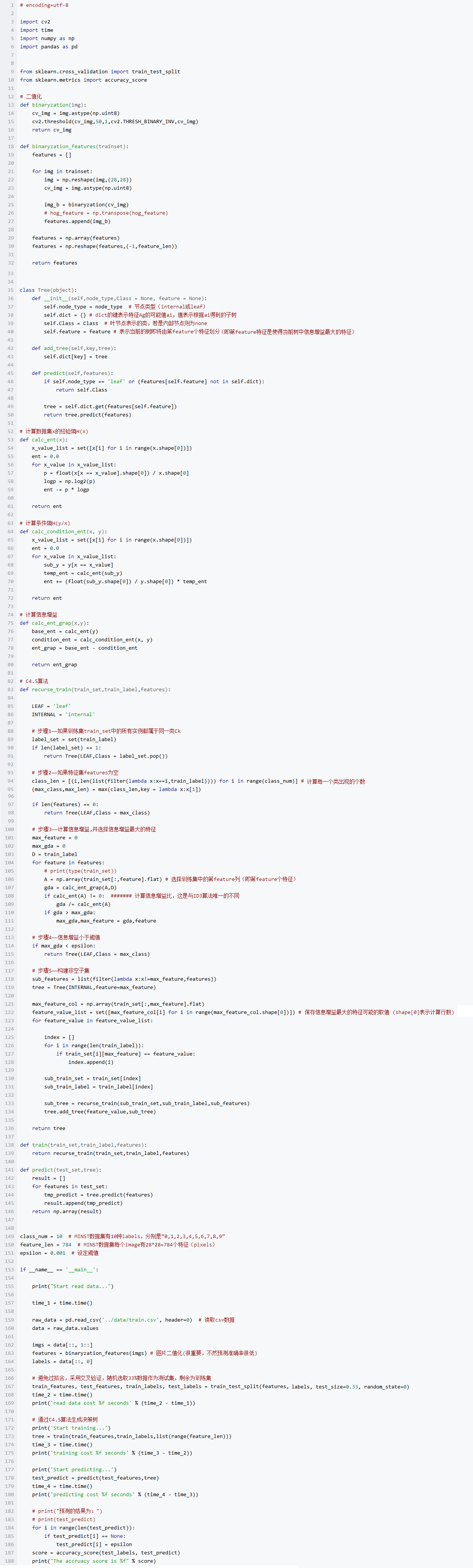
測試數據集為MNIST數據集，獲取地址為train.csv

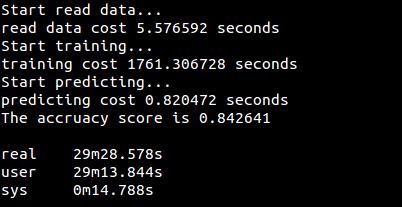
運行結果