大家好，我是Siraj。

讓我們將目光高度聚焦在概率論在機器學習中扮演的角色，通過從頭開始構建一個垃圾郵件分類器。

數(shù)學概念在生活中的應用

生活中充滿了不確定性，我們嘗試一些自己覺得會成功的事情，但我們無法確定，比如今天是否會下雨，或者在眾人注視下跳舞是否合適，亦或是我是否該在這段感情中投入更多。概率論給我們搭建了一個大的框架來進行上述的決策，而通過這么做, 我們能做出更有效的決策。

數(shù)學的一些分支理論方法，能夠在我們有完整信息時幫助我們做出決定，但是概率論能夠訓練我們，在規(guī)律性與不確定性并存時做出決定。就像我們真實的生活，它是用來衡量某事發(fā)生的可能性。

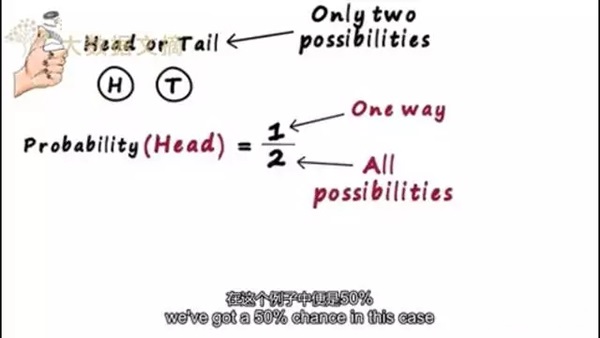
而分析服從一定概率分布的事件規(guī)律這一學科，叫做統(tǒng)計學。一個簡單的例子便是拋硬幣，只會存在兩種結果，即正或者反，我們可以對正面出現(xiàn)的概率進行建模，因為我們知道兩個要素，即事情可能發(fā)生的方式以及總共能出現(xiàn)的結果，在這個例子中便是50%。

就像藍牙的工作頻率一樣，這是一個隨機的變量，它代表著一件我們無法確定的事，無法確定的事并無法像代數(shù)那樣用變量進行表述。相反的，它有一組可能的取值，也稱作樣本空間，以及這組里的每一個取值可能發(fā)生的概率是通過這樣表示的。它們既可以是離散的，只表示一定數(shù)量的值，也可以是連續(xù)的，能夠取到一定范圍內(nèi)的任何值。

假設現(xiàn)在有兩件可能發(fā)生的事情 A和B，比如，我們拋一枚硬幣，以及擲一枚六面的骰子。我們可以用三種方式來衡量它們的可能性，即當硬幣是正面時，骰子是4的概率，這便是條件概率。

我們也可以對兩件事情同時發(fā)生的概率建模，比如說，硬幣落在正面同時骰子落在4的概率是什么，這便是聯(lián)合概率。而如果我們想要知道某種特定結果的概率，比如說，僅僅只是硬幣或者僅僅只是骰子的投擲概率，這種便被稱為邊際概率。

貝葉斯統(tǒng)計

在機器學習中我們做了很多類似的假設，有些時候它們是錯的(一家公司)，現(xiàn)在十分流行使用貝葉斯定理，它構建于條件概率的原理之上。

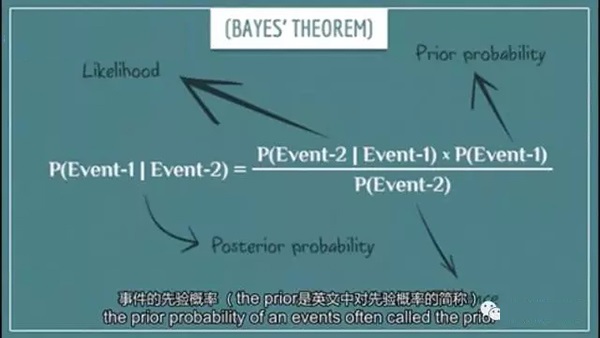
它之所以被稱為定理，是因為我們可以通過邏輯來證明它的真實性。理論中說道，對于兩個事件A和B，如果我們知道在A已知的條件下B發(fā)生的條件概率，以及A事件發(fā)生的概率，我們能計算得到已知B事件的條件下A發(fā)生的條件概率。

換句話來說，已知B的條件下，A發(fā)生的后驗概率，能夠通過下述方法計算得到，即將已知的可能性乘以先驗概率，并將乘積除以已知的概率值，事件的先驗概率 (the prior是英文中對先驗概率的簡稱)，它是利用已有的信息計算得出的概率。

某一天有雨的事前概率可以計算為0.6，在過去的100年里這個日期60%都有雨，我們從一個事前概率入手，現(xiàn)在我們得到了新的信息，從而更準確的重新估計此概率。

如貝葉斯統(tǒng)計學家Lindley所言，掏出槍，當你看到...(此處為2pac Hit'em Up歌詞)，等等...他說的是今天的事后概率就是明天的事前概率，我們可以利用這個定理，根據(jù)新的知識來更新概率。

如果木板斷裂，這個小車而墜毀的概率是多少?木板斷裂的概率為0.3，小車墜毀的概率為0.5。利用貝葉斯定理，墜毀幾率為20%，事故避免啦，那么如何將此應用于機器學習中呢?

有這么一個線性分類器的家族，它們基于貝葉斯定理，被稱為樸素貝葉斯分類器，它們往往表現(xiàn)得非常好，尤其是對于小樣本來說，因此它們要優(yōu)于其他更強大的替代品。

實戰(zhàn)上手垃圾電子郵件的分類

樸素貝葉斯分類器廣泛應用于一系列不同的領域，從診斷疾病，到情緒分析，到我們接下來要做的垃圾電子郵件的分類。

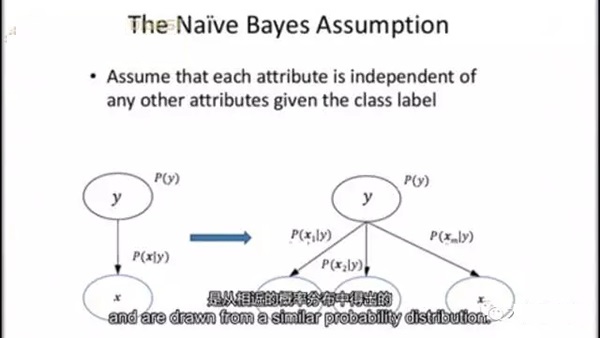
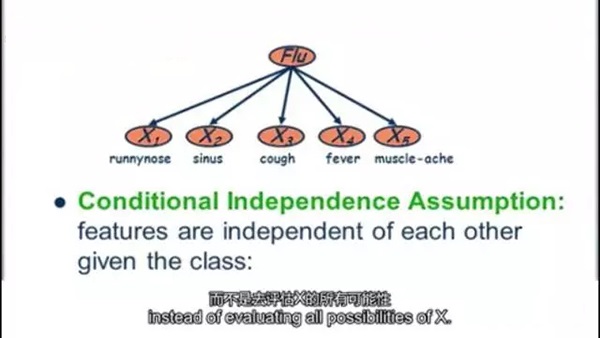
它們對數(shù)據(jù)做了兩個很大的假設，***個假設，樣本是獨立且同分布的，它們是兩兩相互獨立的隨機變量，是從相近的概率分布中得出的;第二個假設，特征的條件獨立性，這意味著樣本的概率，可以從訓練數(shù)據(jù)中直接估計得出，而不是去評估X的所有可能性。因此給定一個N維特征向量，我們可以計算類條件概率，意思是說有多大可能性可以觀測到這個特定模式，假定它屬于類別Y的話，在實踐中，這種假設被違反了相當長的時間，盡管它們的表現(xiàn)還是很不錯的。

***個假設

第二個假設

為了使用樸素貝葉斯做一個預測，我們將計算屬于每個類別中的情況的概率，并使類值達到***，對樸素貝葉斯分類器來說，這種分類數(shù)據(jù)是一個很好的用例。首先我們來加載數(shù)據(jù)文件，它是CSV格式，所以我們可以使用流行的數(shù)據(jù)處理模塊pandas打開文件，并利用其讀取功能將每一行存儲在數(shù)據(jù)框中，每個電子郵件都標記為垃圾或非垃圾郵件。

我們可以將數(shù)據(jù)分割成一個測試我們模型的訓練集，和一個評估其預測能力的測試集，對于我們在貝葉斯定理背景下的垃圾郵件分類問題，我們可以將A設為電子郵件是垃圾郵件的概率。而B設為電子郵件的內(nèi)容，因此如果電子郵件是垃圾郵件的概率，大于它不是垃圾郵件的概率，那么我們將其分類為垃圾郵件，否則我們就不會由于貝葉斯定理在兩種情況下都會導致B的概率作為除數(shù)。

因此可以將其從我們的比較方程中約去，計算A和非A的概率很簡單，它們不過是我們的訓練集中，垃圾郵件和非垃圾郵件的百分比，更為困難的部分是計算，A的條件下B的概率和非A的條件下B的概率，為了做到這個，我們需要“詞袋”模型(BOW)。意思是我們把一段文字作為一組無重復詞群來提取，忽略每個單詞的順序。

對于每個單詞，我們計算出它出現(xiàn)在垃圾郵件中 和非垃圾郵件中的百分比，如果要計算一封完整郵件的另一種條件概率，我們就看郵件中出現(xiàn)的每個單詞的之前的條件概率相乘之后的結果，這個是在分類中進行， 而不是在訓練時。

我們可以構造自己的分類函數(shù)，這類函數(shù)在碰到每封郵件的時候就會啟用，并且使用我們之前定義的方程去對它們進行分類，這個就是全部現(xiàn)在我們能很容易地對新郵件進行分類 把他們分成垃圾或者非垃圾郵件。

如果我們想要分類的郵件中的單詞，不在我們的訓練集里呢?不管怎樣，我們要解決這個極端例子的問題。解決的方法是用一種叫，它可以讓我們將代碼就作為”Alpha“變量輸入，這個意味著每一次我們加1，所以它永遠不會是零，因為如果不是這樣操作的話，他會把某個單詞的概率設定成零 (比如說”警察“)，這樣的話 整個郵件的概率也變成了零，不管這封郵件中出現(xiàn)了多少個其它垃圾性詞組，我們至今都還沒有好的答案。

就是如果我們把模型自己變成隨機會怎么樣，的意思是像結構中的嵌入隨機變量，變分自動編碼器，很棒的一篇論文，我會發(fā)你的，請務必，我們或許還能把我們的模型造得和你一樣變幻莫測，我很多變的，對于我們的模型有沒有什么我們可以改進的地方?

當然啦!我們本可以用一些更有效率的技術，而不是詞袋，并且用egram而不是數(shù)每個單詞，但是朋友們，今天這個視頻已經(jīng)內(nèi)容夠多的了。

總結一下，概率論將有助于我們正式地將生活中的不確定因素用模型建立出來，這簡直太棒啦，貝葉斯定律描述一件事情的概率是基于，之前所有可能和這個事件相關的條件，樸素貝葉斯分類器，將帶有獨立性假設的貝葉斯定律應用于各種特征之中。

來源：https://www.youtube.com/watch?v=PrkiRVcrxOs&t=6s

【本文是51CTO專欄機構大數(shù)據(jù)文摘的原創(chuàng)譯文，微信公眾號“大數(shù)據(jù)文摘（ id: BigDataDigest）”】

戳這里，看該作者更多好文