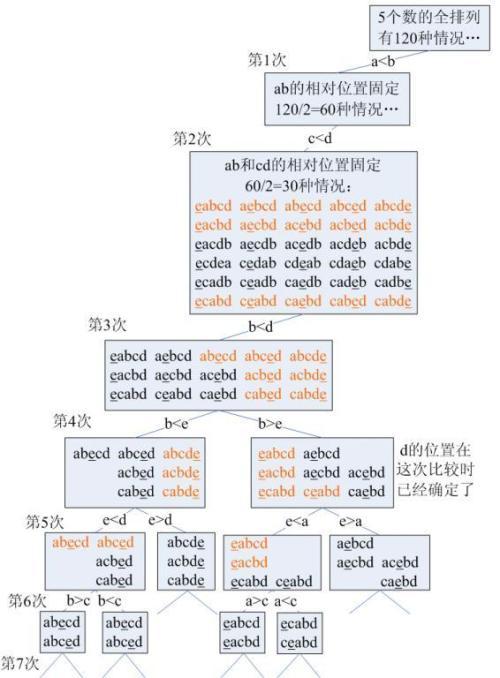
為什么說任何基于比較的算法將5個元素排序都需要7次?
排序算法對結(jié)果的唯一要求就是操作數(shù)滿足全序關(guān)系:
- 如果 a≤b 并且 b≤c 那么 a≤c(傳遞性)。
- 對于 a 或 b,要不 a≤b,要不 b≤a(完全性)。
這個問題可以用信息論來回答。
我從 1 到 5 中挑一個數(shù)字出來讓你來猜,每回合你都可以問我一個問題,我的回答“是”或“不是”(1 或 0),那么你至少需要幾個回合才能保證猜出這個數(shù)字?
比較符合這個游戲精神的玩法是從自己的幸運數(shù)字(比如我的是7)開始猜起,一個一個地問我“是不是X?”, 可能你的運氣足夠好,一個回合就能夠猜對,但是在最壞的情況下可能就需要5個回合,所以你的答案應(yīng)該是“至少需要5個回合” (事實上你至少只需要一次就“有可能”猜出來,但為了“保證能”猜出來,你只好委曲求全地說 5), 換句話說這種猜法的最優(yōu)下界是 5。 (平均性能是 1×1/5+2×1/5+…+5×1/5=(1+…+5)/5 = 3)
但因為你會二分,所以會這樣問“是不是比3大?”……而且無論我挑出的數(shù)字是幾,都只用3個回合。 二分顯然是一種更佳的策略,那么它好在什么地方呢? 用信息論理解: 最大的熵。
英文版維基百科詞條有個大致的解釋:Comparison_sort, 最少次數(shù)為 log(5!) = 6.91,取整的話,就是 7。
決策樹如下:
如果我們用歸并排序的話,比較次數(shù)是O(nlogn),因為歸并排序是 全局最優(yōu)解,但是在局部,歸并并不都保證是最優(yōu)的。
附一張快速排序的 gif 圖: