數據結構中二叉樹的基本操作
二叉樹的基本操作,可能包括:
創建,遍歷,轉化,復制,刪除等。
遍歷:前中后三種順序的遍歷,已經是各數據結構與算法教程的最基礎內容,在此不重復。
創建:大多數據結構教程當中的二叉樹創建程序,都是采用的遞歸方式,遞歸方式創建的二叉樹與遍歷的過程相似,所創建的二叉樹,也是采用左右子節點方式,后續進行遍歷操作十分方便。
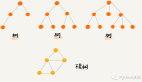
轉化:直覺上,最簡單的二叉樹存儲方式其實是如下圖的數組:

*此圖出自某高校數據結構ppt,但實在難以查證是哪個學校,無法直接感謝,請諒解。
首先,提供個滿二叉樹大小的數組,然后其中數值按完全二叉樹存儲。
顯然,此種順序存儲方法:第i號(這里編號指對應的完全二叉樹的位序)結點的左右孩子一定保存在第2i及2i+1號單元中。
故此,為兼顧存儲的直觀與遍歷等操作的方便,從順序數組向左右子節點存儲方式的轉化也就十分重要。
1-轉化方法
分為幾個步驟:
(1)準備原始數組
(2)分析數組中的有效值,對應二叉樹節點非空;
(3)創建二叉樹節點;
(4)計算除最后一層子節點外,構造節點間父子關系時的循環次數;
(5)構造二叉樹節點間的父子關系;
(6)確實二叉樹根節點;
主要代碼:
(1)準備原始數組
- //原始數組
- int intBiTreeInit[ARR_COUNT];
- //初始化原始數組至無效值
- for(int i=0;i<=ARR_COUNT-1;i++)
- intBiTreeInit[i]=NVALUE;
- //本if條件確保ARR_COUNT是否是的乘方-1
- if(0==(ARR_COUNT & (ARR_COUNT+1)))
- {
- for(int i=0;i<=ARR_COUNT-1;i++)
- intBiTreeInit[i]=2*(i+1);
- }
- else
- return RET_ERR;
- //使最后兩數為無效值
- intBiTreeInit[ARR_COUNT-1]=NVALUE;
- intBiTreeInit[ARR_COUNT-2]=NVALUE;
(2)分析數組中的有效值
- //開始獲得數組中有效值位置
- int intRel=0;
- int intArr=0;
- for(intArr=0;intArr<=intCount-1;intArr++)
- {
- if(elemArr[intArr]!=elemNValue)
- {
- intRel++;
- vecIntEffPos.push_back(intArr);
- }
- }
(3)創建二叉樹節點
- //數組中有效值對應創建節點
- //同時初始化父子節點為NULL
- for(intArr=0;intArr<=intRel-1;intArr++)
- {
- pBiTreeTemp=(PBiTreeNode)malloc(sizeof(BiTreeNode));;
- if(NULL==pBiTreeTemp) //判斷是否有足夠的內存空間
- {
- cout<<"Memory alloc failure"<<endl;
- return RET_ERR;
- }
- //將有效值賦予節點
- pBiTreeTemp->BiTreeData=elemArr[vecIntEffPos[intArr]];
- //初始化左右子節點為null,便于后續的遍歷
- pBiTreeTemp->leftChild=NULL;
- pBiTreeTemp->rightChild=NULL;
- //先存節點值
- vecPBiTree.push_back(pBiTreeTemp);
//生成父子關系時最后一層不必遍歷,故理論循環上限可優化
- int intSubLast=0;
- intSubLast=intCount-(intCount+1)/2;
(5)構造二叉樹節點間的父子關系
- for(intArr=0;intArr<=intSubLast-1;intArr++)
- {
- //左右節點若存儲有效值則同時創建父子關系
- if(elemArr[intArr*2+1]!=elemNValue)
- vecPBiTree[intArr]->leftChild=vecPBiTree[intArr*2+1];
- if(elemArr[intArr*2+2]!=elemNValue)
- vecPBiTree[intArr]->rightChild=vecPBiTree[intArr*2+2];
(6)確實二叉樹根節點
- pBiTree=vecPBiTree[0];
轉化為左右子節點方式存儲后,則各種遍歷操作按大多數教程的常規方式處理即可,如前序遍歷函數:
- int BiTreePreTrace(PBiTreeNode &pBiTree)
- {
- //條件為非空樹
- if(pBiTree)
- {
- cout<<"Node value="<<(pBiTree->BiTreeData)<<endl;
- BiTreePreTrace(pBiTree->leftChild); //遍歷左子樹
- BiTreePreTrace(pBiTree->rightChild); //遍歷右子樹
- }
- return RET_OK;
- }
完整程序,請見附件文件。
http://files.cnblogs.com/vbspine/cnsDSExec.rar
*上述程序在Windows7x64,VS2008環境編譯運行通過
原文鏈接:http://www.cnblogs.com/vbspine/archive/2013/01/30/bitree.html
【編輯推薦】