隨著深度學(xué)習(xí)大語言模型的越來越火爆，大語言模型越做越大，使得其推理成本也水漲船高。模型量化，成為一個熱門的研究課題。

近日，字節(jié)跳動語音團隊推出一個全新的量化思路，拋棄傳統(tǒng)的量化范式，從數(shù)學(xué)優(yōu)化的角度來對量化任務(wù)建模。文章放在了 arXiv，代碼已經(jīng)開源，可以一鍵復(fù)現(xiàn)文中的所有結(jié)果：

• 論文鏈接：https://arxiv.org/abs/2404.12759
• 項目鏈接：https://github.com/bytedance/decoupleQ
• W2 算子：https://github.com/NVIDIA/TensorRT-LLM/pull/1568

1. 背景

大模型的迅速發(fā)展，使得推理成本越來越高。模型量化，作為一個降低推理成本的技術(shù)方案，得到了越來越多的關(guān)注與研究。然而，在傳統(tǒng)的量化范式下，模型的精度在極低比特下會迅速下降。基于此，作者們提出了一種新的量化思路，將模型參數(shù)解耦為整數(shù)部分和浮點部分，從數(shù)學(xué)優(yōu)化的角度來對量化任務(wù)建模，使得在極低比特下，模型依然能保持較高的精度。這樣做的優(yōu)勢是明顯的，我們不再需要關(guān)注量化特有的問題，比如如何處理敏感通道，如何處理 outlier 等等，而是只需要將量化問題進行數(shù)學(xué)建模，找到一個合適的優(yōu)化目標函數(shù)，然后去求解該函數(shù)。

2. 傳統(tǒng)量化

傳統(tǒng)上，我們對一個模型的量化思路是：

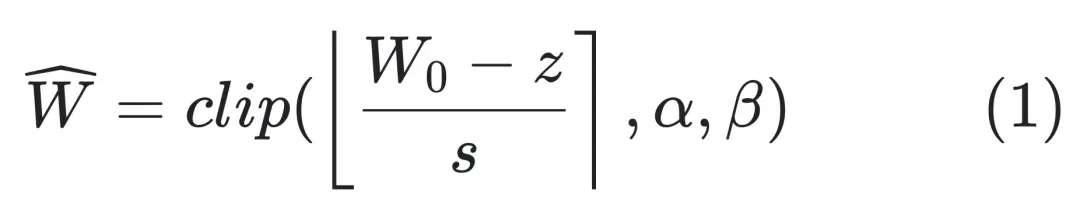
其中，

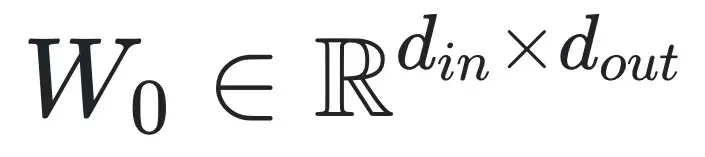
是量化前模型的浮點型 weights；s 和 z 是一個線性變換系數(shù)，表示 scale 和 zero point；α 和 β 是整數(shù)表示范圍的上下界，例如對于 int4 量化，可以取 α = -8, β = 7；

表示取整函數(shù)，一般是四舍五入到臨近的整數(shù)。

關(guān)于 s 和 z 的取值，一般來說，對于非對稱量化，我們可以取：

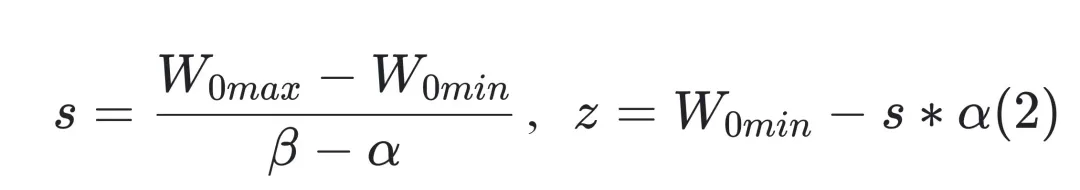
這樣就將一個分布在

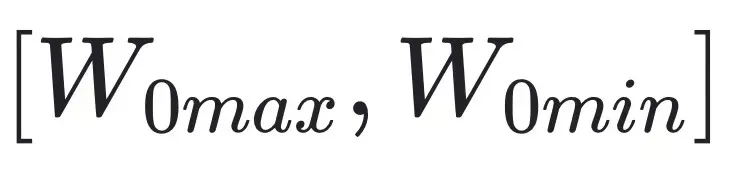
的浮點的 weights，線性映射到

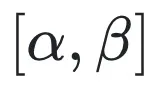
的區(qū)間范圍。

在反量化的時候，一般使用如下公式：

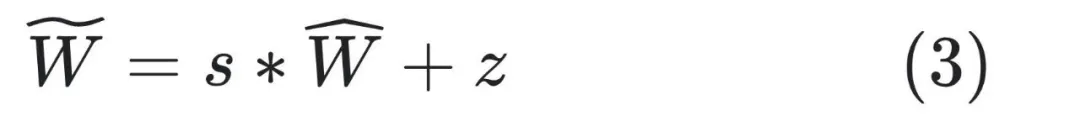
在這種傳統(tǒng)的量化方案中，我們需要關(guān)注很多量化特有的細枝末節(jié)問題，比如針對敏感通道，我們有敏感通道的處理方式；針對 outlier，我們有 outlier 的處理方式。這種頭痛醫(yī)頭腳痛醫(yī)腳的處理范式，難以應(yīng)付復(fù)雜多變的業(yè)務(wù)場景。字節(jié)跳動的研究者們試圖把這些問題都抽象出來，從一個宏觀的視角來看待量化問題。我們只需要建立一個抽象的優(yōu)化目標函數(shù)，再去求解這個目標函數(shù)即可。

3. decoupleQ

觀察 (1)~(3) 式在量化中的作用，如果我們換一種思路，就會發(fā)現(xiàn)其實我們不需要知道 (1) 式和 (2) 式。我們將一個大模型量化完畢以后，交付給下游引擎同學(xué)的時候，只需要知道 (3) 式中的

和 (s,z) 即可。也就是說，(3) 式中的 (s,z) 完全可以視作一個普通的仿射變換的系數(shù)，不需要保留其在 (2) 式中的含義。該仿射變換系數(shù)，可以通過數(shù)學(xué)優(yōu)化的方法求出來。

進一步挖掘 (3) 式中，我們可以將一個大模型的參數(shù)，解耦 (decouple) 成整數(shù)部分

和浮點部分 (s,z)。這樣解耦以后，模型量化的過程，就可以視作一個求解模型整數(shù)部分

和浮點部分 (s,z) 的過程。我們可以交替優(yōu)化求解。為此，要確定優(yōu)化目標函數(shù)和其約束條件。

對于一個 linear 層，我們可以構(gòu)建如下優(yōu)化目標函數(shù)：

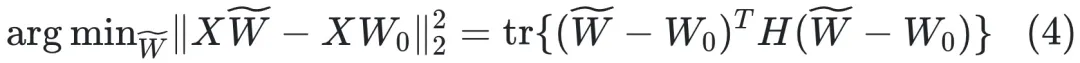
其中，

是該層的輸入，

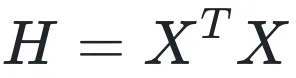
是一個對稱矩陣（若 X 的列都不全為零，則 H 是正定對稱矩陣）。

一般來說，為了提高量化精度，我們可以對模型的權(quán)重用 per-channel 量化。在 per-channel 量化中，在優(yōu)化 (4) 式的時候，

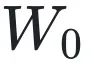
的各個列是獨立進行優(yōu)化的。所以我們只需要關(guān)注其中一列即可。

至此，優(yōu)化目標可以寫作如下：（為了符號簡潔，文章中重新定義符號）：

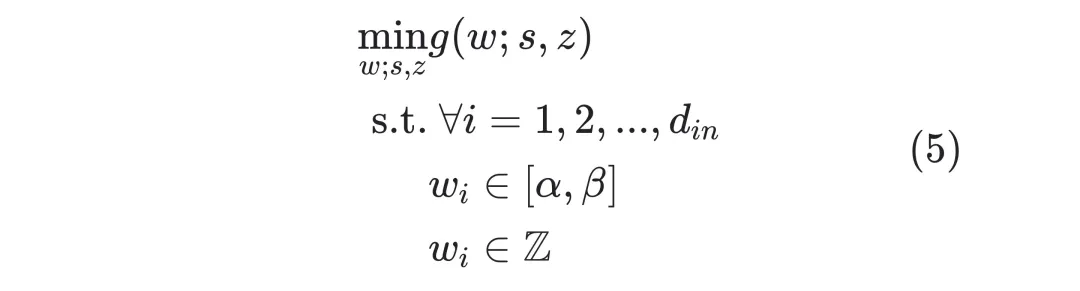
其中優(yōu)化目標函數(shù)為

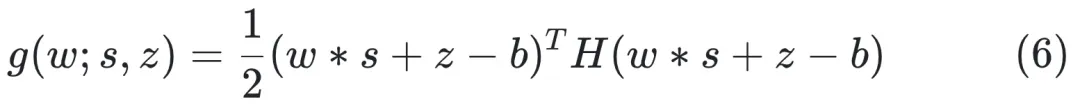
其中，w 是

的某一列，b 是

中對應(yīng)的列。其他符號的定義與前文相同。

事實上，優(yōu)化目標函數(shù) (6) 與 (4) 是完全一致的，

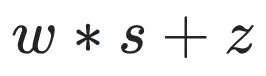
就是反量化過程。

將一個量化問題轉(zhuǎn)化為形如(5)式的數(shù)學(xué)優(yōu)化問題，正是 decoupleQ 區(qū)別于傳統(tǒng)量化論文的關(guān)鍵所在。這種轉(zhuǎn)化，使得我們只需要專注于求解 (5) 式即可，不再需要處理關(guān)于量化本身的細枝末節(jié)的問題，比如 outlier，等等。

式子 (5) 的求解并不容易，因為有關(guān)于

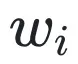
的約束的存在，特別是

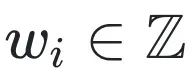
這個非凸約束。在論文中，作者給出一種交替求解的思路，即獲得關(guān)于 (s,z) 和 w 的良好的初始化以后，交替迭代求解 (s,z) 和 w。在求解 (s,z) 的時候，注意到式子 (5) 關(guān)于 (s,z) 是一個無約束的二次型，可以直接將目標函數(shù)求導(dǎo)，令導(dǎo)數(shù)為零，從而獲得解析解。在求解 w 的時候，作者采取了兩個層面的近似，第一層近似收斂性更高，但是求解慢；第二層近似采樣 GPTQ【1】的思想，收斂性稍差，但是求解更快。

為了進一步提升量化模型精度，作者指出，除了在 layer 層面做 mse 最小化以外，還可以在 block 層面做 mse 最小化，即：

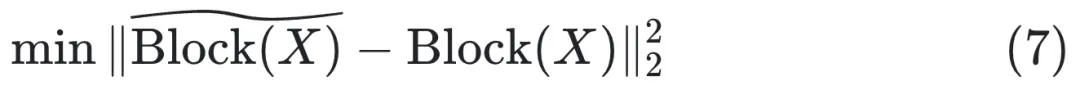
在這一步，作者在一個 transformer block 層面，將其中的各個 linear 層量化完畢以后，固定他們的整數(shù)部分

，而去微調(diào)浮點部分 (s,z) 以及 layer norm 的相關(guān)參數(shù)。實驗表面，這一步微調(diào)，能夠進一步提升模型精度。

4. W2 算子實現(xiàn)

要對量化后的模型進行推理，需要量化算子的支持，在業(yè)界沒有現(xiàn)成的 w2a16 的算子可用，作者們基于 Tensorrt-LLM 中的 w4 算子開發(fā)了 w2 的 Gemm cuda kernel, 實現(xiàn)了 w2a16 模型的高效推理。

量化模型本身是以 2bit weight 的形式加載和存儲在顯存中，因此會占用比較小的顯存。我們的 cuda kernel 通過在運行時將 2bit 的 weight 加載到寄存器中，再利用硬件指令高效轉(zhuǎn)換成 bf16 的形式與 activation 進行 gemm 運算。因為我們的場景受限于 latency, generation 階段的 batchsize 比較小，此時矩陣乘受限于 weight 的訪存，這種實現(xiàn)會大大減少訪存量，提升模型的性能。在實現(xiàn)過程中，結(jié)合了算法搜索以及 SpiltK Parallel Reduce，進一步能提升模型的性能，實測在 batchsize=1 的情況下，在 L 卡上 w2a16 Gemm 性能相比 w4a16 能提升 1.4x-1.7x 不等。

算子鏈接：https://github.com/NVIDIA/TensorRT-LLM/pull/1568

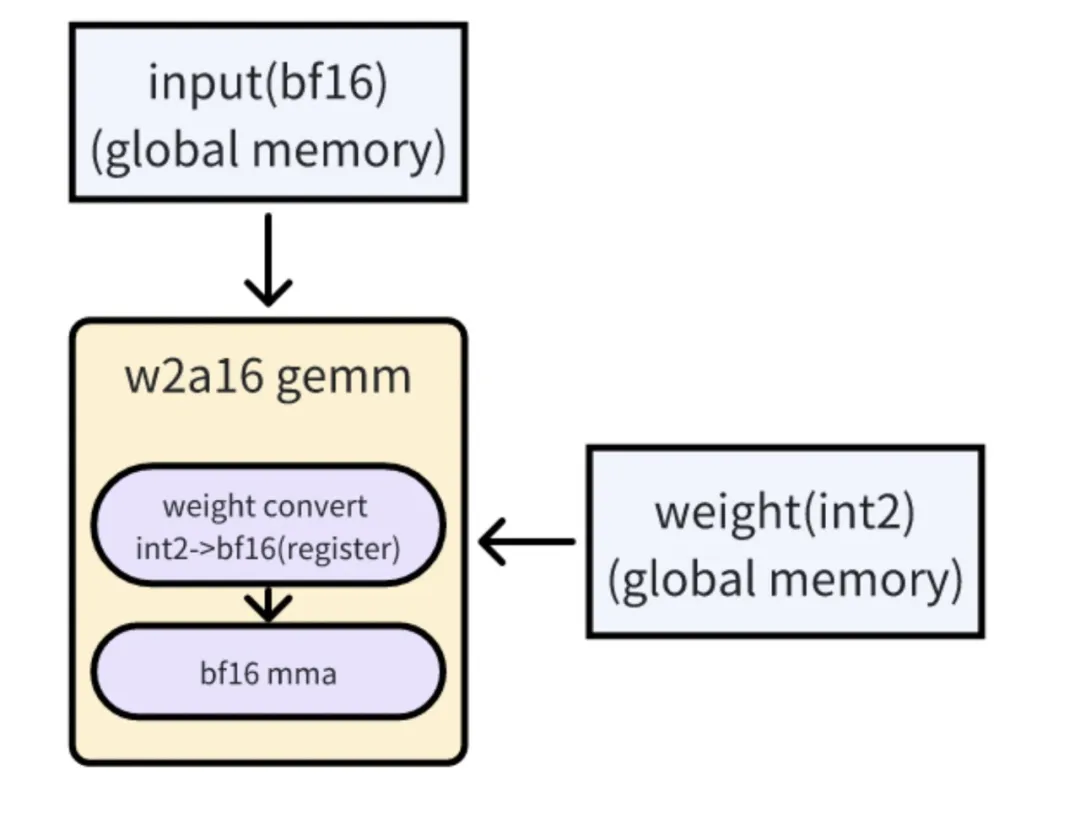
w2 cuda kernel的實現(xiàn)原理

5. 實驗

作者在文章給出了字節(jié)跳動內(nèi)部的 ASR 實驗結(jié)果，和開源的實驗對比結(jié)果：

其中內(nèi)部實驗結(jié)果是：

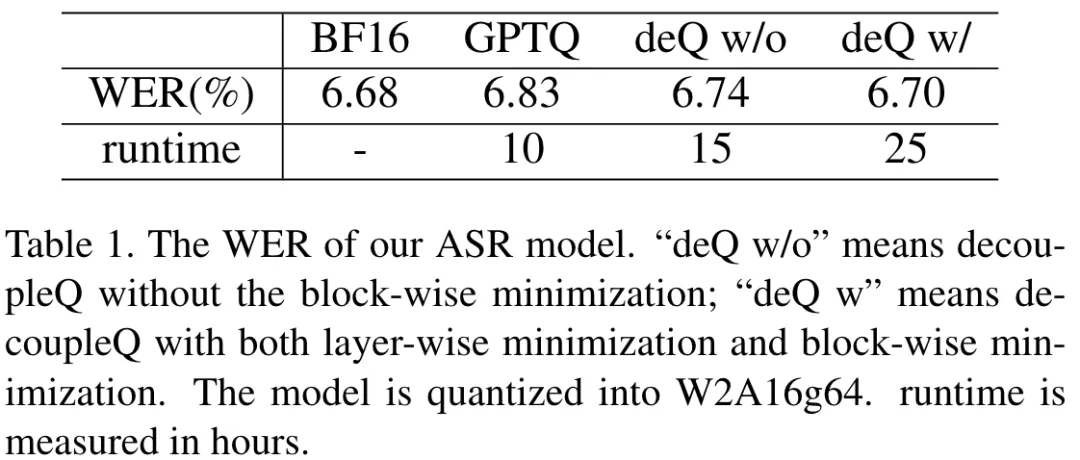
該表格中，作者用 word err rate (WER) 來衡量 ASR 的準確率。作者嘗試使用不同的方法將模型量化為 W2A16g64。量化前的浮點模型的 wer 是 6.68%，使用 GPTQ【1】量化以后是 6.83%，帶有 block 最小化的 decoupleQ 量化以后的 wer 是 6.70%，該結(jié)果與量化前的浮點模型的 wer 很接近。同時也 report 了量化所需要的耗時。量化高精度的代價，是量化耗時較長。在實際業(yè)務(wù)中，在使用 decoupleQ 對模型量化完畢以后，固定整數(shù)部分，使用有標簽數(shù)據(jù)集微調(diào) scale 和 zero，模模型精度有進一步的提升。

開源對比實驗結(jié)果是：

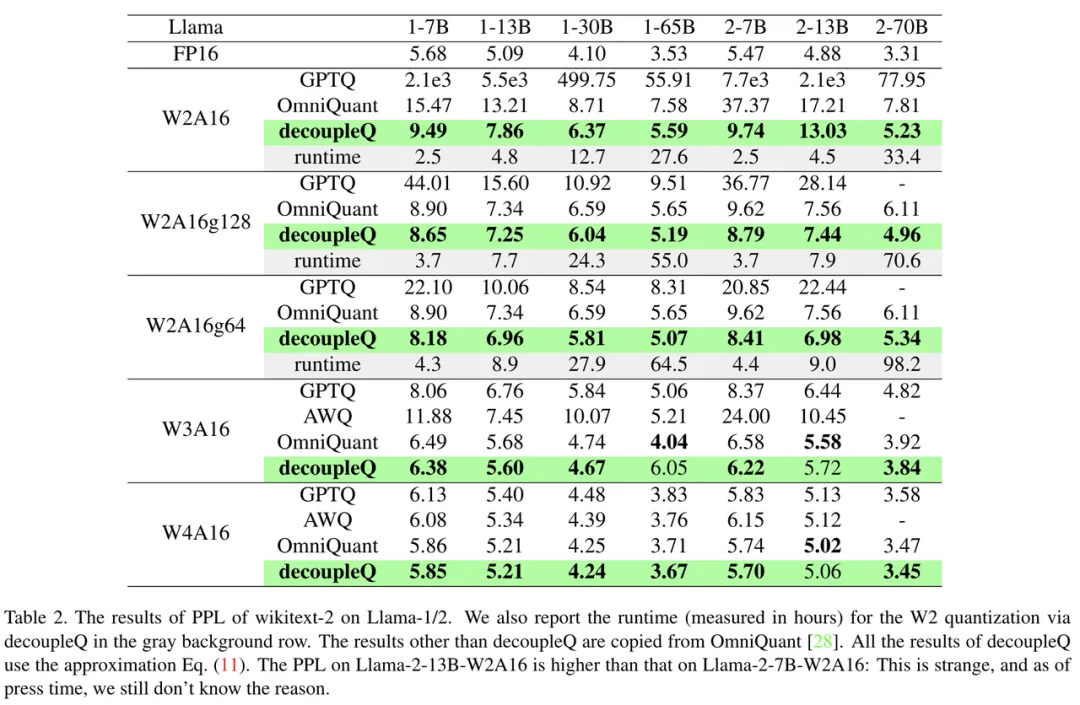
該表格是 decoupleQ 和其他方法在 Llama-1/2 上的量化結(jié)果比較。以 perplexity (PPL) 作為評價指標。可以看出，在同樣的量化配置下，deoucpleQ 的 PPL 在絕大多數(shù)時候會低于其他方法。

6. 業(yè)務(wù)收益

decoupleQ 量化技術(shù)在字節(jié)跳動語音部門現(xiàn)在被廣泛使用。已經(jīng)上線于語音生成模型（Text-to-Speech），語音識別模型（automic speech recognition）等等，落地于豆包、飛書、抖音等產(chǎn)品中。大量上線業(yè)務(wù)表明，基于 decoupleQ 的量化，W4A16 的推理精度已經(jīng)完全能和 fp16/bf16 推理持平；W2A16 的精度只略差于 fp16/bf16 精度（對浮點部分 sft 以后，精度能和 fp16/bf16 持平）。盡管論文中只介紹了 weight-only 的量化，但是在實際業(yè)務(wù)中，在 weight 獲得良好的量化以后，對 activation 的量化也便能簡單許多。

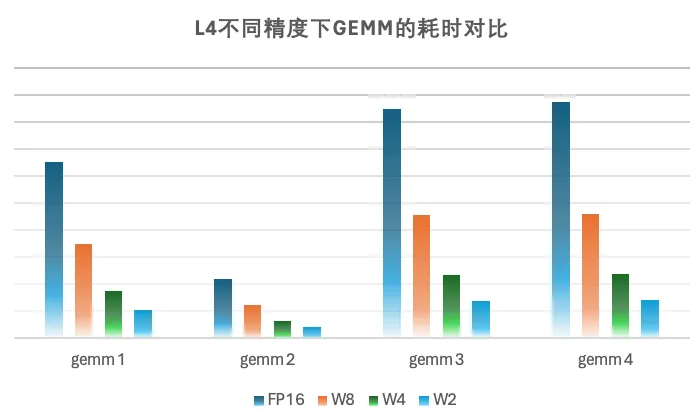
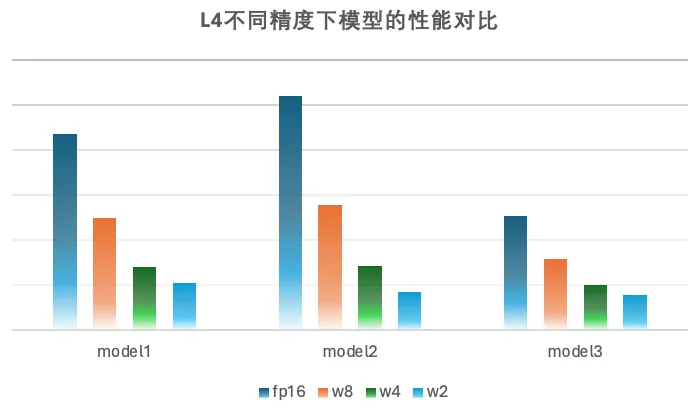
在硬件加速上相比 fp16、w8fp16、w4fp16 獲得了不錯的加速效果，在小 batch 下 w2 矩陣乘的性能相比 fp16 提升 5-6 倍，相比 w4 提升 1.5-1.7 倍。在內(nèi)部業(yè)務(wù)模型上，w2fp16 相比 fp16 性能有 3-5 倍的提升， 相比 w4fp16 性能有 1.25-1.4 倍的性能提升，同時也會使得模型 weight 占用顯存大幅下降，為 runtime 的顯存利用提供更多空間。

7. 總結(jié)與討論

在總結(jié)與討論部分，作者也指出了 decoupleQ 目前存在的兩個風(fēng)險：

1. decoupleQ 旨在使用數(shù)學(xué)優(yōu)化的手段，將量化前后的 L2 loss 最小化。然而，layer 層面或者 block 層面的 L2 loss 最小化，未必能夠代表最終模型精度的最優(yōu)；

2. 在 (5) 式和 (7) 式的優(yōu)化過程中，在求解

和 (s,z) 的時候，只針對一小部分校準數(shù)據(jù)來求解，這使得 decoupleQ 容易對校準數(shù)據(jù)過擬合。

盡管如此，作者也指出，將模型參數(shù)解耦為整數(shù)部分和浮點部分的思路，是很有意義的。如果有標簽數(shù)據(jù)集存在，我們可以量化完畢以后，固定整數(shù)部分，使用有標簽數(shù)據(jù)集來專門訓(xùn)練 (s,z)，以進一步提升模型的精度。這樣既保證了模型的泛化性能（源于固定整數(shù)部分

），又能在特定子任務(wù)上發(fā)揮能力（源于微調(diào)浮點部分）。在字節(jié)跳動的實際業(yè)務(wù)中，在上一版的模型量化完畢上線以后，下一版更新的時候，也可以只訓(xùn)練模型中的浮點部分。

本文轉(zhuǎn)自機器之心 ，作者：機器之心

原文鏈接:??https://mp.weixin.qq.com/s/tv4H0LA-e0qzX33NIWCdAg??