本文第一作者是西湖大學博士生馮睿騏，通訊作者為西湖大學人工智能系助理教授吳泰霖。吳泰霖實驗室專注于解決 AI 和科學交叉的核心問題，包含科學仿真、控制、科學發現。

在解決離線強化學習、圖片逆問題等任務中，對生成模型的能量引導（energy guidance）是一種可控的生成方法，它構造靈活，適用于各種任務，且允許無額外訓練條件生成模型。同時流匹配（flow matching）框架作為一種生成模型，近期在分子生成、圖片生成等領域中已經展現出巨大潛力。

然而，作為比擴散模型更一般的框架，流匹配允許從幾乎任意的源分布以及耦合分布中生成樣本。這在使得它更靈活的同時，也使得能量引導的實現與擴散模型有根本不同且更加復雜。因此，對于流匹配來說，如何得到具有理論保證的能量引導算法仍然是一個挑戰。

針對這一問題，作者從理論上推導得到全新能量引導理論框架，并進一步提出多樣的實際能量引導算法，可以根據任務特性進行靈活選擇。本工作的主要貢獻如下：

• 本工作首次提出了流匹配能量引導理論框架。
• 在本框架指導下，本工作提出三大類無需訓練的實用流匹配能量引導算法，并可將經典擴散模型能量引導算法包含為特例。
• 本工作給出了各個流匹配能量引導算法性能的理論分析和實驗比較，為實際應用提供指導。

• 論文標題：On the Guidance of Flow Matching
• 論文鏈接：https://arxiv.org/abs/2502.02150
• 項目地址：https://github.com/AI4Science-WestlakeU/flow_guidance

目前，本工作已被接受為 ICML 2025 spotlight poster，代碼已經開源。

研究背景

在生成模型的應用中，能量引導是一種重要的技術。理想情況下，它通過在模型已有的向量場中加上一個引導向量場，使生成的樣本服從的分布從訓練集分布改變為被某個能量函數加權后的分布。這樣一來，通過將能量函數設置為可控生成中的目標函數，即可使生成的樣本同時符合訓練集和滿足目標。

已有的能量引導算法集中于擴散模型，但是流匹配模型和擴散模型相比有本質上的差別，使得它們的能量引導算法不能直接通用。簡而言之，擴散模型可以被看作是流匹配模型在這些假設下的特例：源分布是高斯分布、源分布和生成分布之間沒有耦合、條件速度場滿足特定的線性形式。

在這些假設下，擴散模型的向量場可以和得分函數（score function）關聯起來，從而能量引導向量場可以被大大簡化，成為能量函數對數期望的梯度形式。在沒有這些假設時，能量引導向量場則需要幾乎完全重新推導。

目前雖然已經有一些工作對流匹配模型進行能量引導，但是這些流匹配模型仍然采用了高斯源分布等三個假設，所以本質上仍然是擴散模型（僅有條件向量場的系數中有細微不同）。因此，一個具有一般性的流匹配能量引導理論框架是必要的。

方法概述

首先，作者從流匹配模型基礎定義出發，推導了一般的流匹配能量引導向量場。具體而言，將疊加了能量引導后的總向量場與原向量場相減，

其中是源分布樣本，是目標分布樣本。經過化簡即可得到，

其中在實際數據集中可以近似為 1。

直觀上來說，引導向量場在能量函數小于它的平均值時將指向對應的，從而將原向量場轉向能量函數更小的區域。為了實現實際的能量引導，作者接下來提出三大類不同的無需訓練的能量引導算法。

蒙特卡洛估計

在引導向量場的計算中，主要困難來源于從中采樣。通過使用重要性采樣（importance sampling）技術，可以將從這一分布中采樣轉化為從更簡單的中采樣。從中采樣，只需從訓練數據集中采樣（如果可用），或者使用原模型生成服從的樣本。

利用這一方法，在樣本數不限的情況下可以計算精確的能量引導向量場。

梯度近似

為了更高效地計算引導向量場，可以通過近似來得到更簡單的形式。一個直接的近似是利用  在分布的均值附近的泰勒展開，通過只保留一階項來化簡。計算可得

也就是得到了擴散模型引導向量場中常見的「能量函數的梯度」的形式。注意到梯度前面的項和能量函數無關，可以進一步通過設置成超參數來近似，或者在一些特殊情況的流匹配模型中，可以被進一步簡化。

例如，通過采用源分布是高斯分布、源分布和生成分布之間沒有耦合、條件速度場滿足特定的線性形式的假設（即和擴散模型相同），可以簡化為經典的擴散后驗采樣（Diffusion Posterior Sampling, DPS）算法。

值得注意的是，雖然在擴散模型的特例中，最終形式和 DPS 相同，但是推導方式截然不同。DPS 基于擴散能量引導框架，利用 Jensen 不等式來消除不可計算的期望，但這里基于流匹配能量引導框架，則是使用泰勒展開來簡化這一期望的計算。

流匹配框架不僅提供了一個替代的理論理解視角，而且從中可以導出引導向量場的誤差上界。該誤差和的協方差矩陣（代表著當前噪聲樣本可以多準確地估計最終生成的干凈樣本），以及的 Hessian（代表著能量函數變化多劇烈）有關。

高斯近似

由于從中采樣困難，還可以直接假設是一個可以采樣的簡單分布，例如高斯分布。只需要將該高斯分布的均值和方差設置為和一致（甚至方差可以簡單設置為一個超參數），就可以期待從該高斯分布中采樣估計的引導向量場和真實引導向量場接近：

更進一步地，如果考慮具體任務中，能量函數的特定形式，比如含有高斯噪聲的線性逆問題中，

那么在該高斯近似下，可以計算引導向量場的解析表達式。

事實上，這和經典的偽逆引導擴散模型（GDM）的形式高度相似，在選取擴散模型對應的去噪進度超參數后可以完全簡化為 GDM。

實驗結果

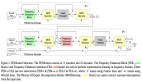
作者在合成數據、離線強化學習和圖片線性逆問題中進行了實驗。首先，在合成數據集上進行實驗。源分布被設置成圖中左一列的非高斯分布，并且能量函數包含簡單表達式（第一行）、關于極坐標下極角的階梯函數（第二行）、MLP 分類器的輸出（第三行）。

這些流匹配引導任務和擴散模型顯著不同，因此針對擴散模型的精確能量引導方法（左三列，對比能量引導 CEG）完全失敗。同時基于蒙特卡洛采樣的引導算法取得了最接近真實（ground truth）分布的結果，佐證了它是漸進精確的和流匹配引導框架的正確性。

此外，為了從實驗上比較各個引導算法優劣，作者還在離線強化學習（offline RL）和圖片線性逆問題任務中測試了各個引導生成算法的效果，結果如表所示。

總體來說，在離線強化學習任務中，蒙特卡洛采樣引導有最佳性能。這可能由于離線強化學習任務中需要同一個引導算法在不同時間步的條件下都產生穩定的引導采樣樣本，因此理論保證的能量引導算法具有最佳性能；而圖片逆問題中，針對此逆問題形式設計的高斯近似引導和 GDM 有最佳性能，而蒙特卡洛采樣引導由于問題維度較高不能產生合理的引導向量場。

結論

本工作針對流匹配模型中能量引導算法的空白，提出了一種新的能量引導的理論框架，并且提出幾類各有優劣的實用引導算法，適用于一般的流匹配模型。此外，通過理論分析和實驗對各個引導算法進行了比較，提供了實際應用指導。本工作希望為流匹配引導采樣和為生成模型的進一步應用提供理論基礎。