就在剛剛，南航、南通大學(xué)、牛津等機構(gòu)的研究者發(fā)現(xiàn)：通過高指令的推理指令，DeepSeek-R1有望解決數(shù)學(xué)上的NP-hard問題！

論文地址：https://arxiv.org/abs/2502.20545

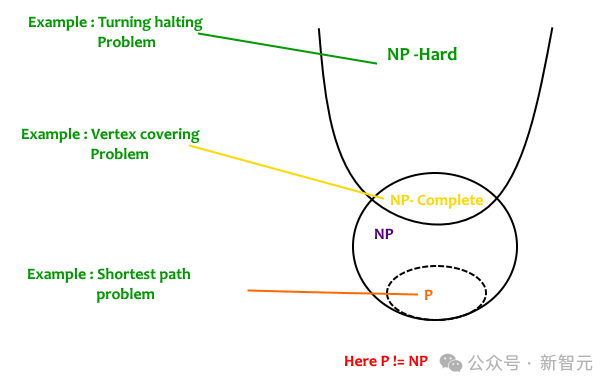
NP-hard問題，是計算復(fù)雜性理論中的一類問題。它們至少和NP問題一樣難，但不一定屬于NP類別（即不一定中多項式時間內(nèi)被驗證）。

本來，DeepSeek-R1、GPT-4o、OpenAI o1-mini這些模型，是做某種數(shù)學(xué)推理難題（SoS）是很困難的，正確率也就比純猜高一點。

但是，一旦給它們一些推理指導(dǎo)，所有的模型的推理能力立馬噌噌上漲，專業(yè)率最高提升了21%。

更令研究者們吃驚的是，Qwen2.5-14B-Instruct-1M在指導(dǎo)下，居然用了一個新奇精巧的方法，給出了一個此前從未見過的希爾伯特問題的反例：

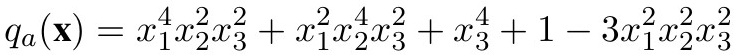
要知道，希爾伯特問題的反例，可并非簡單推導(dǎo)就能得出來的。

自1893年問題被提出之后，首個反例的發(fā)現(xiàn)耗時長達27年！

如今，卻被LLM短時間內(nèi)破解了。

研究者們大膽預(yù)言：照這個速度演進，LLM離破解NP-hard問題已經(jīng)很近了。

LLM能解決希爾伯特第十七問題嗎？

如今，LLM在眾多任務(wù)上，表現(xiàn)已經(jīng)接近人類水平，但它們在嚴(yán)謹(jǐn)數(shù)學(xué)問題求解上的能力，仍是不小的挑戰(zhàn)。

這次，研究者決定給大模型們來一個硬核難題——判斷給定的多元多項式是否為非負(fù)的。

這個問題，和希爾伯特第十七問題密切相關(guān)。后者由數(shù)學(xué)家希爾伯特在1900年提出后，立馬成為23個經(jīng)典數(shù)學(xué)問題之一。

而且，許多應(yīng)用數(shù)學(xué)和計算數(shù)學(xué)中的關(guān)鍵挑戰(zhàn)，都可以轉(zhuǎn)化為判斷某些多項式的非負(fù)性問題，比如控制理論、量子計算、多項式博弈、張量方法、組合優(yōu)化等。

然而，判斷一般多項式是否非負(fù)，是一個公認(rèn)的NP-hard問題！

即使對于相對低階或僅含少量變量的多項式，此問題仍然極具挑戰(zhàn)性。

怎么辦？為此，研究者們只能去尋找多項式的特殊類別，將復(fù)雜的非負(fù)性約束，替換成更簡單一些的條件。

由此，平方和（SoS）條件就登場了。

作為一項數(shù)學(xué)技術(shù)，它通過將多項式表示為若干平方項的和，提供了一種充分但非必要的非負(fù)性判定方法。

所以，OpenAI o1和DeepSeek-R1，能解決SoS條件規(guī)劃問題嗎？

用一個數(shù)據(jù)集，給LLM專業(yè)推理指導(dǎo)

為此，研究者構(gòu)建了SoS-1K數(shù)據(jù)集。

這個數(shù)據(jù)集經(jīng)過了精心策劃，包含約1,000個多項式，并配備了五個精心設(shè)計的專家級SoS專業(yè)推理指導(dǎo)。

具體包括：

• 多項式階數(shù)
• 主導(dǎo)搜索方向的非負(fù)性
• 特殊結(jié)構(gòu)的識別
• 平方形式表達的評估
• 單項式的二次形式矩陣分解

接下來，屬于SOTA模型們的考驗來了！

DeepSeek-R1、DeepSeek-V3、GPT-4o、OpenAI o1-mini、Qwen2.5 系列和 QwQ-32B-Preview在內(nèi)的多位明星大模型，接受了數(shù)學(xué)難題的洗禮。

研究者們得出了一系列有趣的發(fā)現(xiàn)。

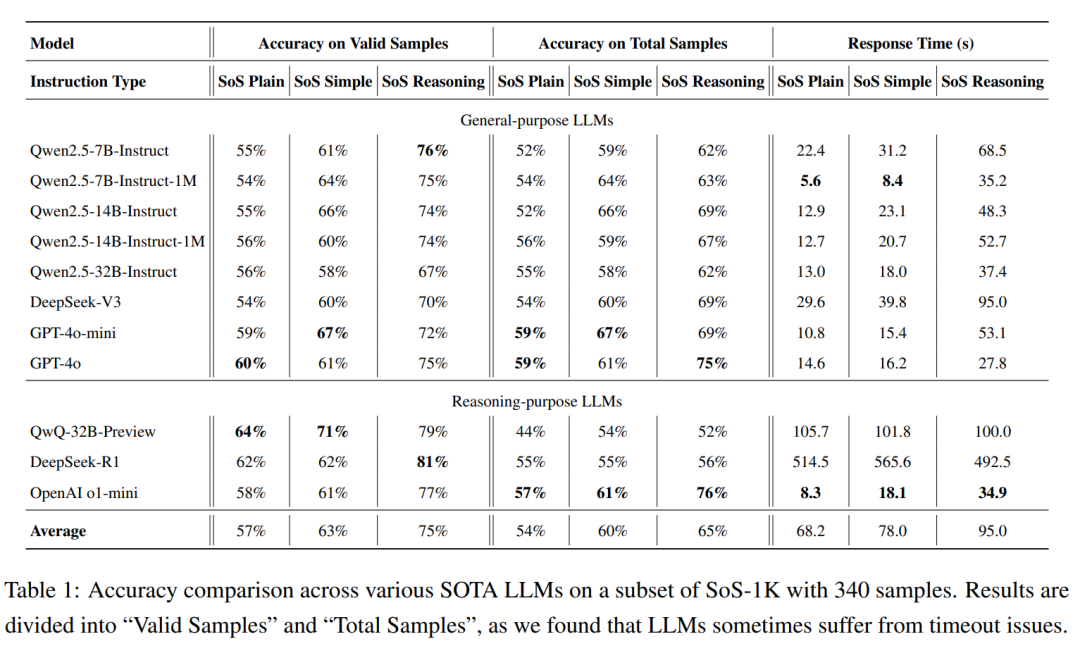
首先，如果未提供任何推理指導(dǎo)，所有的SOTA模型幾乎都無法解決SoS問題。

它們的準(zhǔn)確率基本都在60%，僅僅略高于50%的隨機猜測基線。

不過，一旦使用高質(zhì)量的推理軌跡進行提示，所有模型的準(zhǔn)確率就立馬有了顯著提升！

最高的提升了21%，而且推理質(zhì)量越高，模型表現(xiàn)就越好。

另外還有兩點發(fā)現(xiàn)：專注于推理的LLM通常優(yōu)于通用LLM，無論提示質(zhì)量如何。

參數(shù)較大的模型通常只用更少的推理步驟，就能正確預(yù)測，而小模型要達到最佳性能，就需要更多的推理過程了。

14B模型竟發(fā)現(xiàn)了此前未見的希爾伯特問題反例

然后，研究者還進一步證明，對一個預(yù)訓(xùn)練的7B模型在SoS1K數(shù)據(jù)集上進行4小時的監(jiān)督微調(diào)后，僅使用2張A100 GPU，就能讓它準(zhǔn)確率從54%暴增至70%，響應(yīng)速度也大幅提高。

其中，SoS-7B僅需DeepSeek-V3和GPT-4o-mini計算時間的1.8%和5%。

也就是說，這個7B模型超越了671B的DeepSeek-V3和GPT-4o-mini在內(nèi)的更大規(guī)模模型。

然后，驚人的結(jié)果來了——

當(dāng)模型被輸入高質(zhì)量的推理提示時，甚至在研究級問題上做出了革命性的突破。

比如，Qwen2.5-14B-Instruct-1M就利用Motzkin多項式，生成了全新的、此前未見的希爾伯特第十七問題的反例。

具體來說，模型是如何發(fā)現(xiàn)這個反例的？

研究者展示了以下過程：通過SoS Reasoning提示，Qwen-14B-1M推導(dǎo)出了一個新的有效NNSoS示例：

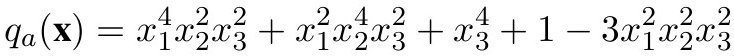
模型構(gòu)建這個例子的方法，非常新奇有趣，令研究者贊嘆不已。

它從NNSoS的著名例子開始，如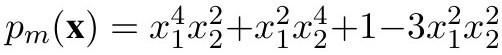：，然后，引入了一個新變量并稍微修改了系數(shù)，進而生成了q_a。

這也就給了我們極大信心：按照如今LLM展現(xiàn)出的推理能力，或許有朝一日，它們真能破解NP-hard問題。

值得一提的是，團隊只用2張英偉達A100 GPU，耗時4小時就完成了對Qwen2.5-7B-Instruct-1M的微調(diào)。

由此得到的SoS-7B模型達到了70%的總體準(zhǔn)確率，超過了671B參數(shù)量的DeepSeek-V3（69%），同時響應(yīng)時間僅需1.8秒，而DeepSeek-V3則需要100秒。

SoS-1K Dataset

首先，研究者對SoS多項式做出了定義。

隨后，研究者們?yōu)長LM精心設(shè)計了指令，從而提供了結(jié)構(gòu)化的分析框架，明確了約束條件，優(yōu)化了邏輯推理流程，讓它們顯著提高了解題能力。

為此，他們構(gòu)建了三種不同層次的的推理指令集。

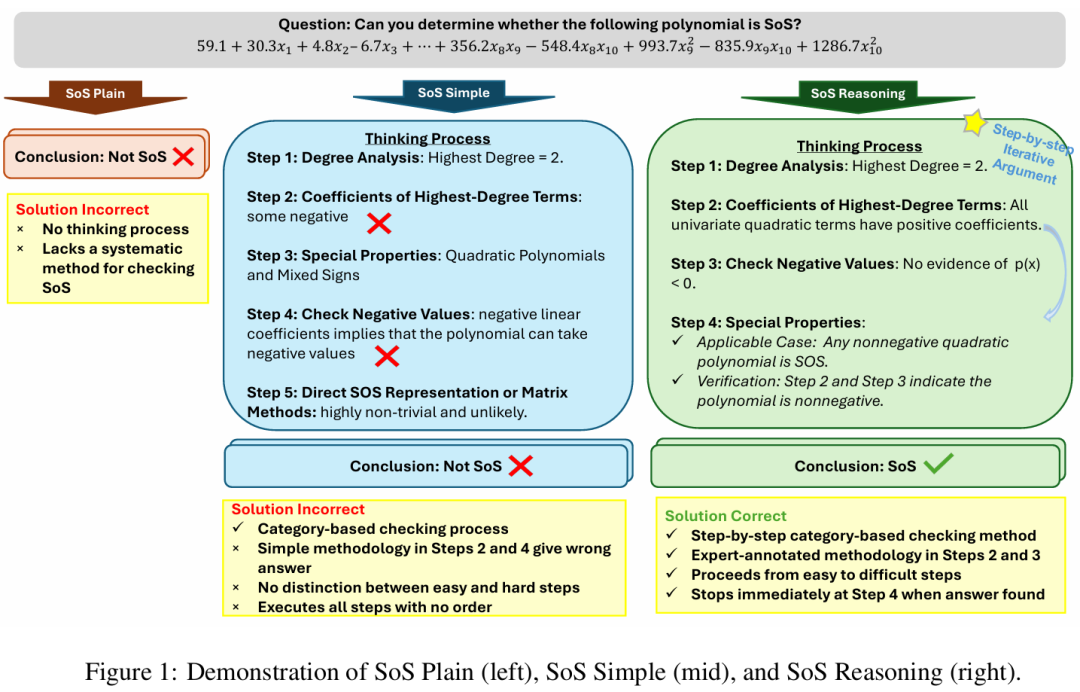
1. 基礎(chǔ)SoS指令（SoS Plain）

直接向LLM提問：「請分析該多項式是否可以表示為平方和（SoS）」？

2. 簡化SoS指令（SoS Simple）

將SoS多項式劃分為五個不同類別，每個類別由簡潔的一行標(biāo)準(zhǔn)定義。

3. 基于推理的完整SoS指令（SoS Reasoning）

這是一個結(jié)構(gòu)化的五步框架，用來系統(tǒng)化識別SoS多項式。

而就是這個SoS Reasoning，成為了LLM解決數(shù)學(xué)研究級問題的基礎(chǔ)，讓它們的能力擴展到更復(fù)雜的數(shù)學(xué)推理任務(wù)。

下面就是一個SoS Reasoning的示例。

• 步驟1. 檢查次數(shù)：SoS多項式的最高次數(shù)必須是偶數(shù)。
• 步驟2. 檢查非負(fù)性：SoS多項式對所有實數(shù)輸入都應(yīng)為非負(fù)值。
• 步驟3. 檢查已知特例：任何非負(fù)二次多項式以及任意一元或二元的非負(fù)四次多項式均為SoS。
• 步驟4. 檢查平方形式：根據(jù)定義2.1，SoS多項式可表示為：p_s(x) = ∑_i{q_i(x)2}。其中，每個q_i(x)均為多項式。
• 步驟5. 檢查矩陣分解：根據(jù)定理B.1，可以將多項式表示為：p(x) = y*?Qy*。其中，Q為對稱矩陣。隨后，檢查Q是否為半正定矩陣。

SoS任務(wù)上的LLM評估

在SoS-1K數(shù)據(jù)集中，研究者隨機抽取了約340道測試題，涵蓋了所有測試子類別。

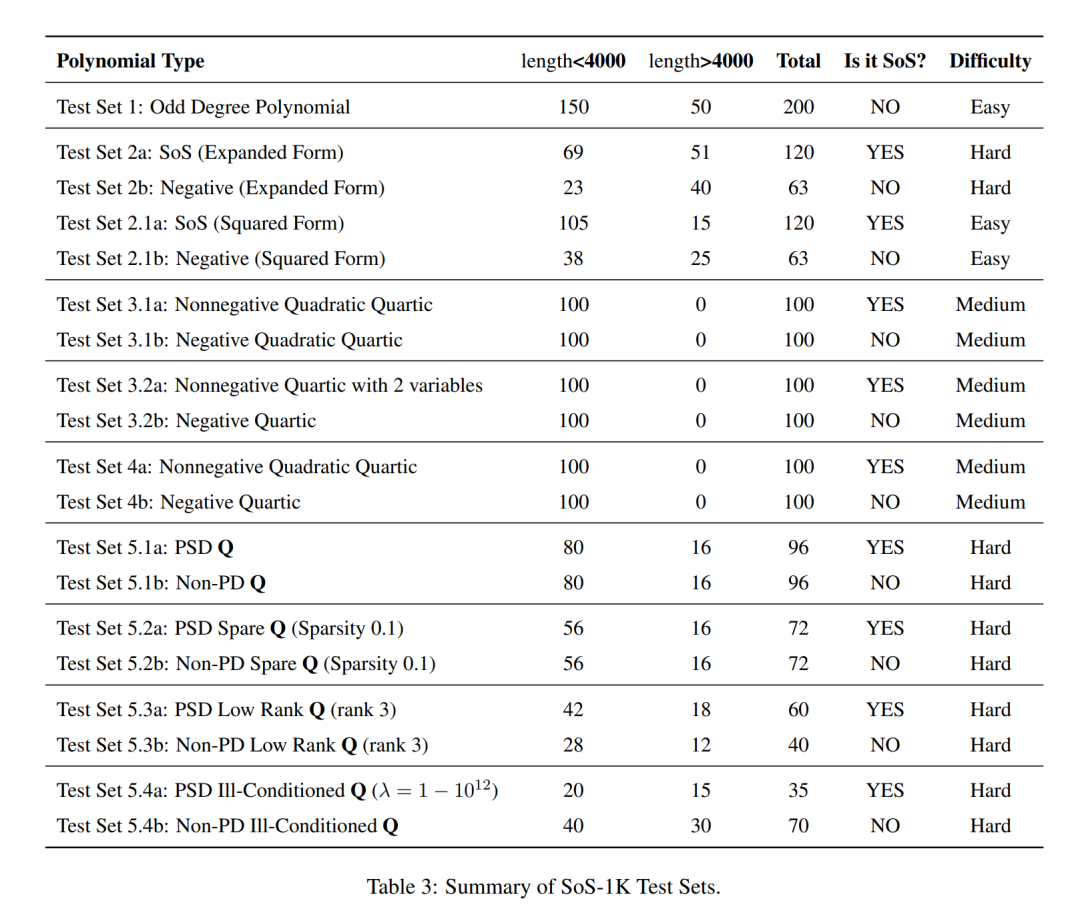
參與評估的有專門的推理模型（如DeepSeek-R1、OpenAI o1-mini 和QwQ-32B-Preview），以及通用大模型（如DeepSeek-V3、GPT-4o 和Qwen2.5系列）。

結(jié)果如下。

模型對SoS和非負(fù)性的理解

有人可能會問：

• 模型是只學(xué)會了分類，還是真正發(fā)展出了「思考」和「構(gòu)建」新證明和示例的能力？
• 當(dāng)面對SoS或多項式優(yōu)化中的研究問題時，模型能否生成具有數(shù)學(xué)意義的見解？

為了探索這一點，團隊設(shè)計了一系列研究導(dǎo)向的問題來測試模型理解SoS和非負(fù)性質(zhì)背后數(shù)學(xué)概念的能力。

比如，問Qwen-7B-1M和Qwen14B-1M：你能提供一個文獻中從未出現(xiàn)過的新NNSoS嗎？

有趣的是，當(dāng)使用SoS Plain提示時，Qwen-14B-1M只能給出文獻中已知的例子，而Qwen-7B-1M返回了一個不正確的答案：

雖然回答錯誤，但這個問題挑戰(zhàn)性極大，即便像YALMIP這樣的經(jīng)典求解器也無法提取全局最優(yōu)性。

然而，當(dāng)使用SoS Reasoning提示向模型提出相同的研究問題時，模型正確地識別出了pa不是問題的有效解。

這一改進源于SoS推理的第4步，其中模型認(rèn)識到p_a(x)是兩個變量的非負(fù)四次多項式，因此不可能是NNSoS。

進一步分析

Q1：模型是否遵循真正的數(shù)學(xué)逐步驗證過程？

結(jié)果顯示，LLM能夠按照SoS推理指令，一步一步生成邏輯和數(shù)學(xué)都正確的答案。

比如在下面這個例子中，o1-mini的回復(fù)不僅在邏輯上和數(shù)學(xué)上是正確的，而且一旦模型推導(dǎo)出答案就自然停止，而不是盲目地遍歷所有可能的步驟。

Q2：模型能否有效地從長文本多項式中提取關(guān)鍵信息？

與標(biāo)準(zhǔn)文本輸入不同，多項式是由變量、系數(shù)、指數(shù)和項組成的復(fù)雜代數(shù)表達式。因此，對于LLM來說，有效解釋和提取此類結(jié)構(gòu)化格式中的關(guān)鍵信息至關(guān)重要。

分析表明，雖然QwQ-32B-Preview在處理超過4K token長度的問題時會遇到困難，但大多數(shù)SOTA的模型都能夠成功地從4K長度的多項式中提取必要的系數(shù)進行評估，并生成正確的答案。

Q3：在SoS推理的第1步到第5步中，哪一步的準(zhǔn)確率有所提高？

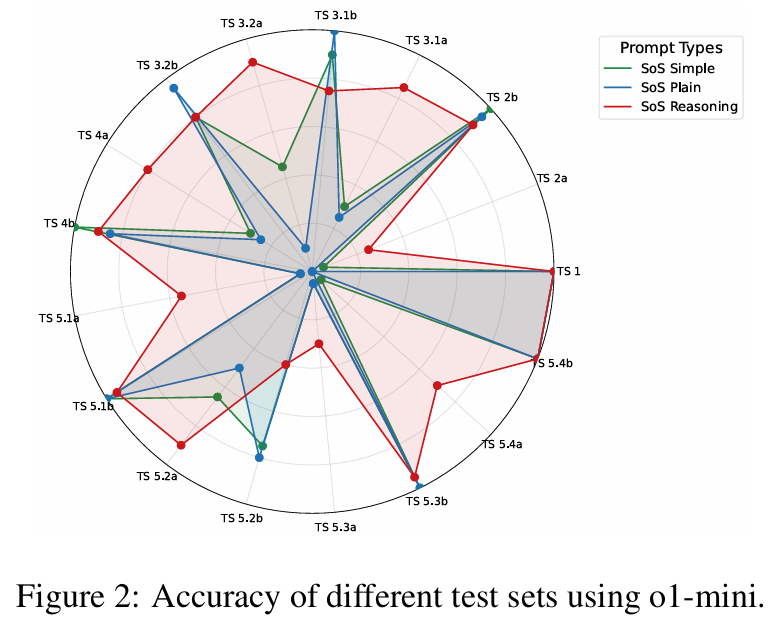
圖2展示了o1-mini模型在基礎(chǔ)SoS（SoS Plain）、簡化SoS（SoS Simple）和完整SoS推理（SoS Reasoning）下不同測試集的準(zhǔn)確率提升情況。

結(jié)果顯示，最簡單的Test Set 1（對應(yīng)步驟1）在所有提示方法下，都毫無意外地達到了100%的準(zhǔn)確率。

得益于步驟2和步驟5，對于更具挑戰(zhàn)性的Test Sets 2a、3.1a、5.1a–5.4a，從基礎(chǔ)SoS到簡化SoS再到完整SoS推理，也都有持續(xù)的改進。

因為，這些步驟引入了一系列用于非負(fù)性驗證的數(shù)學(xué)方法，包括常數(shù)系數(shù)檢查、網(wǎng)格求值、首項和主導(dǎo)項比較、尋找最小值、矩陣分解以及尋找對稱性和平移。

Q4：模型在推理過程中會「偷懶」嗎？

是的，在SoS推理提示下觀察到的另一個有趣現(xiàn)象是，模型在執(zhí)行第5步時往往會「走捷徑」。

具體而言，它通常會避免完全執(zhí)行第5步中的矩陣分解或半正定規(guī)劃（SDP）等復(fù)雜操作，而是基于前面步驟的結(jié)果推測答案。這種行為在處理長輸入和復(fù)雜多項式時尤為普遍。

對于較簡單的問題，推理模型如o1-mini（運行時間最短，為17秒）和較大的模型如QwQ-32B-Preview往往會采取捷徑，跳過第5步，從前面更簡單的步驟中推斷答案。

而DeepSeek-V3則不會走捷徑，而是花費明顯更多的時間（40秒）正確地解決所有步驟。

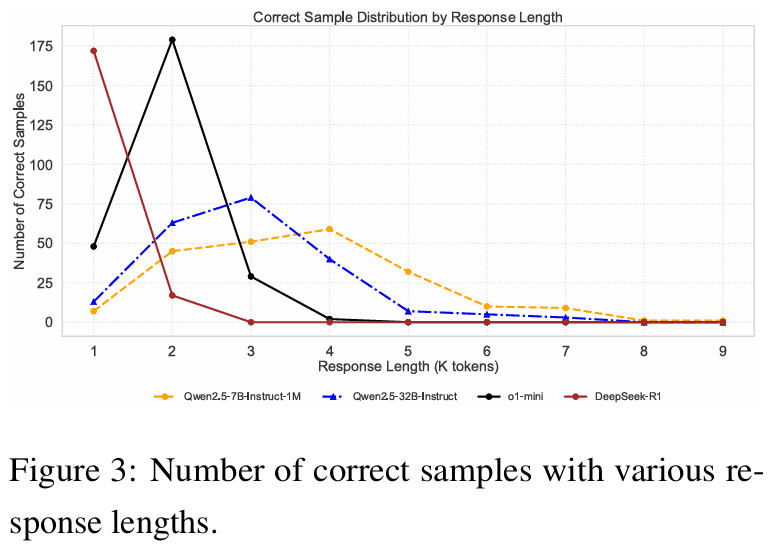
Q5：推理長度如何影響準(zhǔn)確性？

如圖3所示，更高性能的模型通常需要更少的思考所需token數(shù)量來做出正確預(yù)測，而性能較低的模型需要更多的推理步驟才行。

例如，DeepSeek-R1和o1-mini在1K-2K的輸出長度下，就達到最高的正確預(yù)測數(shù)量；而Qwen2.5系列需要3K-4K個token才能產(chǎn)生正確答案。

Q6：當(dāng)前的SOTA模型有什么局限性？

首先，對于長輸入情況，會出現(xiàn)無效樣本。例如，在DeepSeek-R1中，340個樣本中只有234個是有效的。

其次，在處理復(fù)雜問題時，「走捷徑」雖然會節(jié)省時間，但在困難步驟時過早停止并猜測答案，會對準(zhǔn)確性產(chǎn)生負(fù)面影響。

第三，雖然這些模型在處理小型多項式時表現(xiàn)出色（準(zhǔn)確率接近90%），但在多項式的二次型涉及低秩矩陣分解時，表現(xiàn)不佳。