使用Python實現基于矩陣分解的長期事件(MFLEs)時間序列分析
在現代數據分析領域,時間序列數據的處理和預測一直是一個具有挑戰性的問題。隨著物聯網設備、金融交易系統和工業傳感器的普及,我們面臨著越來越多的高維時間序列數據。這些數據不僅維度高,而且往往包含復雜的時間依賴關系和潛在模式。傳統的時間序列分析方法如移動平均等,在處理此類數據時往往顯得力不從心。

基于矩陣分解的長期事件(Matrix Factorization for Long-term Events, MFLEs)分析技術應運而生。這種方法結合了矩陣分解的降維能力和時間序列分析的特性,為處理大規模時間序列數據提供了一個有效的解決方案。
核心概念
矩陣分解
矩陣分解(Matrix Factorization)是將一個矩陣分解為多個基礎矩陣的乘積的過程。在時間序列分析中,最常用的是奇異值分解(Singular Value Decomposition, SVD)。SVD可以將原始矩陣 A 分解為:
A = USV^T
其中:
- U 和 V 是正交矩陣
- S 是對角矩陣,對角線上的元素稱為奇異值
潛在變量與潛在特征
- 潛在變量(Latent Variables):指數據中無法直接觀測但實際存在的變量,它們往往是多個可觀測變量的綜合表現。
- 潛在特征(Latent Features):通過矩陣分解得到的低維表示,它們是潛在變量在數學上的具體體現。每個潛在特征可能代表多個原始特征的組合。
維度降低在時間序列分析中的意義
維度降低(Dimensionality Reduction)在時間序列分析中具有多重意義:
計算效率:
- 原始維度下的計算復雜度:O(n^3),其中n為特征數量
- 降維后的計算復雜度:O(k^3),其中k為降低后的維度數,通常k << n
噪聲過濾:
- 較小的奇異值通常對應噪聲分量
- 保留主要奇異值可以實現數據去噪
模式提取:
- 幫助發現時間序列中的主要趨勢和季節性模式
- 便于識別多個時間序列之間的相關性
主成分分析(PCA)與MFLE的關系
主成分分析(Principal Component Analysis, PCA)是一種經典的降維方法,而MFLE可以看作是PCA在時間序列領域的擴展應用。與PCA相比,MFLE具有以下特點:
- 時間敏感性:考慮數據點之間的時間依賴關系
- 預測能力:能夠基于歷史模式進行預測
- 多序列建模:可以同時處理多個相關的時間序列
MFLE的數學基礎
MFLE的核心思想是將時間序列數據矩陣 X ∈ ?^(m×n) 分解為兩個低維矩陣的乘積:
X ≈ WH
其中:
- W ∈ ?^(m×k) 表示基矩陣(basis matrix)
- H ∈ ?^(k×n) 表示編碼矩陣(encoding matrix)
- k 是潛在特征的數量,通常 k << min(m,n)
這種分解通過最小化以下目標函數來實現:
min ||X - WH||F^2 + λ(||W||F^2 + ||H||_F^2)
其中:
- ||·||_F 表示Frobenius范數
- λ 是正則化參數,用于防止過擬合
長期事件(MFLEs)技術實現
數據準備與預處理
import numpy as np
import pandas as pd
from sklearn.decomposition import TruncatedSVD
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# 生成合成數據
np.random.seed(42)
n_series = 100 # 時間序列的數量
n_timepoints = 50 # 時間點的數量
# 模擬數據矩陣(行:時間序列,列:時間點)
data_matrix = np.random.rand(n_series, n_timepoints)
df = pd.DataFrame(data_matrix)
print(df.head())在這個實現中,我們選擇了100個時間序列,每個序列包含50個時間點。這些參數的選擇基于以下考慮:
- n_series = 100:提供足夠的樣本量以捕獲不同的模式
- n_timepoints = 50:足夠長以體現時間序列的特性,又不會造成過大的計算負擔
矩陣分解實現
svd = TruncatedSVD(n_components=10) # 降至10個潛在特征
latent_features = svd.fit_transform(data_matrix)
# 重構時間序列
reconstructed_matrix = svd.inverse_transform(latent_features)關鍵參數說明:
n_components = 10
- 選擇理由:通常選擇能解釋80-90%方差的特征數量
- 計算成本:與特征數量的三次方成正比
- 最佳實踐:可以通過explained_variance_ratio_確定
截斷SVD(TruncatedSVD)
- 優勢:內存效率高,計算速度快
- 適用場景:大規模稀疏矩陣
- 數學原理:只計算前k個最大奇異值
預測模型構建
# 準備訓練和測試數據集
X = latent_features[:, :-1]
y = latent_features[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 訓練回歸模型
model = LinearRegression()
model.fit(X_train, y_train)
# 進行預測
y_pred = model.predict(X_test)模型選擇考慮:
線性回歸
- 優勢:計算效率高,可解釋性強
- 局限:僅能捕獲線性關系
- 適用場景:潛在特征間的關系較為簡單時
數據分割(test_size=0.2)
- 標準做法:留出20%作為測試集
- 注意事項:需要考慮時間序列的連續性
可視化分析
單序列重構效果分析
"""
原始與重構時間序列的對比
"""
import matplotlib.pyplot as plt
# 繪制原始與重構時間序列的對比圖
series_idx = 0 # 選擇特定的時間序列
plt.figure(figsize=(10, 6))
plt.plot(data_matrix[series_idx, :], label="Original", marker="o")
plt.plot(reconstructed_matrix[series_idx, :], label="Reconstructed", linestyle="--")
plt.title("MFLE: Original vs Reconstructed Time Series")
plt.xlabel("Time")
plt.ylabel("Values")
plt.legend()
plt.grid()
plt.show()
可視化結果解讀:
重構質量評估
- 曲線吻合度反映了模型捕獲主要模式的能力
- 偏差主要出現在局部波動處
- 整體趨勢被很好地保留
噪聲過濾效果
- 重構序列更平滑
- 去除了高頻波動
- 保留了主要趨勢
綜合性能評估
import matplotlib.pyplot as plt
import seaborn as sns
# 設置繪圖
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('Time Series Analysis and Prediction', fontsize=16)
# 1. 原始數據與重構數據對比(第一個時間序列)
axes[0, 0].plot(data_matrix[:1].T, 'b-', alpha=0.5, label='Original')
axes[0, 0].plot(reconstructed_matrix[:1].T, color="Red", label='Reconstructed')
axes[0, 0].set_title('Original vs. Reconstructed Data')
axes[0, 0].set_xlabel('Time Points')
axes[0, 0].set_ylabel('Value')
axes[0, 0].legend()
# 2. 解釋方差比
explained_variance_ratio = svd.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)
axes[0, 1].plot(range(1, len(explained_variance_ratio) + 1), cumulative_variance_ratio, 'bo-')
axes[0, 1].set_title('Cumulative Explained Variance Ratio')
axes[0, 1].set_xlabel('Number of Components')
axes[0, 1].set_ylabel('Cumulative Explained Variance Ratio')
axes[0, 1].set_ylim([0, 1])
# 3. 實際值與預測值對比
axes[1, 0].scatter(y_test, y_pred)
axes[1, 0].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
axes[1, 0].set_title('Actual vs. Predicted Values')
axes[1, 0].set_xlabel('Actual Values')
axes[1, 0].set_ylabel('Predicted Values')
# 4. 殘差圖
residuals = y_test - y_pred
axes[1, 1].scatter(y_pred, residuals)
axes[1, 1].axhline(y=0, color='r', linestyle='--')
axes[1, 1].set_title('Residual Plot')
axes[1, 1].set_xlabel('Predicted Values')
axes[1, 1].set_ylabel('Residuals')
plt.tight_layout()
plt.show()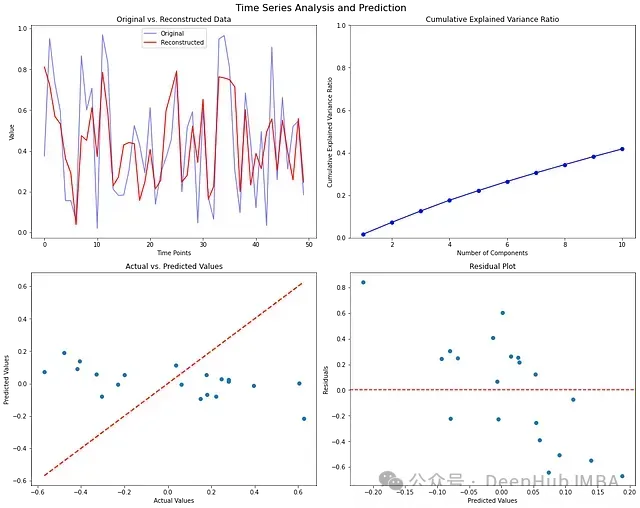
多圖表分析:
解釋方差比分析
- 累積方差比反映了信息保留程度
- 拐點可用于確定最優特征數量
- 通常在90%處截斷較為合理
預測性能評估
- 散點圖集中在對角線附近表示預測準確
- 殘差圖用于檢測系統性偏差
- 殘差的分布特征反映了模型假設的合理性
與其他時間序列分析方法對比
傳統統計方法對比
ARIMA模型
- 優勢:適合單變量時間序列,模型解釋性強
- 局限:難以處理高維數據,計算復雜度高
- 對比:MFLE在處理多變量時更有效率
指數平滑法
- 優勢:計算簡單,適合短期預測
- 局限:無法捕獲復雜的時間依賴關系
- 對比:MFLE能夠發現更深層的數據結構
深度學習方法對比
LSTM網絡
- 優勢:能夠學習復雜的時序依賴
- 局限:需要大量訓練數據,計算資源消耗大
- 對比:MFLE在計算效率和可解釋性方面更具優勢
時序自編碼器
- 優勢:能夠學習非線性特征
- 局限:模型復雜,訓練不穩定
- 對比:MFLE提供了更簡單且可解釋的解決方案
總結
時間序列數據的高維特性和復雜的時間依賴關系使其分析具有挑戰性。MFLE通過結合矩陣分解和時間序列分析的優勢,為這類問題提供了一個有效的解決方案。
通過對MFLE的深入理解和合理應用,可以在眾多實際場景中獲得良好的分析效果。未來隨著算法的改進和計算能力的提升,MFLE的應用范圍將進一步擴大。