素?cái)?shù)分布規(guī)律又有新發(fā)現(xiàn)！趙宇飛學(xué)生與牛津教授合作成果

作者：量子位 2024-12-23 10:00:00

多倫多大學(xué)教授John Friedlander評(píng)價(jià)說(shuō)，索尼和格林的這項(xiàng)研究表明高爾斯范數(shù)可以作為新領(lǐng)域的強(qiáng)大工具。

趙宇飛高材生、哥倫比亞大學(xué)助理教授Mehtaab Sawhney（索尼），又為數(shù)學(xué)界貢獻(xiàn)了一項(xiàng)重要成果——

與牛津大學(xué)教授Ben Green（格林）一起，證明了一項(xiàng)關(guān)于素?cái)?shù)分布的新規(guī)律。

關(guān)鍵是證明中用到了與Gowers范數(shù)相關(guān)的技術(shù)，而Gowers范數(shù)一開(kāi)始是拿來(lái)研究等差數(shù)列的，看上去和素?cái)?shù)規(guī)律風(fēng)馬牛不相及。

甚至作者索尼自己也表示，“作為一個(gè)‘局外人’，幾乎不可能判斷出這些事情是相關(guān)的”。

所以，這項(xiàng)研究不僅在素?cái)?shù)領(lǐng)域是一項(xiàng)重要工作，也揭開(kāi)了高爾斯范數(shù)的應(yīng)用潛能。

多倫多大學(xué)教授John Friedlander評(píng)價(jià)說(shuō)，索尼和格林的這項(xiàng)研究表明高爾斯范數(shù)可以作為新領(lǐng)域的強(qiáng)大工具。

最早和陶哲軒一同將素?cái)?shù)和Gowers范數(shù)聯(lián)系到一起的數(shù)學(xué)家Tamar Ziegler（齊格勒），也對(duì)索尼和格林的研究給予了高度評(píng)價(jià)：

看到我前一段時(shí)間想到的東西有了意想不到的新應(yīng)用，讓我覺(jué)得很有趣。

證明素?cái)?shù)分布新規(guī)律

2018年，F(xiàn)riedlander和美國(guó)羅格斯大學(xué)的Iwaniec提出了“高斯素?cái)?shù)猜想”（Gaussian primes conjecture）：

存在無(wú)窮多個(gè)素?cái)?shù)p、q，使得p2+4q2也是素?cái)?shù)。

（Friedlander和Iwaniec的合作可以追溯到上個(gè)世紀(jì)，1997年他們一同證明了a2+b?可以組成無(wú)數(shù)個(gè)素?cái)?shù)）

格林和索尼不僅證明了這一猜想，還將其推廣到了更多的情況——

對(duì)于滿(mǎn)足n≡0或n≡4(mod 6)的正整數(shù)n，均存在無(wú)窮多個(gè)素?cái)?shù)p和q使得p2+nq2也是素?cái)?shù)。

同時(shí)，格林和索尼還為這些素?cái)?shù)的數(shù)量給出了漸近公式：

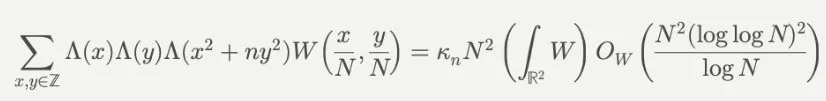
其中∧(n)是von Mangoldt函數(shù)，用于檢測(cè)n是否為素?cái)?shù)或素?cái)?shù)的冪，N>1，W為權(quán)函數(shù)，κ_n是一個(gè)與n有關(guān)的常數(shù)：

顯然，滿(mǎn)足條件的素?cái)?shù)數(shù)量不可能通過(guò)直接計(jì)算得到。

于是，格林和索尼選擇先將要證明的結(jié)論弱化，也就是先放寬一下約束條件——先將p和q的范圍放寬到“粗略素?cái)?shù)”。

舉個(gè)例子，如果我們要找出1-200之間的“粗略素?cái)?shù)”，可以找到與2、3、5、7這幾個(gè)小素?cái)?shù)同時(shí)互素（最大公因數(shù)為1）的數(shù)，這些數(shù)字即為1-200之間的“粗略素?cái)?shù)”。

（這些“粗略素?cái)?shù)”當(dāng)中，實(shí)際上不是素?cái)?shù)的數(shù)，算上1也只有5個(gè)。）

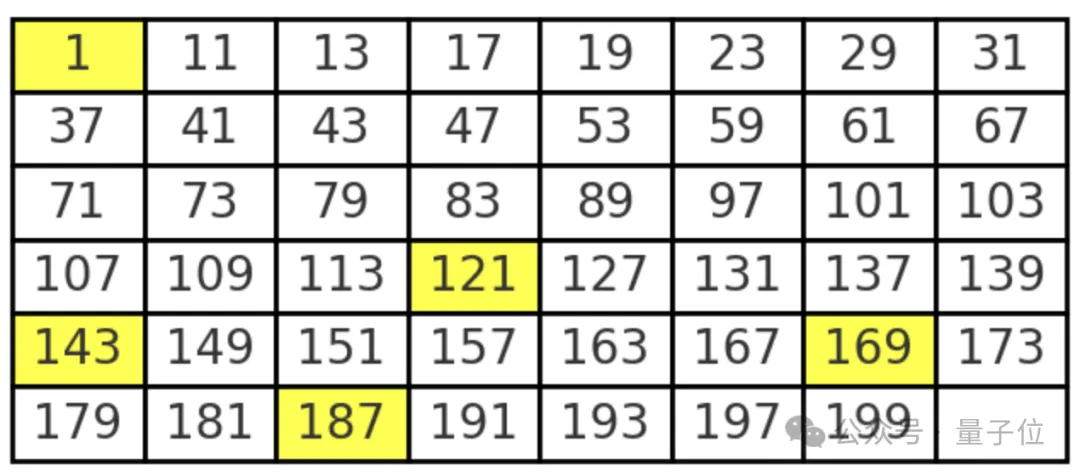
格林和索尼證明，通過(guò)對(duì)兩個(gè)“粗略素?cái)?shù)”進(jìn)行平方并將它們相加，可以得到無(wú)限多個(gè)素?cái)?shù)。

接下來(lái)，他們就需要證明使用“粗略素?cái)?shù)”構(gòu)建的集合，和使用真實(shí)素?cái)?shù)構(gòu)建的集合“足夠相似”。

其中就涉及了最關(guān)鍵的技術(shù)突破——Gowers范數(shù)的使用。

Gowers范數(shù)是一種測(cè)量函數(shù)“偽隨機(jī)性”的工具，2001年由數(shù)學(xué)家蒂莫西·高爾斯（Timothy Gowers）提出。

2018年，陶哲軒和塔瑪爾·齊格勒（Tamar Ziegler）找到了一種將高爾斯范數(shù)與“Type I和”與“Type II和”之間聯(lián)系起來(lái)的方法。

具體到這項(xiàng)研究，作者首先通過(guò)篩法將問(wèn)題簡(jiǎn)化為“Type I和”（左）與“Type II和”（右）的估計(jì)：

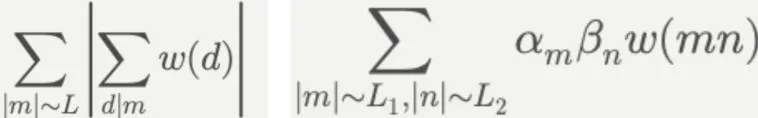
篩法的核心思想是，通過(guò)對(duì)這兩類(lèi)和的估計(jì)，過(guò)濾掉不滿(mǎn)足素?cái)?shù)條件的數(shù)，從而集中分析那些可能使p2+nq2為素?cái)?shù)的數(shù)值。

其中，“Type I和”聚焦于單個(gè)變量的局部分布，幫助處理低階貢獻(xiàn)；“Type II和”則關(guān)注雙變量交互，處理高階分布。

進(jìn)一步地，作者將問(wèn)題轉(zhuǎn)化到二次虛數(shù)域Q(√(-n))，并利用數(shù)域中的理想分解、范數(shù)分布以及素理想的性質(zhì)來(lái)研究目標(biāo)數(shù)列的素?cái)?shù)性。

具體來(lái)說(shuō)，在整數(shù)環(huán)Z中，研究x2+ ny2是否為素?cái)?shù)，等價(jià)于在Q(√(-n))中分析主理想x+y√(-n)是否為素理想。

接下來(lái)就輪到Gowers范數(shù)登場(chǎng)了。

為了控制“Type II和”，論文定義了函數(shù)f(x)和f’(y)，其中∧_Cramér(x) 是von Mangoldt函數(shù)的低復(fù)雜度近似：

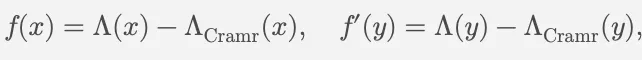
作者通過(guò)引入連接定理和逆定理，使用Gowers范數(shù)分析f(x)和f’(y)的偽隨機(jī)性，從而證明了它們?cè)诖蟛糠智闆r下對(duì)二次型x2+ ny2的貢獻(xiàn)是可控的。

也就是說(shuō)，作者通過(guò)篩法和Gowers范數(shù)，證明了關(guān)鍵的中間結(jié)果——x, y的組合分布是均勻的。

最終的表達(dá)式中，主項(xiàng)來(lái)源于數(shù)域中范數(shù)N(x+ y√(-n))的分布，利用數(shù)域的素理想定理，可以得到主項(xiàng)。

“Type I和”與“Type II和”帶來(lái)的誤差項(xiàng)，分別可以通過(guò)篩法分析和Gowers范數(shù)的均勻性假設(shè)來(lái)控制。

兩者結(jié)合后，誤差項(xiàng)對(duì)主項(xiàng)的影響是次級(jí)的。

將主項(xiàng)和誤差項(xiàng)結(jié)合，最終得出目標(biāo)公式：

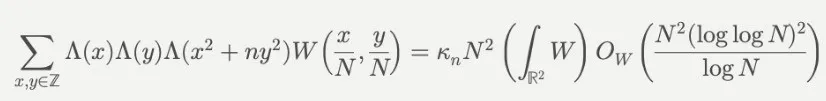
結(jié)緣于Gowers范數(shù)

這項(xiàng)研究的兩位作者——格林和索尼，說(shuō)起來(lái)也是頗有緣分。

格林是牛津大學(xué)數(shù)學(xué)教授、陶哲軒的長(zhǎng)期合作者，同時(shí)還是英國(guó)皇家學(xué)會(huì)Fellow。

索尼一開(kāi)始在賓夕法尼亞大學(xué)讀計(jì)算機(jī)，然后在2017年轉(zhuǎn)到MIT主修數(shù)學(xué)，成為了趙宇飛的學(xué)生，之后又在趙宇飛手下讀博，并于今年6月畢業(yè)。

今年初索尼成為了克萊研究員，現(xiàn)在索尼在哥倫比亞大學(xué)擔(dān)任教職。

讓兩人走到一起的，或許正是這次研究中用到的Gowers范數(shù)。

Gowers范數(shù)是1998年菲爾茲獎(jiǎng)得主、英國(guó)數(shù)學(xué)家蒂莫西·高爾斯（Timothy Gowers）在證明塞邁雷迪定理時(shí)提出的。

塞邁雷迪定理與等差數(shù)列相關(guān)：

若一個(gè)整數(shù)集A具有正的自然密度，則對(duì)任意的正整數(shù)k，都可以在A中找出一個(gè)包含k項(xiàng)的等差數(shù)列。
所謂具有正自然密度，就是當(dāng)n趨于無(wú)窮時(shí)，A與1,2,…,n這個(gè)數(shù)列的交集中元素個(gè)數(shù)與n的比值大于0。

到了2017年，陶哲軒和格林一起給出了k=4時(shí)的新上界。