在數(shù)據(jù)科學(xué)實踐中，結(jié)果的可靠性評估至關(guān)重要。準(zhǔn)確理解結(jié)果的可靠程度能夠為決策制定提供有力支持。

當(dāng)我們能夠量化結(jié)果的不確定性水平后，可以將其應(yīng)用于以下方面：

• 進(jìn)行場景規(guī)劃，評估最優(yōu)和最劣情況
• 開展風(fēng)險評估，分析對決策的影響程度
• 實施模型評估，對比不同模型的性能表現(xiàn)
• 向決策者闡述結(jié)果的可信程度

不確定性的來源分析

考慮一個具體示例：假設(shè)我們需要估算300平方米住宅的平均價格。顯然收集所有300平方米住宅的數(shù)據(jù)是不切實際的，我們只能基于具有代表性的樣本子集計算平均價格。

這就引出了不確定性的根源：采樣過程。我們僅能獲取總體的一個子集或樣本的信息。由于樣本無法完美代表整個總體，樣本估計值與真實總體參數(shù)之間必然存在偏差，這種偏差即為采樣誤差。不同的采樣方式會導(dǎo)致不同的結(jié)果。比如對同一類型住宅進(jìn)行兩次采樣，得到的平均價格可能會有所不同。

在預(yù)測平均價格時，由于無法獲取全部總體數(shù)據(jù)，只能基于總體的子集構(gòu)建模型。這導(dǎo)致了采樣不確定性的產(chǎn)生，因為無法準(zhǔn)確獲知平均價格（因變量）與面積（自變量）之間的精確關(guān)系。采樣過程必然帶來不確定性，這種不確定性需要通過科學(xué)的方法進(jìn)行量化。所以可以通過設(shè)定一個預(yù)期真值所在的區(qū)間來實現(xiàn)這一目標(biāo)。區(qū)間范圍越窄，表明估計的確定性越高（假設(shè)區(qū)間具有足夠的覆蓋率）。

在統(tǒng)計學(xué)中，量化不確定性通常使用兩個經(jīng)常被混淆的概念：置信區(qū)間和預(yù)測區(qū)間。

這兩個概念在統(tǒng)計學(xué)中具有基礎(chǔ)性地位，因此在數(shù)據(jù)科學(xué)領(lǐng)域也有廣泛應(yīng)用。從宏觀角度看，它們都為目標(biāo)變量的估計提供了概率意義上的上下界，形成了量化不確定性的區(qū)間。

從更深層次來看，這兩個概念描述的是不同的統(tǒng)計特性。因此不應(yīng)該將它們等同使用。若將置信區(qū)間誤解為預(yù)測區(qū)間，可能導(dǎo)致對不確定性的錯誤認(rèn)知，進(jìn)而影響決策的準(zhǔn)確性。

本文旨在幫助讀者理解這兩個概念的區(qū)別，將詳細(xì)討論置信區(qū)間和預(yù)測區(qū)間各自的度量對象，并據(jù)此分析它們的差異及其適用場景。讓我們首先探討使用更為廣泛的置信區(qū)間。

置信區(qū)間

置信區(qū)間用于量化從樣本集估計總體參數(shù)（如均值）時的采樣不確定性。它反映了采樣參數(shù)平均響應(yīng)的不確定性程度。

仍以房價估算為例。我們需要估計300平方米住宅的平均價格。總體包含該類別的所有住宅。由于無法獲取所有住宅的數(shù)據(jù)，只能收集部分住宅的樣本數(shù)據(jù)。

針對采集的樣本，可以通過以下公式計算樣本均值的置信區(qū)間：

其中：x 表示均值z 表示置信水平對應(yīng)的標(biāo)準(zhǔn)差倍數(shù)（95%置信水平時取1.96，99%置信水平時取2.576）s 表示樣本標(biāo)準(zhǔn)差n 表示樣本容量

這個過程可以對總體的不同樣本重復(fù)進(jìn)行。

置信區(qū)間的正確解讀

置信水平95%的實際含義是：如果重復(fù)進(jìn)行多次采樣過程，約95%的區(qū)間會包含真實的總體參數(shù)。這里的置信水平描述的是區(qū)間構(gòu)建過程的長期特性，而非針對某個具體區(qū)間的特性。這并不意味著真值有95%的概率落在某個特定樣本的區(qū)間內(nèi)。這種解釋方式體現(xiàn)了頻率學(xué)派的統(tǒng)計思想。

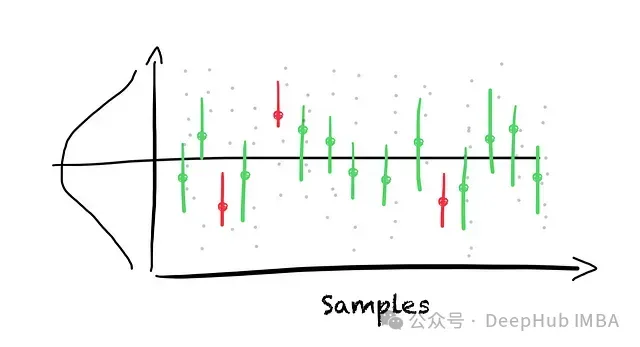
上圖展示了從正態(tài)分布中抽取不同樣本并計算90%置信區(qū)間的情況。紅色列表示不包含總體均值的置信區(qū)間。

這是一個需要仔細(xì)辨別的重要差異：95%的置信水平描述的是區(qū)間構(gòu)建過程的整體特性，而非單個具體區(qū)間的性質(zhì)。

以300平方米住宅為例，假設(shè)我們得到的95%置信區(qū)間為400,000元到1,000,000元。這意味著如果我們進(jìn)行大量重復(fù)采樣，約95%的樣本產(chǎn)生的置信區(qū)間會包含真實均值。這種表述強(qiáng)調(diào)了在重復(fù)采樣和區(qū)間計算過程中捕獲真實均值的長期概率特性。

在實際應(yīng)用中，人們常說"我們有95%的把握認(rèn)為真實總體均值位于400,000元到1,000,000元之間"。雖然這種表述并不準(zhǔn)確（因為它暗示了對特定區(qū)間的確定性），但這種表述方式更易于理解，它體現(xiàn)了95%的類似計算區(qū)間會包含真實參數(shù)這一特性。

置信區(qū)間寬度的影響因素

從前述公式可以看出，影響置信區(qū)間寬度的主要因素有兩個：總體方差和樣本容量。

總體方差越大，樣本之間的差異就越顯著。這會導(dǎo)致樣本標(biāo)準(zhǔn)差增大，進(jìn)而使置信區(qū)間變寬。這種現(xiàn)象是合理的，因為更大的變異性意味著采樣參數(shù)與總體參數(shù)的差異可能更大。

較大的樣本容量能夠降低異常值的影響，同時提高樣本的代表性。這使得估計更為可靠從而產(chǎn)生更窄的置信區(qū)間。這一點在公式中也得到了體現(xiàn)：隨著樣本容量增加，分母變大，區(qū)間寬度相應(yīng)減小。相反小樣本容量會導(dǎo)致置信區(qū)間變寬，這是因為較少的采樣提供的信息量較小，且更容易受到采樣誤差的影響。

預(yù)測區(qū)間

預(yù)測區(qū)間用于量化基于特定自變量值和歷史數(shù)據(jù)對未來單個觀測值預(yù)測的不確定性。它需要同時考慮預(yù)期值估計的不確定性和個體值的隨機(jī)波動。

如果德國300平方米住宅的95%預(yù)測區(qū)間為400,000元到1,000,000元，這表明任一300平方米住宅的實際價格有95%的概率落在該區(qū)間內(nèi)。

預(yù)測區(qū)間寬度的影響因素

預(yù)測區(qū)間的寬度主要受兩個因素影響：模型估計的方差和目標(biāo)變量的方差。與置信區(qū)間類似預(yù)測區(qū)間需要考慮模型估計的變異性。估計的方差越大，不確定性程度越高，預(yù)測區(qū)間就越寬。

預(yù)測區(qū)間還需要考慮目標(biāo)變量本身的方差。目標(biāo)變量的固有波動性越大，預(yù)測區(qū)間的寬度也會相應(yīng)增加。

在理解了這些基本概念后，我們來探討它們之間的關(guān)鍵差異。

置信區(qū)間與預(yù)測區(qū)間的核心差異

置信區(qū)間的特征

• 用于描述總體參數(shù)（如均值或回歸系數(shù)）的不確定性。（雖然"我們有95%的把握認(rèn)為總體均值落在這個范圍內(nèi)"這種表述在技術(shù)上并不嚴(yán)格準(zhǔn)確）
• 主要關(guān)注歷史數(shù)據(jù)和當(dāng)前狀態(tài)的分析

預(yù)測區(qū)間的特征

• 用于描述具體預(yù)測值的不確定性。（"我們有95%的把握認(rèn)為下一個觀測值會落在這個范圍內(nèi)"）
• 主要關(guān)注對未來狀態(tài)的預(yù)測考慮以下回歸分析模型：

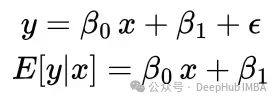
其中：y 代表目標(biāo)變量E[x|y] 代表條件期望響應(yīng)x 代表特征變量beta_0 代表斜率系數(shù)beta_1 代表截距系數(shù)epsilon 代表隨機(jī)誤差項

置信區(qū)間量化了條件期望值 E[y|x] 估計的采樣不確定性。而預(yù)測區(qū)間則反映了 y 整個取值范圍的不確定性，而不僅限于期望值。

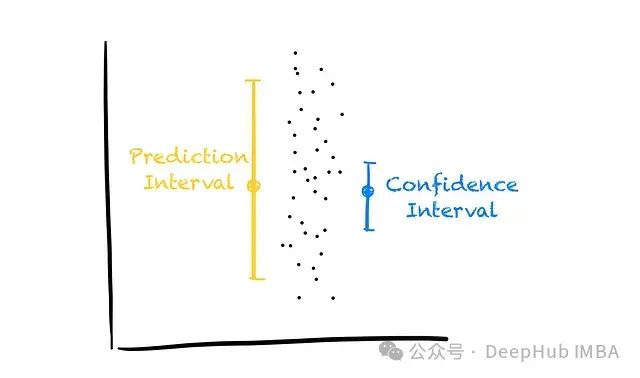
上圖示說明了置信區(qū)間與預(yù)測區(qū)間的區(qū)別：置信區(qū)間描述了給定x條件下y均值的不確定性（即 E[y|x]），而預(yù)測區(qū)間描述了給定x條件下單個y值的不確定性。

還是以房價預(yù)測的線性回歸模型為例：對于300平方米的住宅，95%置信區(qū)間可能是（250,000元，270,000元），而95%預(yù)測區(qū)間則可能是（220,000元，300,000元）。

可以觀察到預(yù)測區(qū)間明顯寬于置信區(qū)間并且這是合理的。因為預(yù)測區(qū)間不僅需要考慮均值估計的不確定性，還要包含單個觀測值的隨機(jī)變異。預(yù)測區(qū)間反映了單個300平方米住宅價格的波動范圍，而置信區(qū)間僅反映了該類住宅平均價格的估計精度。

所以如果使用置信區(qū)間來表示單個未來觀測值的不確定性，可能會導(dǎo)致對預(yù)測精度的錯誤判斷。

總結(jié)

本文深入探討了統(tǒng)計學(xué)中兩個常見但容易混淆的不確定性量化工具：置信區(qū)間和預(yù)測區(qū)間。文章通過詳細(xì)的理論分析和具體示例，闡明了這兩種區(qū)間的本質(zhì)區(qū)別：置信區(qū)間用于量化總體參數(shù)（如均值）估計的不確定性，主要反映采樣過程帶來的統(tǒng)計不確定性；而預(yù)測區(qū)間則用于量化單個未來觀測值的不確定性，需要同時考慮模型估計和隨機(jī)變異的雙重影響。

這種區(qū)別直接導(dǎo)致了預(yù)測區(qū)間通常比置信區(qū)間更寬。理解這兩種區(qū)間的差異對于正確評估和解釋數(shù)據(jù)分析結(jié)果至關(guān)重要，能夠幫助數(shù)據(jù)科學(xué)從業(yè)者在實踐中做出更準(zhǔn)確的判斷和決策。通過準(zhǔn)確理解和恰當(dāng)使用這兩種統(tǒng)計工具，我們能夠更好地量化和傳達(dá)分析結(jié)果中的不確定性，從而提供更可靠的數(shù)據(jù)支持。