大模型做奧賽題游刃有余，簡(jiǎn)單的數(shù)數(shù)卻屢屢翻車(chē)的原因找到了。

谷歌的一項(xiàng)新研究，發(fā)現(xiàn)大模型不會(huì)數(shù)數(shù)的原因，并不是簡(jiǎn)單的tokenizer所致，而是沒(méi)有足夠的空間來(lái)存儲(chǔ)用于計(jì)數(shù)的向量。

數(shù)出一段話中某個(gè)單詞出現(xiàn)的次數(shù)，這樣簡(jiǎn)單的任務(wù)可以難倒許多大模型，GPT-4o、Claude 3.5也無(wú)法幸免。

如果再進(jìn)一步，想要找到出現(xiàn)頻率最高的一個(gè)詞，更是難如登天，即便能蒙對(duì)給出的具體數(shù)量也是錯(cuò)的。

有人認(rèn)為是詞匯的token化導(dǎo)致了大模型看到的“詞”和我們的看法不一致，但論文表明，實(shí)際情況并不是這么簡(jiǎn)單。

想數(shù)清單詞，嵌入維度要夠大

Transformer的計(jì)數(shù)能力與其嵌入維度d和詞匯量m（指詞匯表中詞的數(shù)量，非序列長(zhǎng)度）的關(guān)系密切相關(guān)。

詳細(xì)的原因，就涉及到了Transformer統(tǒng)計(jì)詞頻時(shí)的機(jī)制。

Transformer通過(guò)一種特殊的嵌入方式，利用嵌入空間的線性結(jié)構(gòu)，巧妙地將計(jì)數(shù)問(wèn)題轉(zhuǎn)化為了向量加法。

具體說(shuō)是將每個(gè)詞映射到一個(gè)獨(dú)特的正交向量上，在這種表示下，詞頻可以通過(guò)對(duì)這些正交向量求和來(lái)簡(jiǎn)單地計(jì)算。

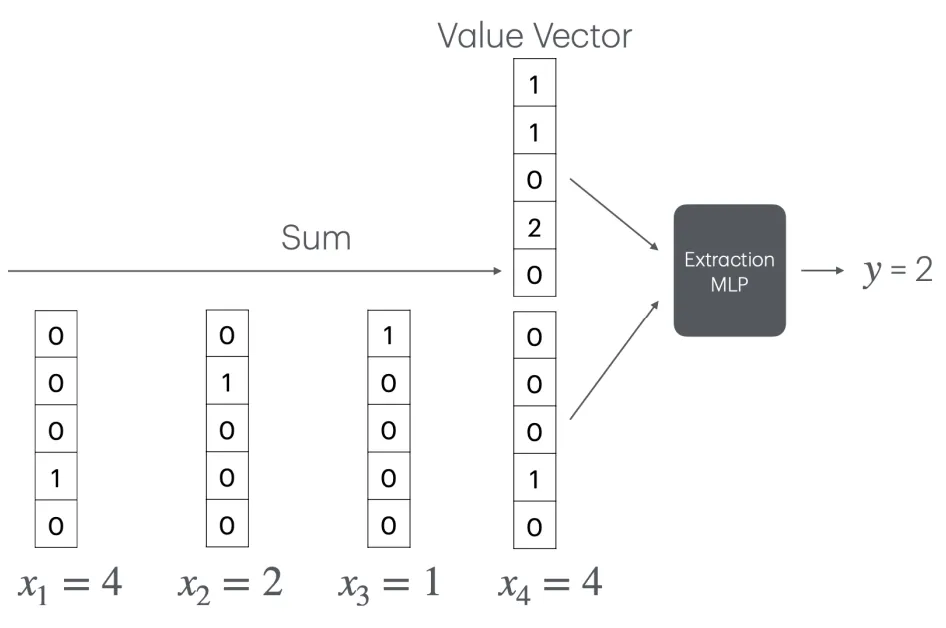
然而，這種機(jī)制的局限性在于，它要求詞匯表中的每個(gè)詞都有一個(gè)獨(dú)立的正交向量表示，因此嵌入維度必須大于詞匯量。

嵌入維度不足時(shí)，詞向量就無(wú)法保持正交性，詞頻的線性疊加也就無(wú)法實(shí)現(xiàn)了。

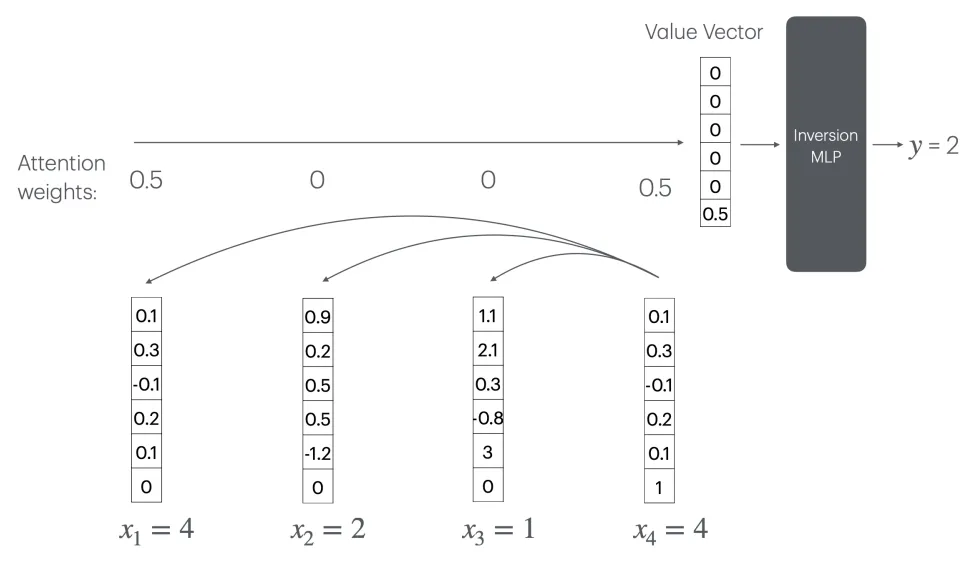
此時(shí)Transformer要實(shí)現(xiàn)計(jì)數(shù)，可以通過(guò)注意力機(jī)制（CountAttend）來(lái)實(shí)現(xiàn)，但需要一個(gè)隨序列長(zhǎng)度n線性增長(zhǎng)的大型“逆轉(zhuǎn)MLP”層。

具體來(lái)說(shuō)，模型首先通過(guò)注意力賦予被查詢?cè)~較大的權(quán)重，再利用位置編碼將注意力權(quán)重提取到值向量的最后一個(gè)元素，這個(gè)元素實(shí)際記錄了被查詢?cè)~的出現(xiàn)頻率的倒數(shù)。

這意味著，模型需要一個(gè)大小為O(n)的MLP層來(lái)計(jì)算1/x函數(shù)（x為某個(gè)詞出現(xiàn)的次數(shù)）。

但進(jìn)一步分析表明，任何常數(shù)層ReLU網(wǎng)絡(luò)都無(wú)法在o(n)的神經(jīng)元數(shù)量下逼近1/x函數(shù)。

因此，對(duì)于固定規(guī)模的Transformer，這種方案無(wú)法推廣到任意長(zhǎng)度的序列。當(dāng)序列長(zhǎng)度超出訓(xùn)練集長(zhǎng)度時(shí)，模型的計(jì)數(shù)能力會(huì)急劇惡化。

長(zhǎng)度非主要因素，詞匯表中數(shù)量是關(guān)鍵

為了驗(yàn)證這一結(jié)論，作者一共進(jìn)行了兩個(gè)實(shí)驗(yàn)。

第一個(gè)實(shí)驗(yàn)，是在一個(gè)從頭開(kāi)始訓(xùn)練的Transformer模型上進(jìn)行的，具體有關(guān)參數(shù)如下：

• 使用一個(gè)由兩個(gè)Transformer層、四個(gè)注意力頭組成的標(biāo)準(zhǔn)模型；
• 嵌入維度d的取值范圍為8到128；
• 對(duì)每個(gè)固定的d，詞匯量m從5到150變化，分別測(cè)試20個(gè)不同的值；
• 模型使用Adam優(yōu)化器從零開(kāi)始訓(xùn)練，批量大小為16，學(xué)習(xí)率為10^-4，訓(xùn)練10萬(wàn)步。

訓(xùn)練和評(píng)測(cè)數(shù)據(jù)通過(guò)隨機(jī)采樣生成。首先從大小為m的詞匯表中均勻采樣n個(gè)詞，構(gòu)成一個(gè)長(zhǎng)度為n的序列。

序列長(zhǎng)度n設(shè)置為n=10m，平均每個(gè)詞出現(xiàn)的次數(shù)固定為10次，一共使用了1600個(gè)樣本進(jìn)行測(cè)試。

作者發(fā)現(xiàn)，隨著詞匯量的增加，模型的計(jì)數(shù)準(zhǔn)確率呈階梯狀下降，臨界點(diǎn)恰好出現(xiàn)在詞匯量超過(guò)嵌入維度的時(shí)刻。

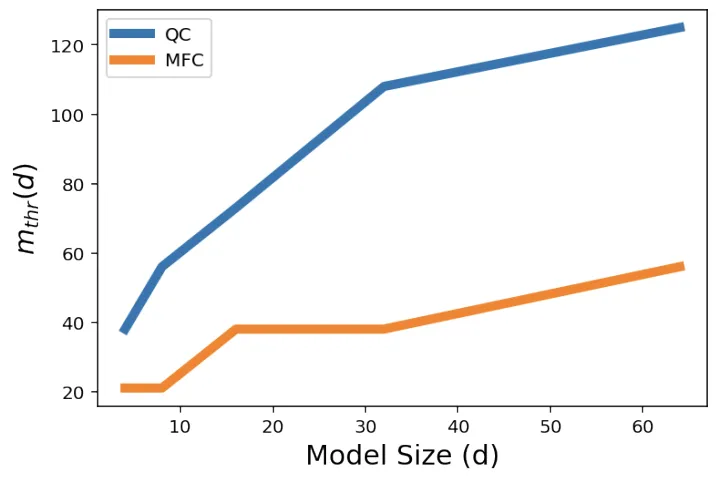
為了進(jìn)一步量化模型的計(jì)數(shù)能力，作者定義了一個(gè)指標(biāo)m_thr，表示模型的計(jì)數(shù)準(zhǔn)確率下降到80%時(shí)的臨界詞匯量。

直觀地說(shuō)，m_thr反映了在給定嵌入維度下，模型可以“承受”的最大詞匯量，m_thr越大說(shuō)明模型的計(jì)數(shù)能力越強(qiáng)。

結(jié)果顯示，對(duì)于計(jì)數(shù)（QC）和找出最高頻詞（MFC）的任務(wù)，m_thr都隨嵌入維度d的增大而近似線性增長(zhǎng)。

第二個(gè)實(shí)驗(yàn)則是在預(yù)訓(xùn)練的Gemini 1.5模型上開(kāi)展，在這個(gè)實(shí)驗(yàn)中，作者更關(guān)注詞匯量對(duì)計(jì)數(shù)能力的影響。

他們?cè)O(shè)計(jì)了一系列計(jì)數(shù)任務(wù)，每個(gè)任務(wù)使用不同大小的詞匯表，并把每個(gè)詞在序列中出現(xiàn)的平均次數(shù)固定。

這意味著，在實(shí)驗(yàn)組當(dāng)中，詞匯量越大，序列長(zhǎng)度也就越長(zhǎng)。

作為對(duì)照，作者還設(shè)置了一個(gè)“Binary Baseline”，詞匯表中只有固定為兩個(gè)詞，但序列長(zhǎng)度與主實(shí)驗(yàn)組相同。

這樣一來(lái)，就可以判斷出帶來(lái)模型計(jì)數(shù)誤差的究竟是詞匯量還是序列長(zhǎng)度。

實(shí)驗(yàn)結(jié)果顯示，隨著詞匯量的增加，Gemini 1.5在計(jì)數(shù)任務(wù)上的平均絕對(duì)誤差顯著上升，而“Binary Baseline”的誤差要低得多。

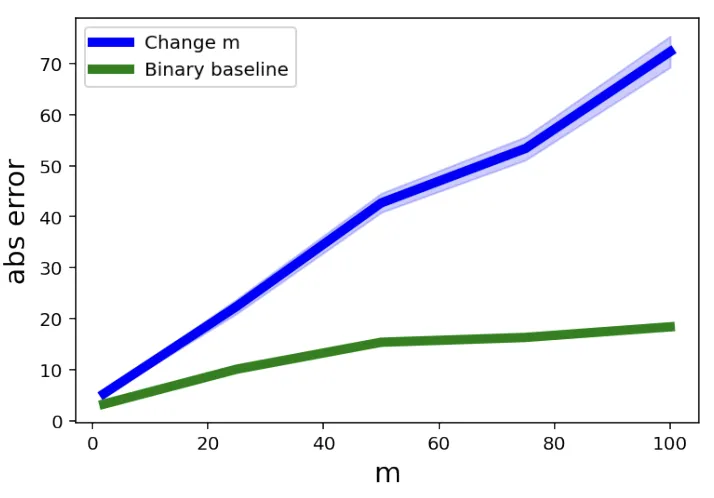
這表明，詞匯量的增加，而非序列長(zhǎng)度的增長(zhǎng)，是導(dǎo)致大模型計(jì)數(shù)能力下降的主要原因。

不過(guò)作者也表示，雖然這項(xiàng)研究一定程度上劃定了大模型計(jì)數(shù)能力的上下界，但這些界限還不夠緊致，距離理想的結(jié)果還有一定差距。

同時(shí)，作者也沒(méi)有探究增加Transformer的層數(shù)是否會(huì)改變這一結(jié)論，需要未來(lái)開(kāi)發(fā)新的技術(shù)工具才能進(jìn)一步驗(yàn)證。

論文地址：https://arxiv.org/abs/2407.15160