向大模型輸入「Michael Jordan plays the sport of _____（邁克爾?喬丹從事的體育運動是……）」，然后讓其預測接下來的文本，那么大模型多半能正確預測接下來是「basketball（籃球）」。

這說明在其數(shù)以億計的參數(shù)中潛藏了有關(guān)這個特定個人的相關(guān)知識。用戶甚至會感覺這些模型記憶了大量事實。

但事實究竟如何呢？

近日，3Blue1Brown 的《深度學習》課程第 7 課更新了，其中通過生動詳實的動畫展示了 LLM 存儲事實的方式。視頻瀏覽量高達 18 萬次。

去年 12 月，谷歌 DeepMind 的一些研究者發(fā)布了一篇相關(guān)論文，其中的具體案例便是匹配運動員以及他們各自的運動項目。

雖然這篇論文并未完全解答有關(guān) LLM 事實存儲的問題，但也得到了一些頗為有趣的結(jié)果，其中的一個重點是：事實保存在網(wǎng)絡(luò)中的一個特定部分，這個部分也就是我們熟知的多層感知器（MLP）。

在 3Blue1Brown 剛剛更新的這期視頻中，他們用 23 分的視頻演示了大型語言模型如何存儲和處理信息，主要包括以下部分：

• LLM 中隱藏的事實是什么
• 快速回顧 Transformers
• 示例
• 多層感知器
• 計算參數(shù)

視頻地址：https://www.youtube.com/watch?v=9-Jl0dxWQs8

在演示視頻中，3b1b 的作者口齒清晰、語言標準，配合著高清畫面，讓讀者很好地理解了 LLM 是如何存儲知識的。

很多用戶在看完視頻后，都驚訝于 3Blue1Brown 教學質(zhì)量：

還有網(wǎng)友表示，坐等更新這期視頻已經(jīng)很久了：

接下來我們就深入 MLP 的細節(jié)吧。在這篇文章中，機器之心簡要介紹了核心內(nèi)容，感興趣的讀者可以通過原視頻查看完整內(nèi)容。

MLP 在大模型中的占比不小，但其實結(jié)構(gòu)相比于注意力機制這些要簡單許多。盡管如此，理解它也還是有些難度。

為了簡單，下面繼續(xù)通過「喬丹打籃球」這個具體示例進行說明吧。

首先，我們先簡單了解一下 Transformer 的工作流程。Transformer 的訓練目標是基于已有 token 預測下一個 token（通常表示詞或詞組），而每個 token 都關(guān)聯(lián)了一個高維向量。

這些向量會反復通過兩類運算：注意力（允許向量之間彼此傳遞信息）與多層感知器（MLP）。當然，它們之間還存在一個特定的歸一化步驟。

在向量經(jīng)過多次如此迭代之后，我們希望每個向量都已經(jīng)吸收了足夠多的信息。這些信息有的來自訓練模型時植入模型權(quán)重的一般性知識，也有的來自上下文。這些知識就是模型預測下一 token 的依據(jù)。

需要注意的是，這些向量編碼的并不僅僅是單個詞匯，而是會在信息在網(wǎng)絡(luò)中流動時根據(jù)周圍的環(huán)境和模型的知識吸收更加豐富的含義。

總之，每一個向量編碼的信息都遠遠超過了單個詞匯的含義，如此模型才能預測接下是什么。而存儲這些信息就是 MLP（注意力的作用是將上下文結(jié)合在一起），也因此大模型的大多數(shù)參數(shù)都在 MLP 中（約三分之二）。

繼續(xù)「喬丹打籃球」這個示例。MLP 是如何存儲這一事實的。

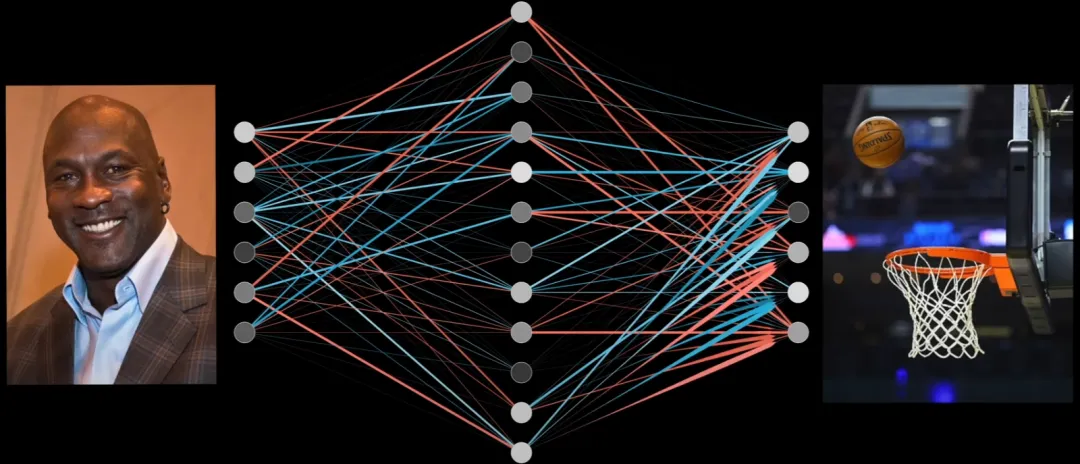
首先我們做一些假設(shè)：在高維空間中有這樣三個不同的向量，它們分別定義了喬丹的姓 Jordan 和名 Michael 以及籃球 Basketball。

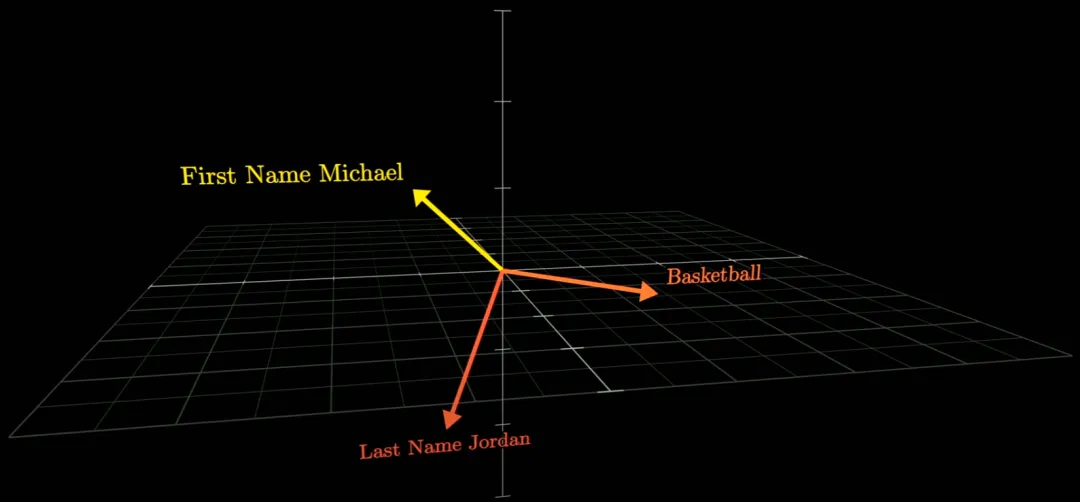
現(xiàn)在，如果該空間中有一個向量與 Michael 向量的乘積為 1，則我們認為該向量編碼了 Michael 這一概念；而如果這個乘積為 0 甚至負數(shù)，則認為該向量與 Michael 沒有關(guān)聯(lián)。

同樣，我們可以計算該向量與 Jordan 或 Basketball 的乘積，以了解其與這兩個概念的關(guān)聯(lián)程度。

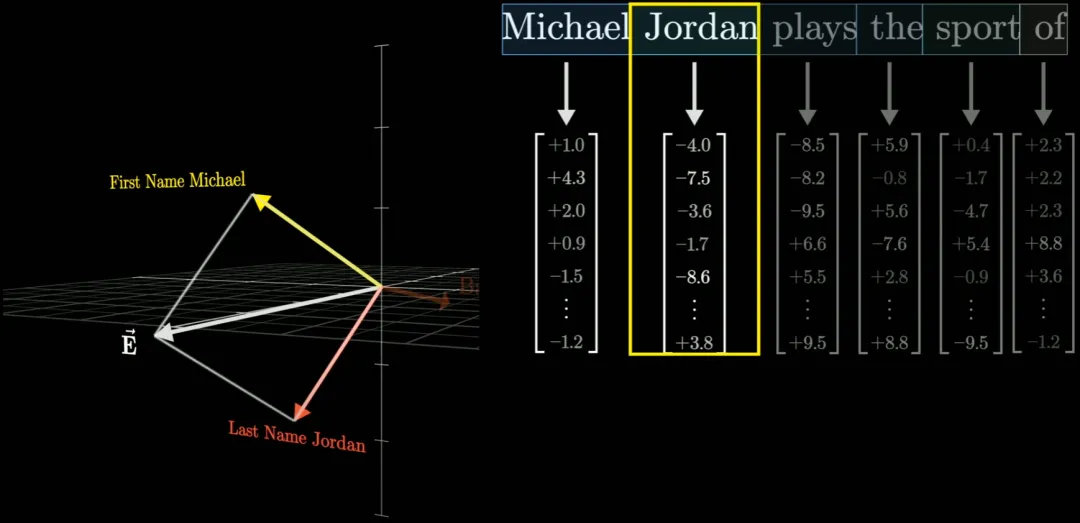
而通過訓練，可讓該向量與 Michael 和 Jordan 的乘積均為 1，此時就可以認為該向量編碼了 Michael Jordan 這個整體概念。

MLP 的內(nèi)部細節(jié)

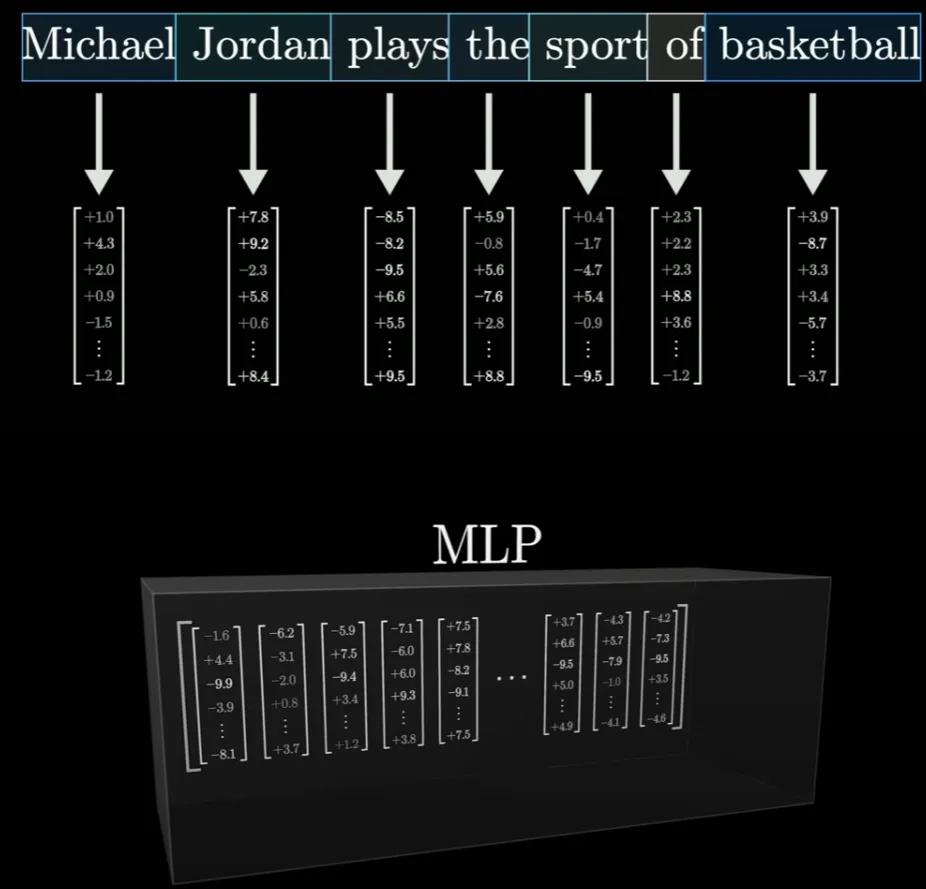
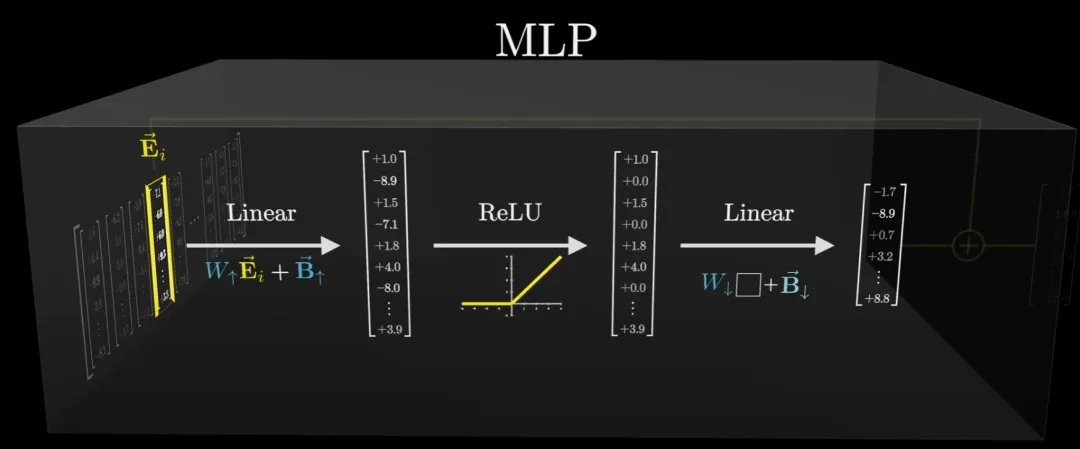
當這個編碼了上述文本的向量序列穿過一個 MLP 模塊時，該序列中的每個向量都會經(jīng)歷一系列運算：

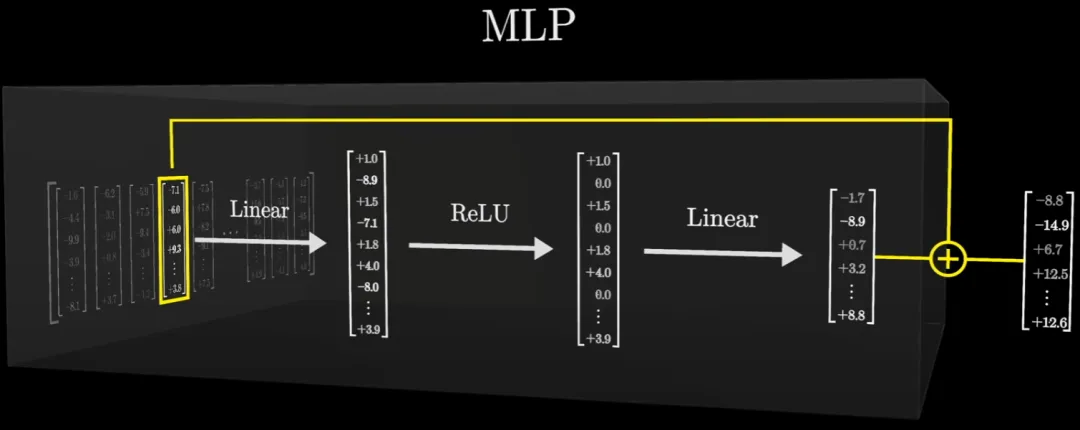
之后，會得到一個與輸入向量同維度的向量。然后再將所得向量與輸入向量相加，得到輸出向量。

序列中的每個向量都會經(jīng)歷這樣的操作，此時這些操作都是并行執(zhí)行的，彼此之間互不影響。

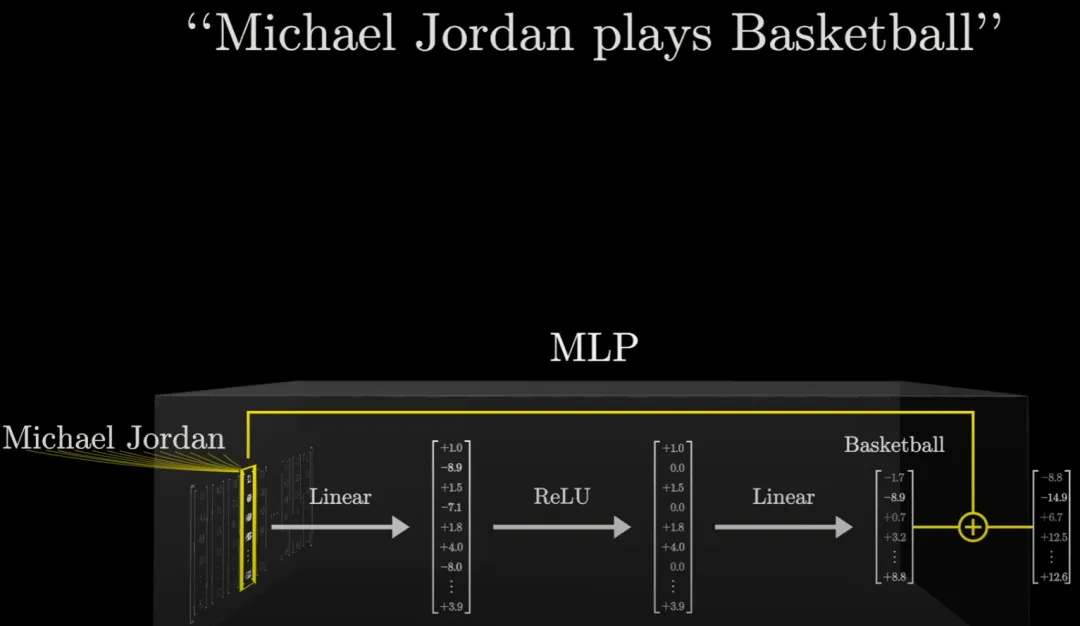
對于「喬丹打籃球」，我們希望對于輸入的「Michael Jordan」，經(jīng)過一系列運算之后，能得到「Basketball」的向量。

首先來看這個過程的第一步。這個線性投射過程就相當于讓輸入向量乘以一個大型矩陣。這個矩陣里面的數(shù)據(jù)就是所謂的模型參數(shù)（model parameter）。你可以將其視為一個布滿控制旋鈕的儀表盤 —— 通過調(diào)整這些參數(shù)，我們就能控制模型的行為。

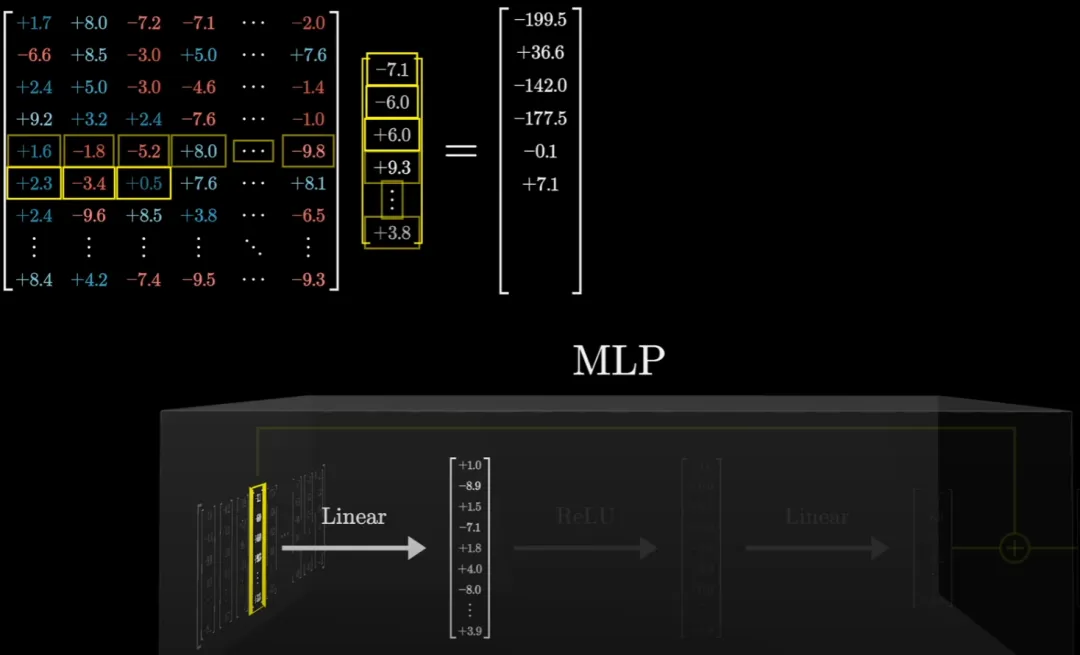
對于矩陣乘法，視頻中分享了一個視角。我們可以將矩陣乘法看作是將矩陣的每一行都視為一個向量，然后將這些行與被處理的向量（這里用 E 表示，意為 embeding，即嵌入）進行一系列點乘。

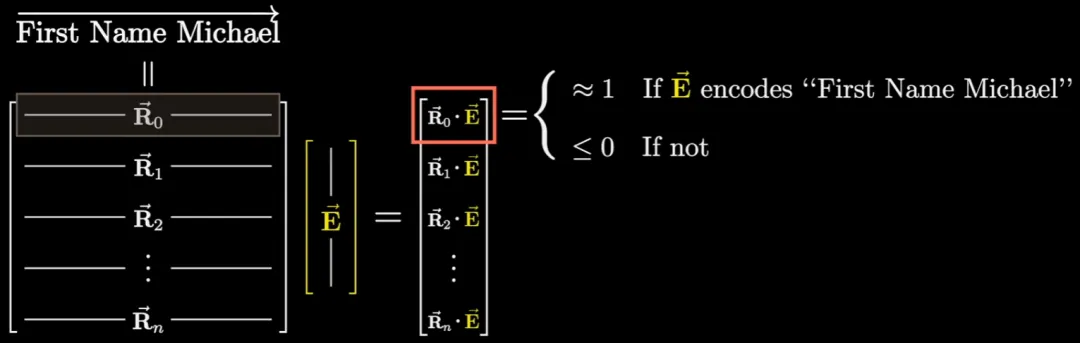
如果我們假設(shè)該矩陣的第一行剛好編碼了「First Name Michael」且被處理向量也編碼了它，那么所得的點積就約為 1。

而如果它們同時編碼了姓和名，那么所得的結(jié)果應該約等于 2。

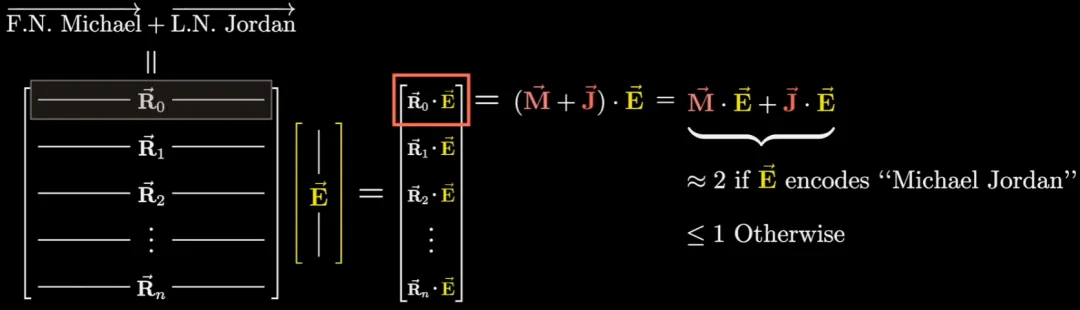
你可以認為該矩陣的其它行正在并行地處理其它問題。

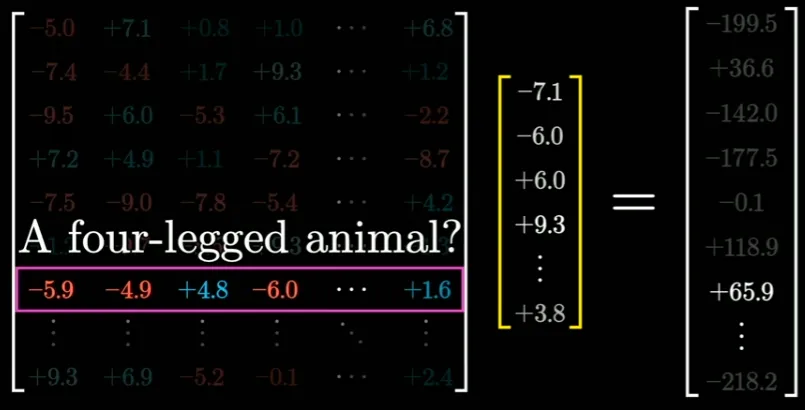
另外，通常來說，這一步還會向輸出添加另一個向量，也就是所謂的偏置向量，其中的參數(shù)是從數(shù)據(jù)中學習得到的。

在這個例子中，我們可以看到這個偏置向量的第一個元素為 -1。也就是說在最終的輸出向量中，之前得到的相關(guān)點積減去了 1。為什么要這樣操作？這是因為這樣一來，當且僅當向量編碼了全名「Michael Jordan」時，所得向量的第一項為正數(shù)，否則就為 0 或負數(shù)。

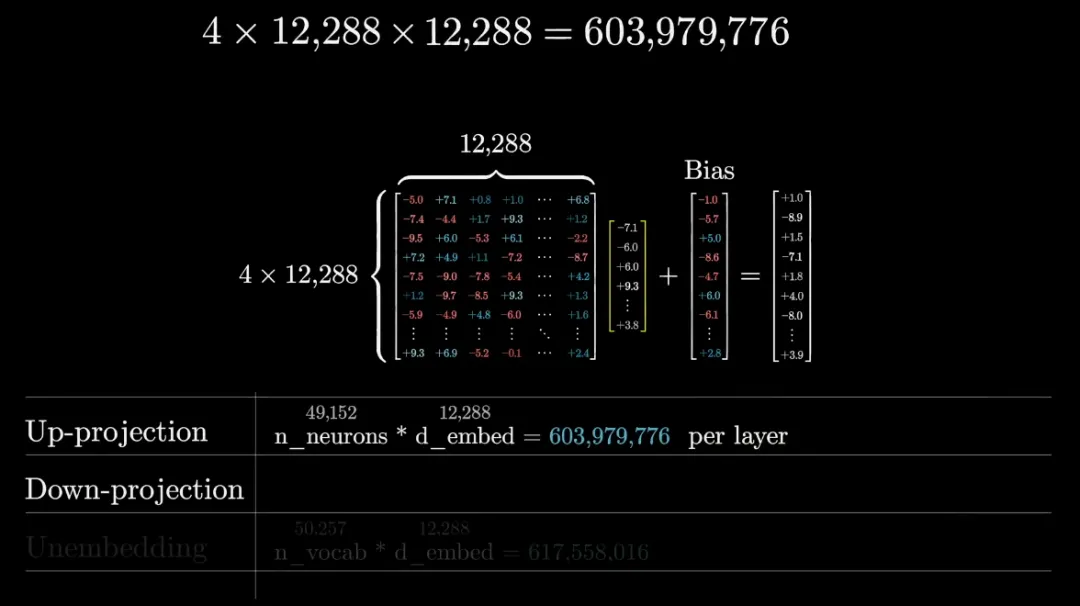
在實踐中，模型矩陣的規(guī)模非常大，比如 GPT-3 的矩陣有 49152 行和 12288 列（這個列數(shù)就是嵌入空間維度）。

事實上，這個行數(shù)恰好是嵌入空間維數(shù)的四倍。其實這只是一種設(shè)計選擇，你可以讓它更多，也可以讓它更少。

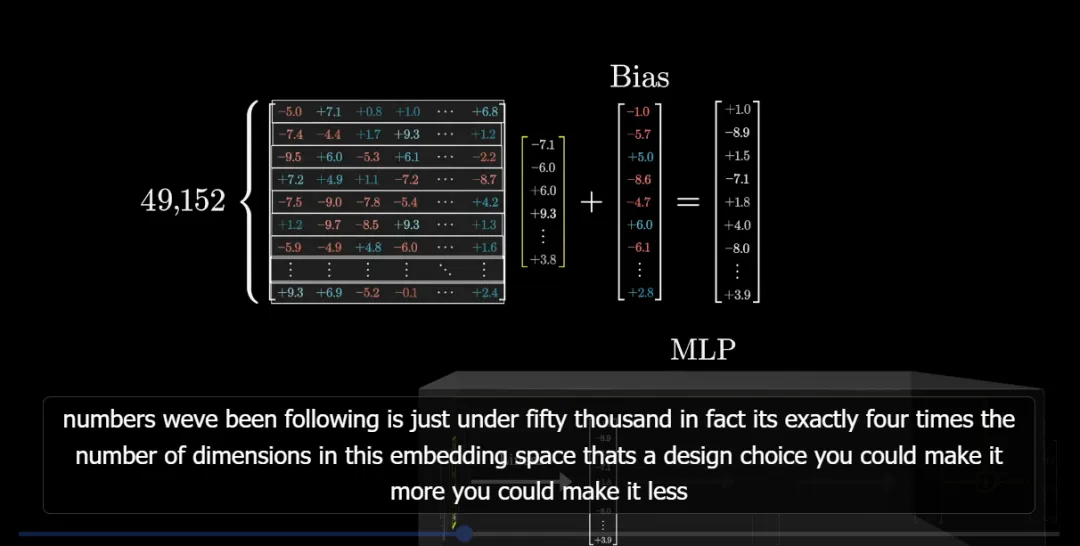
接下來我們用更簡潔的方式表示這個矩陣和向量，如下動圖所示：

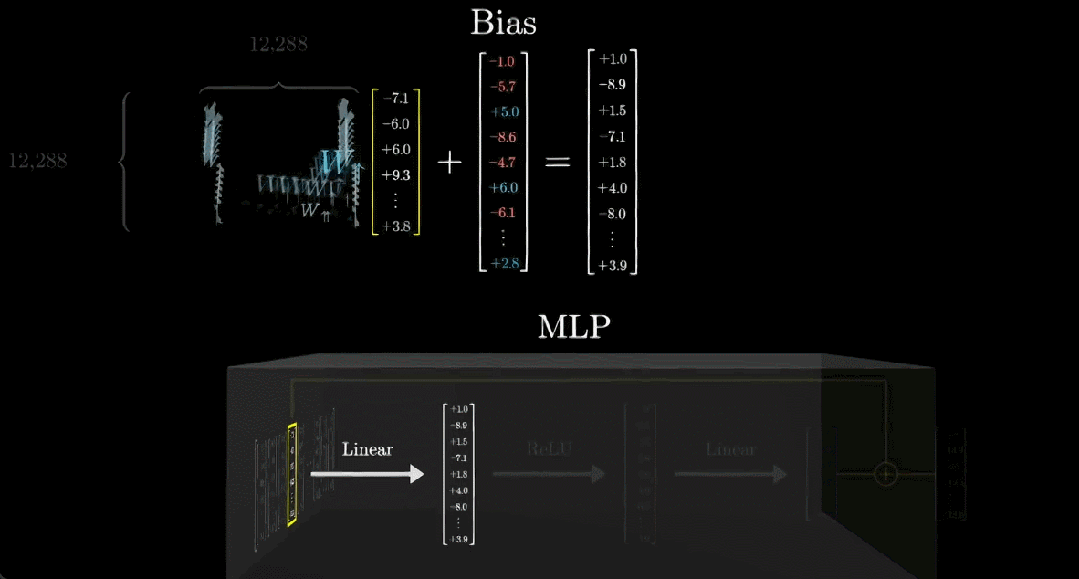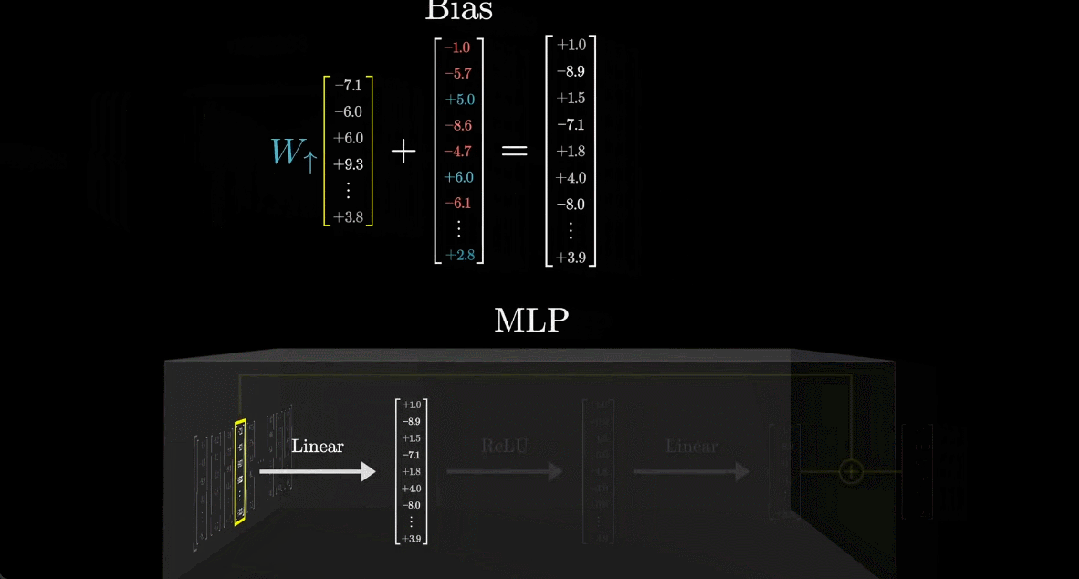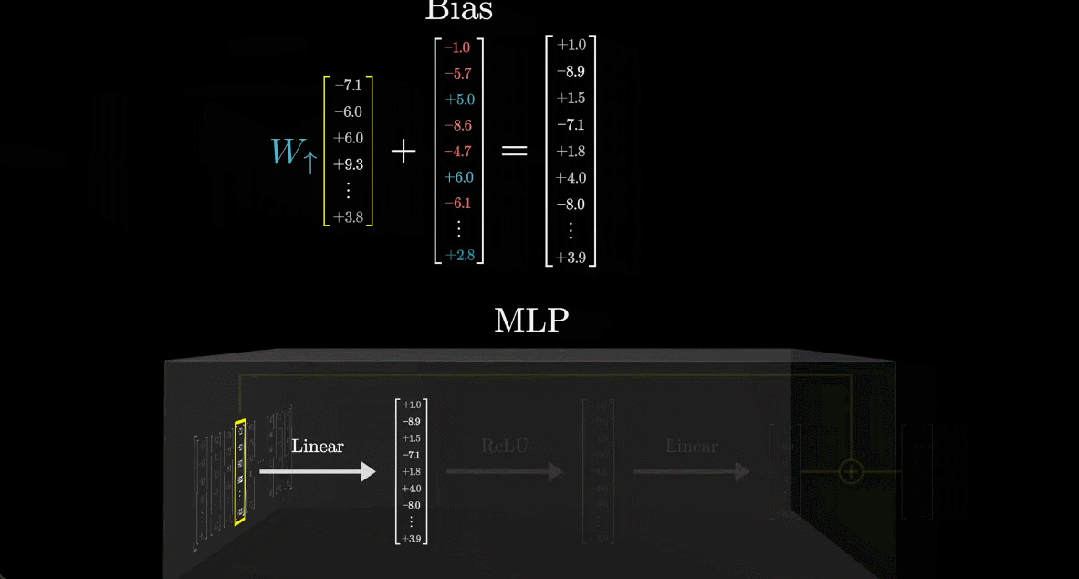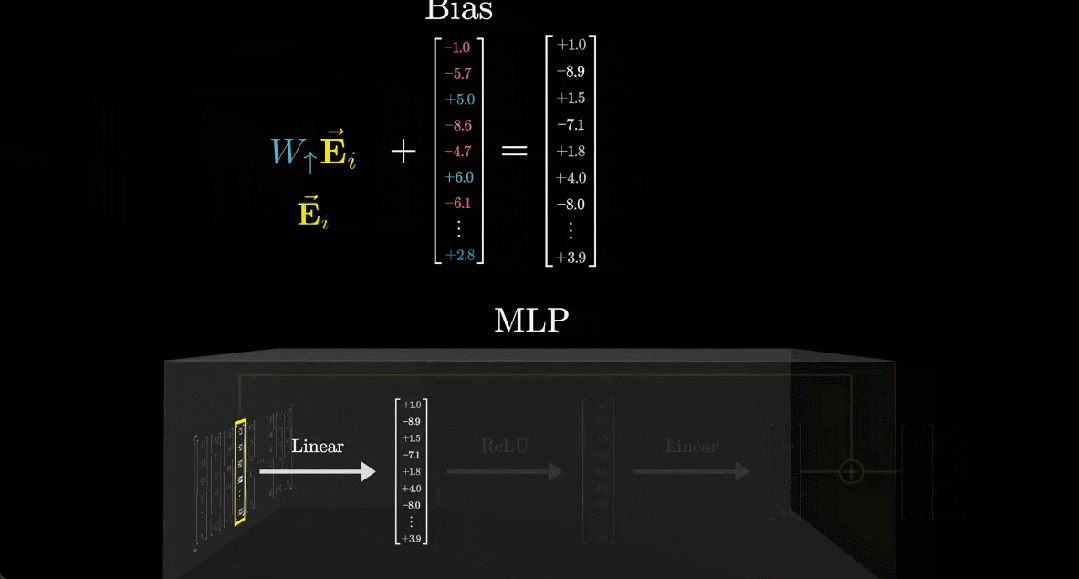
經(jīng)過上述線性過程之后，需要對輸出向量進行整理。這里通常會用到一個非常簡單的函數(shù)：整流線性單元（ReLU）。

深度學習社區(qū)傳統(tǒng)上喜歡使用過于花哨的名字，這個非常簡單的函數(shù)通常被稱為整流線性單元（ReLU）。

繼續(xù)我們的例子，中間向量的第一個元素在當且僅當全名是 Michael Jordan 時才為 1，否則為零或負數(shù)，在將其通過 ReLU 后，會得到一個非常干凈的值，其中所有零和負值都被截斷為零。因此對于全名 Michael Jordan，該輸出為 1，否則為 0。這個行為和「與門」非常相似。另外 ReLU 還有一個相對平滑的版本 GeLU。

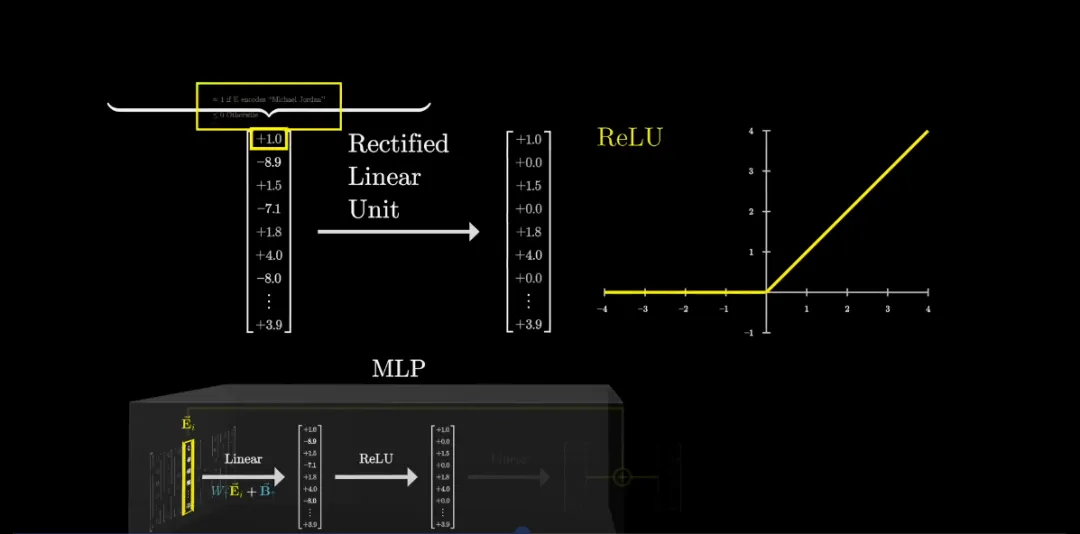
接下來又是一個線性投射步驟，這一步與第一步非常相似：乘以一個大型矩陣，加上偏置，得到輸出向量。

但這一次，對于這個大型矩陣，我們不再以行的思路來思考它，而是以列的思路來看。這些列的維度與向量空間一樣。

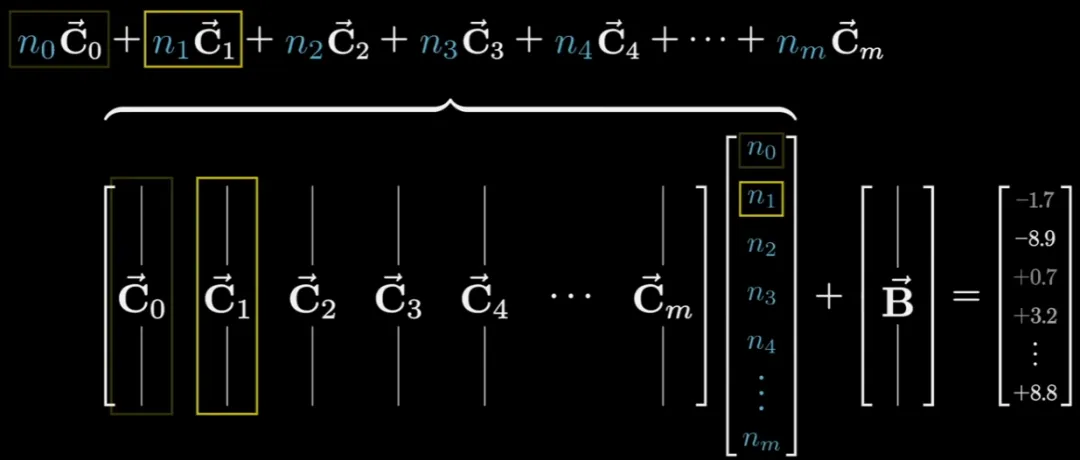
如果第一列表示的是「Basketball」且 n_0 為 1（表示該神經(jīng)元已激活），則該結(jié)果就會被添加到最終結(jié)果中；否則就不會影響最終結(jié)果。當然，這些列也可以表示任何概念。

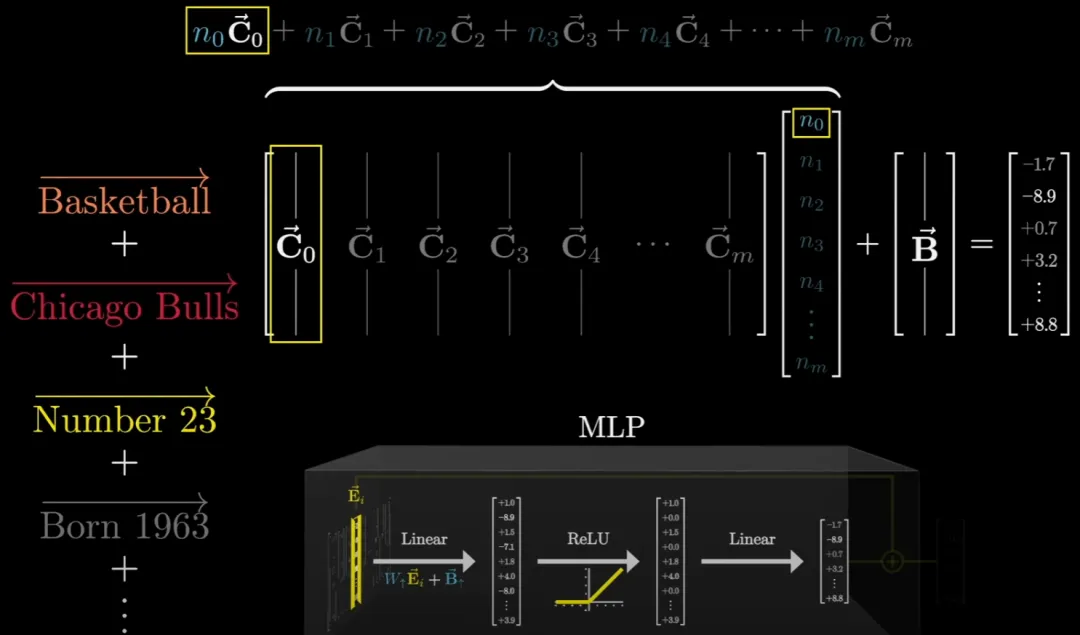
類似地，我們將這個大矩陣簡化表示為 W ↓，將偏置表示為 B↓，并將其放回到圖中。

舉例來說，如果輸入向量中同時編碼了名字 Michael 和姓氏 Jordan，那么觸發(fā)操作序列后，便會得到指向 Baskerball 方向的輸出向量。

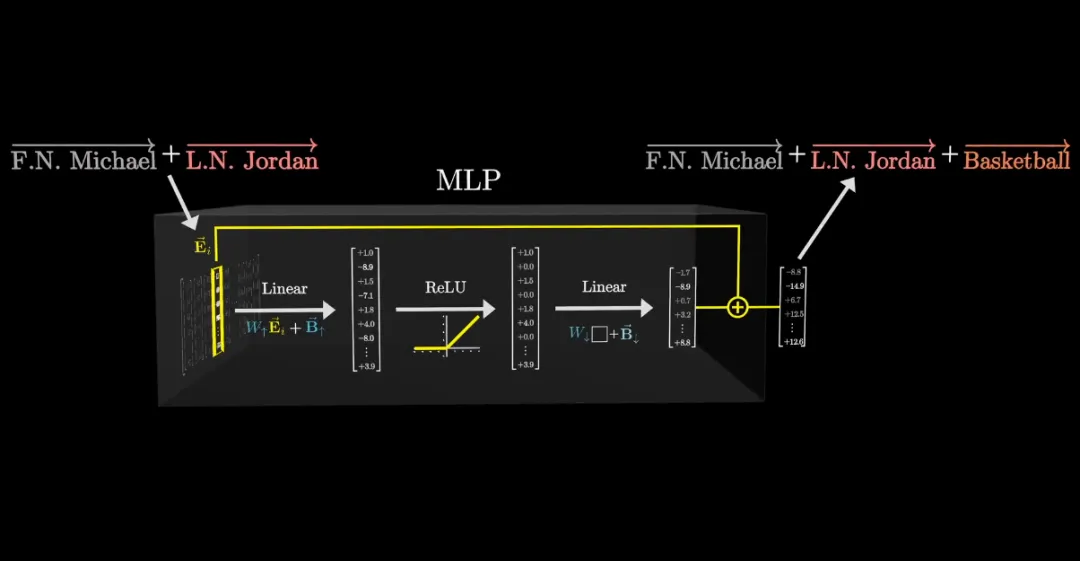
這個過程會并行地針對所有向量執(zhí)行

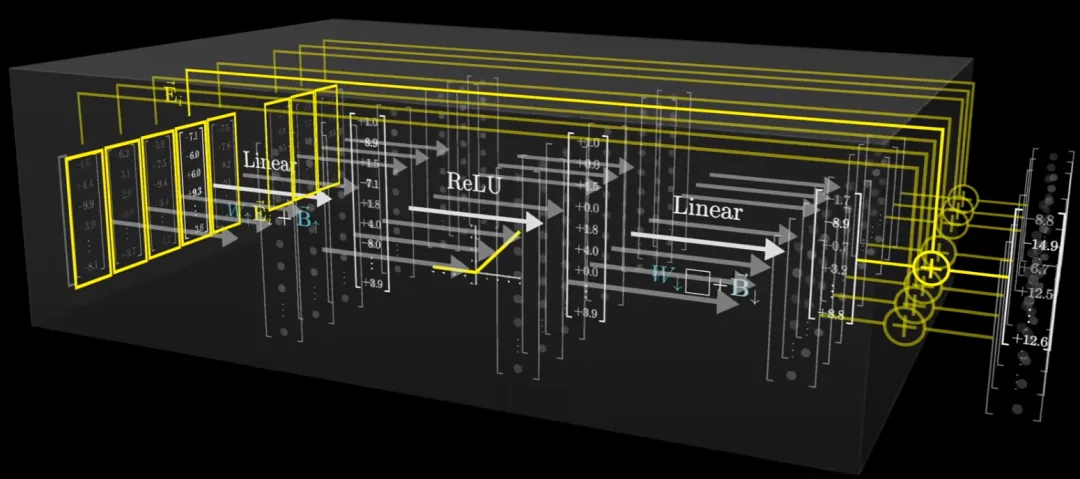
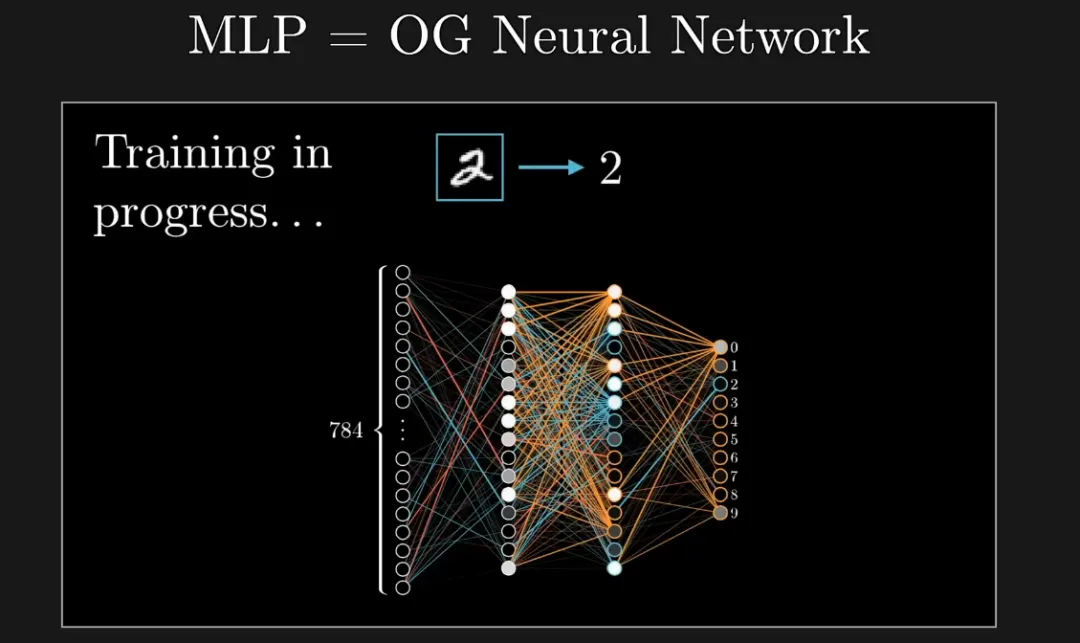
這就是 MLP 的運算過程：兩個矩陣乘積，每個都添加了偏置。此前這種網(wǎng)絡(luò)曾被用來識別手寫數(shù)字，效果還算不錯。

GPT-3 中有 1750 億參數(shù)是如何計算的？

在接下來的章節(jié)中，作者介紹了如何計算 GPT-3 中的參數(shù)，并了解它們的位置。

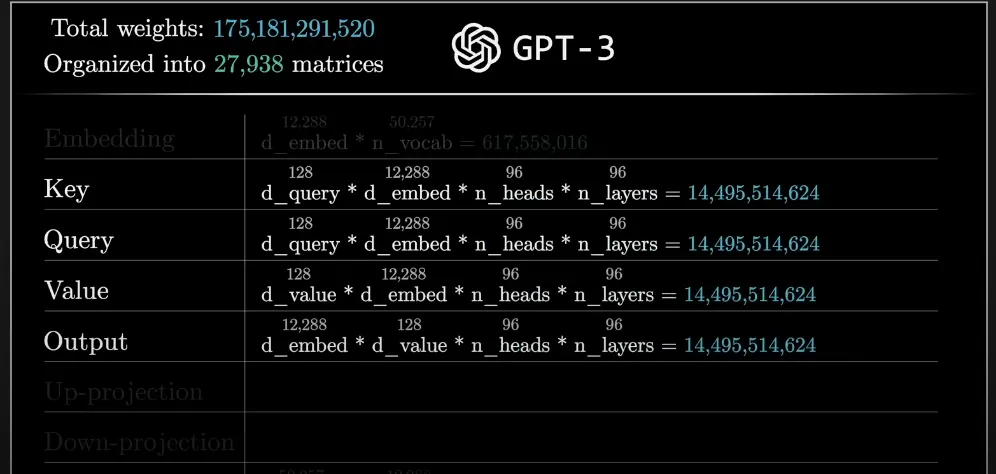
對于 GPT-3 來說，嵌入空間的大小是 12288，將它們相乘，僅該矩陣就有六億多個參數(shù)，而向下投影（第二個矩陣）具有相同數(shù)量的參數(shù)，只是形狀進行了轉(zhuǎn)置，所以它們加起來大約有十二億參數(shù)。

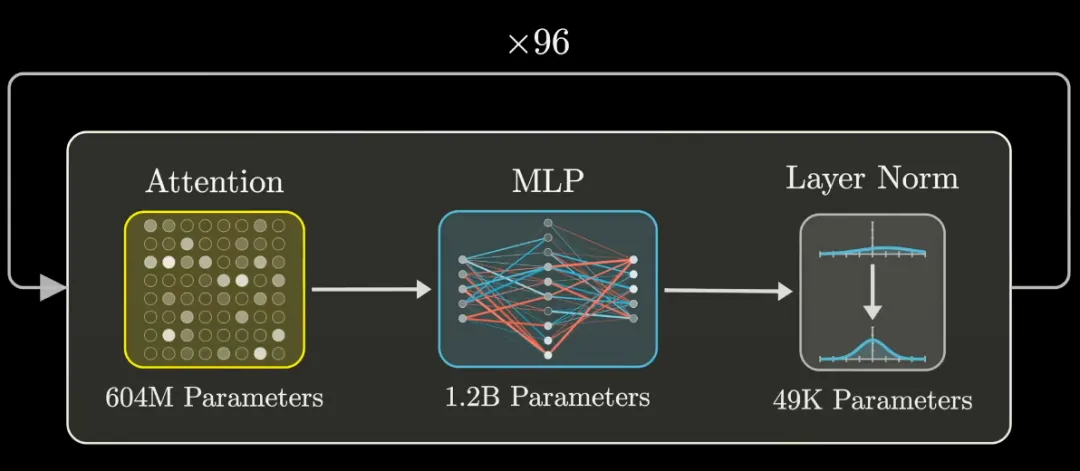
此外，作者表示還需要考慮另外幾個參數(shù)，但這只占總數(shù)的很小一部分，可忽略不計。嵌入向量序列流經(jīng)的不是一個 MLP，而是 96 個不同的 MLP，因此用于所有這些塊的參數(shù)高達 1000 多億，這約占網(wǎng)絡(luò)中總參數(shù)的三分之二。

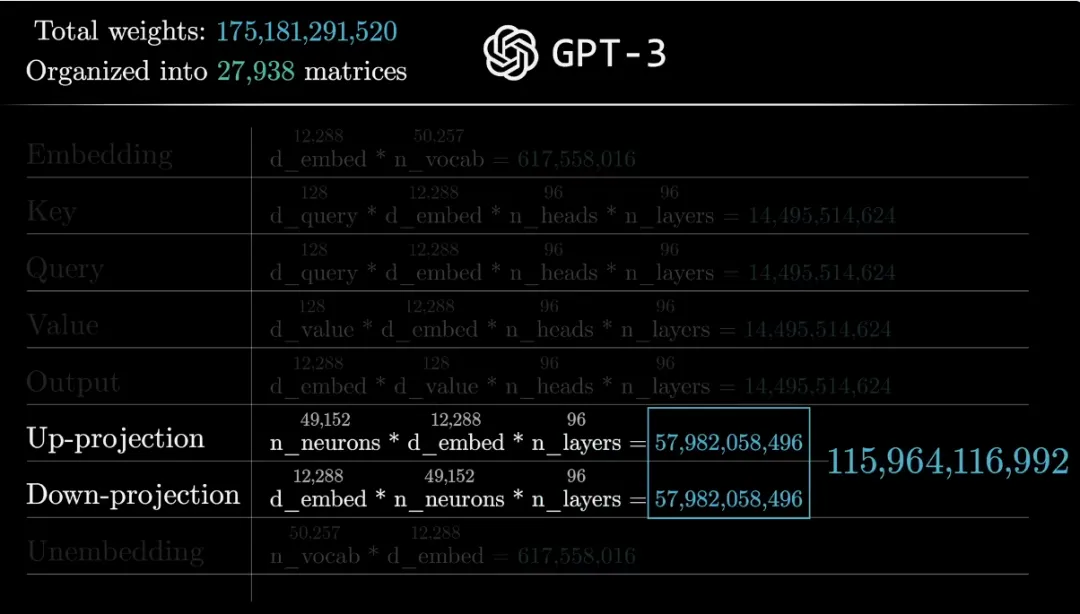
最后，將注意力塊、嵌入和 unembedding 等組件的所有參數(shù)加起來，總計可以得到 1750 億參數(shù)。

另外值得一提的是，還有另一組與歸一化步驟相關(guān)的參數(shù)，不過視頻示例中跳過了這些參數(shù)，它們只占總數(shù)的很小一部分。

視頻最后介紹了疊加（Superposition）這一概念。證據(jù)表明，單個神經(jīng)元很少像邁克爾?喬丹那樣代表某個單一特征，實際上可能有一個很好的理由，這與目前在可解釋性研究人員中流傳的一個想法有關(guān)，稱為 Superposition，這是一個假設(shè)，可能有助于解釋為什么這些模型特別難以解釋，以及為什么它們的擴展性出奇地好。

感興趣的讀者可以參考原視頻，了解更多內(nèi)容。

3blue1brown 介紹

3blue1brown 是一個專門制作可視化講解視頻的頻道，其內(nèi)容覆蓋數(shù)學、人工智能等領(lǐng)域，每門課都配有直觀生動的動畫演示，幫助觀眾加深對概念定理的理解。

除了 YouTube 上 640 萬訂閱者之外，3b1b 在 B 站上還有官方賬號，粉絲數(shù)量超過 215 萬，每個視頻都是 10 萬以上播放量，甚至有老師在課堂上播放該頻道的視頻。對于一個硬核教學 UP 主來說，這樣的成績幾乎是無人可及了。

作為一直以來都十分受歡迎的理解數(shù)學概念的網(wǎng)站，3blue1brown 的可視化一直都做得非常好。在本期視頻中，我們可以直觀感受到了。

3b1b 的創(chuàng)立者 Grant Sanderson，畢業(yè)于斯坦福大學數(shù)學系，他的大部分視頻和動畫引擎是獨立完成的，這是他此前在斯坦福學習時的業(yè)余項目。

在斯坦福，Grant「走了點計算機科學的彎路」，隨后畢業(yè)加入了 Khan Academy 并擔任了兩年的數(shù)學講師，在 2016 年之后，他開始全身心投入 3b1b 的工作中。

如果你對自己的學習能力信心不足，或許看看 3b1b 的內(nèi)容會是一個好主意，全程動畫演示，讓你對知識點明白的徹徹底底。