正則化是一種強大的技術,通過防止過擬合來提高模型性能。本文將探索各種XGBoost中的正則化方法及其優勢。

為什么正則化在XGBoost中很重要?

XGBoost是一種以其在各種機器學習任務中的效率和性能而聞名的強大算法。像任何其他復雜模型一樣,它可能會過擬合,特別是在處理噪聲數據或過多特征時。XGBoost中的正則化有助于通過以下方式緩解這一問題:

1. 降低模型復雜度: 通過懲罰較大的系數,正則化簡化了模型。
2. 改善泛化能力: 確保模型在新數據上表現良好。
3. 防止過擬合: 防止模型過度適應訓練數據。

下面我們介紹在XGBoost中實現正則化的方法

1. 減少估計器的數量

減少估計器的數量可以防止模型變得過于復雜。兩個關鍵超超參數包括:

n_estimators: 設置較低的樹的數量可以幫助防止模型學習訓練數據中的噪聲。n_estimators的高值會導致過擬合,而低值可能導致欠擬合。

early_stopping_rounds: 這種技術在驗證集上的性能停止改善時停止訓練過程,防止過擬合。

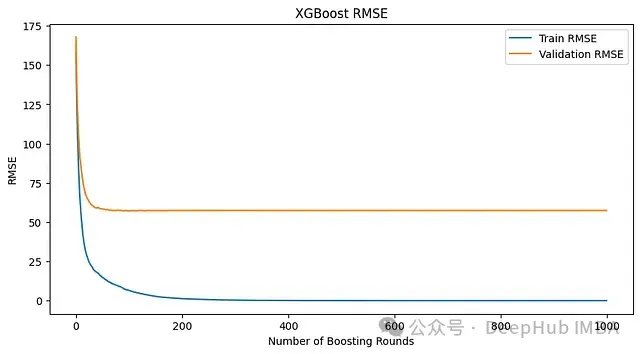
上圖為沒有早停的模型指標

上面的模型中,即使損失不再下降,訓練也會繼續。相比之下,使用early_stopping_rounds=10，當連續10輪損失沒有改善時,訓練就會停止。

# 初始化帶有早停的XGBoost回歸器
 model = xgb.XGBRegressor(n_estimators=1000, learning_rate=0.1, max_depth=5)
 
 # 使用早停訓練模型
 model.fit(X_train, y_train,
           eval_set=[(X_test, y_test)],
           early_stopping_rounds=10,
           verbose=True)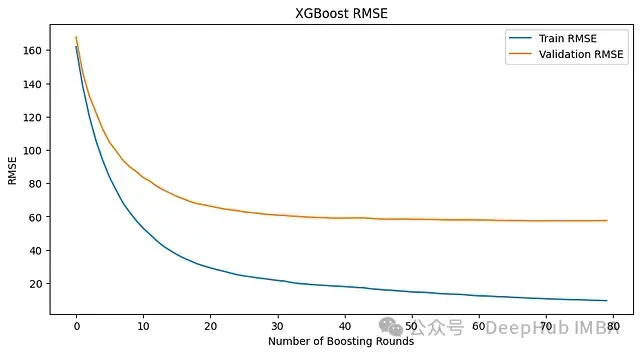

使用early_stopping_rounds=10的模型指標

2. 使用更簡單的樹

簡化每棵樹的結構也可以幫助正則化模型。關鍵參數包括:

gamma: 在葉節點上進行進一步分區所需的最小損失減少。較高的值會導致更保守的模型。

下面是XGBoost的目標函數。如果增加gamma,葉節點的數量(T)就會減少。gamma懲罰T并幫助防止樹變得過于復雜。

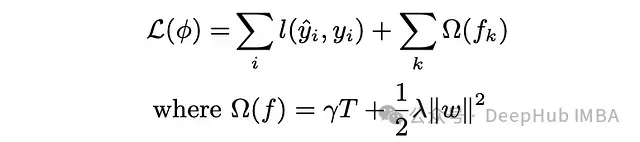
Gamma是一個后剪枝參數。以下復雜公式表示在每次分裂時計算的增益。第一、第二和第三項分別是左子節點、右子節點和父節點的相似度分數。Gamma(最后一項)是增益的閾值。

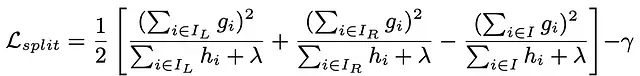
在下面的例子中,每個節點內的值代表不包含gamma項的增益。當gamma設置為400時,最底部的分支被刪除,因為它不滿足閾值標準,這樣樹就變得更簡單了。

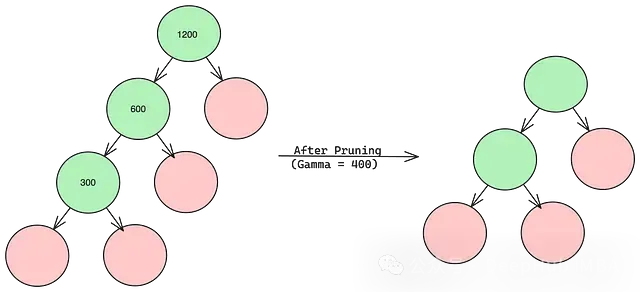
那么問題來了:gamma的最佳值是多少?答案在于超參數調優。

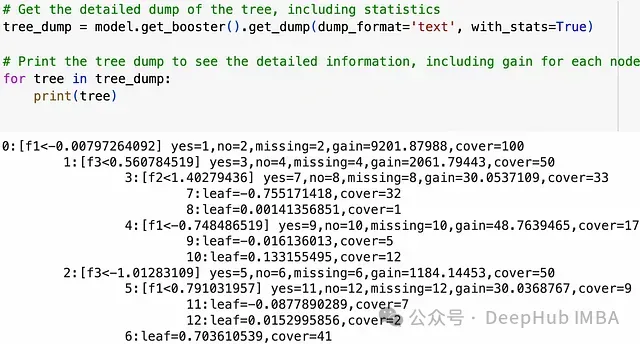
# 獲取樹的詳細轉儲,包括統計信息
 tree_dump = model.get_booster().get_dump(dump_format='text', with_stats=True)
 
 # 打印樹的轉儲以查看詳細信息,包括每個節點的增益
 for tree in tree_dump:
     print(tree)

上面的代碼將顯示所有決策樹的轉儲。通過觀察所有節點的增益,我們可以嘗試不同的gamma值。

import xgboost as xgb
 # Gamma的實現
 model = xgb.XGBRegressor(n_estimators=3, random_state=42, gamma = 25000)

但是有一點，gamma值過高會導致欠擬合,因為它減少了樹的深度,而gamma值過低會導致過擬合。

max_depth: 限制樹的最大深度。較低的值可以防止模型學習過于具體的模式。這是一個預剪枝參數。

思考題1:當我們有gamma時,為什么還需要max_depth?（答案在最后）

min_child_weight: 要解釋這個參數就要先了解什么是cover。

當我們進行樹轉儲時,我們會看到所有節點的cover值。Cover是hessians的總和,而hessian是損失函數相對于預測值的二階導數。

我們以一個簡單的損失為例，對于均方損失函數的回歸問題,hessian的值為1。所以在這種情況下,cover基本上是每個節點中的數據點數量。因此min_child_weight是每個節點中應該存在的最小數據點數量。它對每個節點設置以下條件:cover > min_child_weight。

xgboost中回歸問題的min_child_weight類似于決策樹中的min_sample_split。

import xgboost as xgb
 
 # min_child_weight的例子
 model = xgb.XGBRegressor(n_estimators=100, learning_rate=0.1, max_depth=5, min_child_weight=10, gamma=1, random_state=42)

對于分類問題,理解這一點有點棘手,但是簡單來說分類中min_child_weight的一句話描述是:它為數據點的重要性設置了一個閾值。

所以我們只要記住min_child_weight是一個預剪枝參數。增加min_child_weight會減少過擬合。

3. 采樣

采樣涉及在數據的子集上訓練模型,這可以通過引入隨機性來減少過擬合。

subsample: 用于訓練每棵樹的訓練數據的百分比。較低的值可以防止過擬合。子采樣使每個決策樹成為數據子集的專家,遵循"群眾的智慧"原則。根據數據的不同,0.5到0.8的范圍通常會給出良好的結果。

colsample: 用于訓練每棵樹的特征的百分比。這也可以用來引入隨機性并防止過擬合。colsample有以下三種類型,它們的值范圍從0到1。這些按引入隨機性的增加順序排列如下。假設我們的數據中有10個特征,所有這些超參數的值都設置為0.5:

• colsample_bytree : 為每棵樹隨機選擇5個特征,并根據這些特征進行分裂。
• colsample_bylevel : 為每個級隨機選擇5個特征,并根據這些特征進行分裂。
• colsample_bynode : 為每個節點隨機選擇5個特征,并根據這些特征進行分裂。

import xgboost as xgb
 
 # subsample和colsample的例子
 model = xgb.XGBRegressor(n_estimators=100, subsample=0.8,
                        max_depth=5, colsample_bytree=0.5,
                        colsample_bylevel=0.5, colsample_bynode=0.5)

4. 收縮

收縮減少了每棵單獨樹的影響,使模型更加穩健:

learning_rate (收縮): 減少每棵樹的影響。較低的值意味著模型構建更多的樹,但不太可能過擬合。0.3是許多模型的合適學習率。

lambda和alpha: L2(嶺)和L1(Lasso)正則化項,懲罰大系數。

當增益小于gamma時,該節點就會被剪枝。當lambda增加時,過擬合減少,欠擬合增加。Lambda與gamma一起用于正則化。

思考題2:當我們有gamma時,為什么還需要lambda?

import xgboost as xgb
 # reg_lambda是lambda的超參數,reg_alpha是alpha的超參數
 model = xgb.XGBRegressor(n_estimators=3, learning_rate=0.3, reg_lambda=100, reg_alpha=100, gamma=10000)

思考題答案

1、XGBoost中即使有了gamma參數，我們仍然需要max_depth參數。

在XGBoost中，gamma和max_depth雖然都用于控制樹的生長，但它們的工作方式和目的略有不同：

1. gamma（最小分裂損失）：

• gamma是一個后剪枝參數。
• 它控制節點分裂時所需的最小損失減少量。
• 如果分裂導致的損失減少小于gamma，那么這個分裂就不會發生。
• gamma更關注的是分裂的質量。

2. max_depth（最大樹深）：

• max_depth是一個預剪枝參數。
• 它直接限制了樹可以生長的最大深度。
• 無論分裂的質量如何，一旦達到max_depth，樹就會停止生長。
• max_depth更關注的是樹的整體結構。

為什么兩者都需要：

1.不同的控制粒度：

• gamma提供了一種基于性能的細粒度控制。
• max_depth提供了一種簡單直接的粗粒度控制。

2.計算效率：

• 只使用gamma可能導致在某些情況下樹過度生長，增加計算復雜度。
• max_depth可以有效地限制計算資源的使用。

3.模型可解釋性：

• 過深的樹可能難以解釋，即使每次分裂都是有意義的。
• max_depth可以保持樹的結構相對簡單。

4.處理不同類型的數據：

• 對于某些數據集，基于gamma的剪枝可能不夠，樹仍然可能過度生長。
• max_depth提供了一個絕對的上限。

5.互補作用：

• 兩個參數一起使用可以更靈活地控制模型的復雜度。
• 它們共同作用，可以在模型性能和復雜度之間取得更好的平衡。

總之，gamma和max_depth在控制樹的生長方面起著互補的作用。gamma關注分裂的質量，而max_depth確保樹不會變得過于復雜。同時使用這兩個參數，可以更好地平衡模型的性能、復雜度和可解釋性。

2、為什么在XGBoost中即使有了gamma參數，我們仍然需要lambda參數。

在XGBoost中，gamma和lambda雖然都用于正則化，但它們的工作方式和目的是不同的：

1. gamma（最小分裂損失）：

• gamma主要用于控制樹的生長。
• 它設置了節點分裂所需的最小損失減少量。
• 如果分裂導致的損失減少小于gamma，那么這個分裂就不會發生。
• gamma更關注的是樹的結構和復雜度。

2. lambda（L2正則化項）：

• lambda是應用于葉子權重的L2正則化項。
• 它直接懲罰模型的權重。
• lambda幫助防止模型對個別特征過度依賴。
• 它可以使模型更加穩定和泛化能力更強。

為什么兩者都需要：

1. 不同的正則化目標：

• gamma主要影響樹的結構。
• lambda主要影響葉子節點的權重。

2. 模型復雜度的不同方面：

• gamma通過限制樹的生長來減少復雜度。
• lambda通過縮小權重來減少復雜度。

3. 處理不同類型的過擬合：

• gamma可以防止模型學習訓練數據中的噪聲。
• lambda可以防止模型對某些特征過度敏感。

4. 互補作用：

• 同時使用這兩個參數可以更全面地控制模型的復雜度。
• 它們一起工作可以在模型的結構和權重上都實現正則化。

5. 靈活性：

• 在某些情況下，你可能想要一個深度較大但權重較小的樹，或者相反。
• 有了這兩個參數，你可以更靈活地調整模型以適應不同的數據集和問題。

6. 收縮效果：

• 如之前提到的，lambda還有一個額外的作用，就是對樹的輸出進行收縮。
• 這種收縮效果可以進一步幫助防止過擬合，特別是在梯度提升的早期階段。

gamma和lambda在XGBoost中起著互補的作用。gamma主要控制樹的結構，而lambda主要控制葉子節點的權重和樹的輸出。同時使用這兩個參數，可以更全面、更靈活地控制模型的復雜度，從而在不同層面上防止過擬合，提高模型的泛化能力。這種多層面的正則化策略是XGBoost強大性能的關鍵因素之一。