6700萬參數比肩萬億巨獸GPT-4!微軟MIT等聯手破解Transformer推理密碼
「因果推理」絕對是當前GenAI熱潮下的小眾領域,但是它有一個大佬級的堅定支持者——Yann LeCun。
他在推特上的日常操作之一,就是炮轟Sora等生成模型,并為自己堅信的因果推理領域搖旗吶喊。
甚至,早在2019年VentureBeat的采訪中,他就表達過這一觀點:我們需要在深度學習模型中引入事件的因果關系,才能增強泛化能力,減少訓練數據使用。

對于當前最流行的模型架構Transformer,我們能教它因果推理嗎?
最近,來自微軟MIT等機構的研究人員提出了一種訓練大模型新范式——公理框架(Axiomatic Framework)。
論文中,作者從頭開始訓練了6700萬參數的模型,僅使用了簡單的因果鏈作為訓練數據。
令人驚訝的是,在推斷復雜圖表中的因果關系時,67M模型的表現超越了十億級參數LLM,甚至可以與GPT-4相媲美。

論文地址:https://arxiv.org/abs/2407.07612v1
微軟MIT等團隊最新方法的提出,是受到了圖靈獎得主Judea Pearl啟發。

Pearl曾提出了結構化因果規則中的因果無關性公理,即直接通過符號化公理示例來教Transformer模型學習被動數據(passive data)。
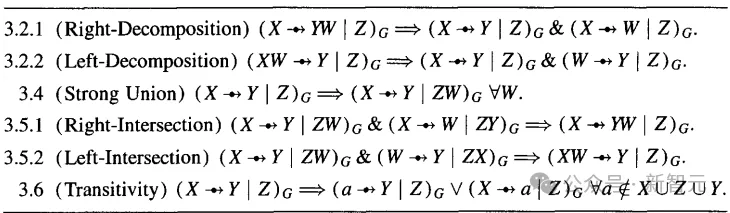
這種方法不同于傳統機器學習模型,使用由公理推導出的數據。
正如結果所示,通過公理訓練,研究證明了Transformer模型可以學習因果,從而推斷因果關系,并從相關性中識別因果性。
這暗示了,像GPT-4等大模型的訓練,可以通過網絡數據中的帶噪聲的公理化示例學習因果知識,而無需進行干預實驗。

網友稱贊道,「研究者的觀點非常耐人尋味,因果推理一直是LLM的致命弱點,進一步發展這一領域,勢在必行」。

「這類研究可能是通向半AGI的一條途徑」。

研究背景
因果推理(causal reasoning)是一種推理過程,遵守有特定因果性的預定義公理或規則。
圖靈獎得主Judea Pearl曾通過如下的「因果關系階梯」(ladder of causation)定義了可能的因果推理類型。
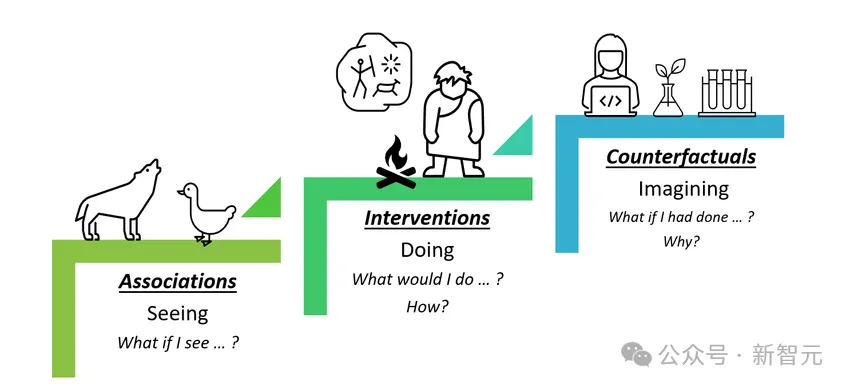
通常因果推理所用的公理或規則并不會被直接引入,模型學習的只是數據。公理或規則作為歸納偏差被納入模型,比如通過正則化、模型架構或變量選擇等方式。
而這篇論文想要探討的,就是模型能否從被動的符號演示中直接學習公理或規則。作者將這種方法稱為「公理化訓練」(axiomatic training)。
假設因果公理都可以以如下形式表示:<前提,假設,結果>,其中結果只有「是」和「否」兩種形式。
這基本類似于亞里士多德提出的「三段論」格式,比如Judeal Pearl書中提出的「碰撞公理」(collider axiom)就可以表示為:
前提:?????, ???????, ???????
假設:A是否導致C?
結論:是
這只是單個公理的表示,那么如何表達一個復雜系統中多個公理的組合呢?甚至,我們能用有限數量的公理表達任意因果模型嗎?
此處,論文引用了Judea Pearl和David Galles在1997年發表的一項研究,他們證明了,對于給定的穩定概率因果模型,都存在一組有限公理,可以充分表征對應的有向因果圖。
因果模型M=(X,U,F)被定義為內部變量X、外部變量U和一組結構方程F的集合,結構方程描述了變量X和U之間的因果關系。
模型M的另一種等效表示方式就是有向圖G,用有向邊Vi?Vj表示兩個節點Vi和Vj之間的因果關系。
所謂的「穩定概率」(stable probabilistic)因果模型,是指他們對模型作出的穩定性假設,指M中所有的不相關性(X ? Y|Z)都是穩定的,寫作:
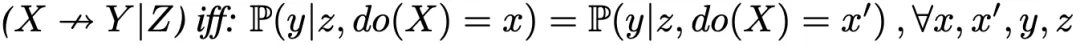
在穩定性假設下,Galles和Pearl共描述了6個公理,而這篇論文主要關注傳遞性公理。對于穩定概率的因果模型,給定系統中的變量X、Y、Z,傳遞性公理可以寫作:
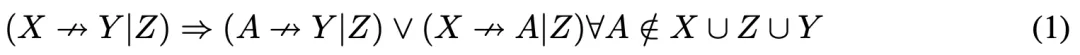
將上述表達式通過取反進一步簡化,可以寫出其含有因果相關性的版本:
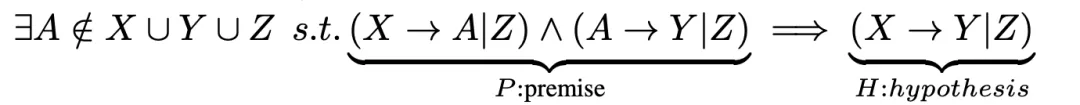
其中表達式左側即為前提,右側即為假設。
這樣的公理可以派生出數千個合成的符號表達式,從而用于向Transformer模型「教授」特定公理。
公理化訓練
訓練數據
上述含有前提和假設的公理能映射到「是」或「否」的標簽,一條訓練數據就可以表示為{(P,H,L)}的元組形式。
給定一個真實的因果圖,就可以通過應用傳遞性公理(一次或多次),枚舉出所有可能的N個元組{(P,H,L)},從而構建出數據集D。
比如,因果圖中包含X1?X2?X3?…?Xn這樣的鏈拓撲時,一個可能的前提是X1?X2∧X2?X3,相應的假設X1?X3的標簽為「是」,而另一個假設X3?X1標簽就為「否」。
值得注意的是,論文中為了表達的清晰性,使用了數學語言進行描述,但實際上用于訓練的數據集只包含自然語言。
比如,上面例子中的前提應該表達為「X1導致X2,且X2導致X3」。
數據擾動:泛化的關鍵
之前有研究表明,以「擾動」(perturbation)形式增加訓練數據的可變性與多樣性,有助于提升模型的泛化能力。
因此,作者在不同層次上對訓練數據引入結構化擾動,以最大化數據集分布的多樣性。
1)節點名稱:傳遞鏈上每個節點的名稱都由1~3個字母/數字組成,長度和使用的特定字符是隨機生成的。
2)因果圖拓撲結構:主要包含兩種類型
- 順序結構(sequential):所有的因果邊方向都是從后向前,共同形成一個典型的「傳遞鏈」,比如X?Y?Z這種形式
- 隨機翻轉(random flipping):給定一個順序結構的傳遞鏈,對其中一些邊進行隨機翻轉,從而引入復雜性。比如X?Y?Z可以被修改為X?Y?Z。
隨機翻轉可以在單一方向的鏈中添加分叉結構(X?Y?Z,fork)和碰撞結構(X?Y?Z,collider),它們是任何有向因果圖的基本構建塊,有助于提升模型進行跨結構泛化的能力。
3)鏈長度:訓練集中加入了長度不等的鏈,包含3~6節點。
損失函數
論文沒有采用訓練Transformer模型常用的next token預測損失,而是根據給定數據集中每個元組的真實標簽進行定義,表示為:
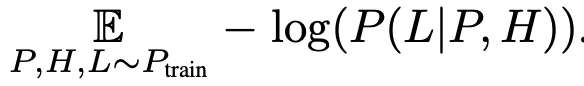
位置編碼
除了訓練數據和損失函數之外,另一個重要因素是位置編碼的選擇。
之前有研究表明,位置編碼機制對Transformer的序列長度泛化能力有明顯影響,但不同的研究似乎得出了互相矛盾的結果。
因此,作者在研究中分別嘗試了不同的方法,包括可學習位置編碼(LPE)、正弦位置編碼(SPE)和無位置編碼(NoPE)。
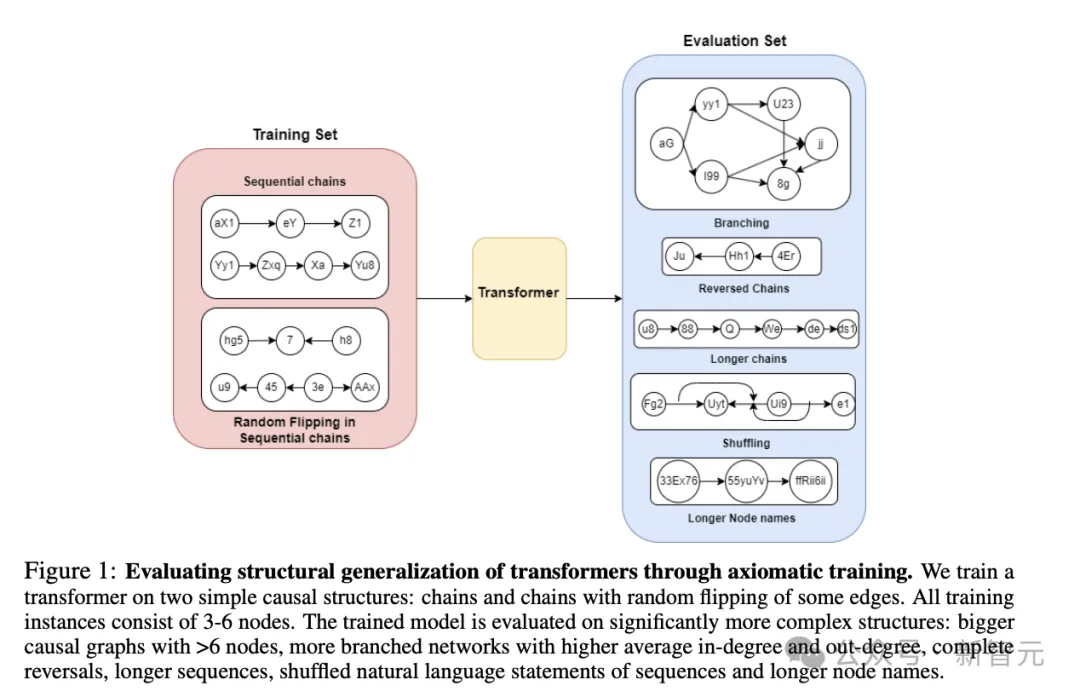
訓練和評估的整體流程如圖1所示,Transformer模型在順序鏈和帶有隨機翻轉的鏈上訓練,長度為3~6個節點。
之后,訓練過的模型在具有>6個節點的更復雜結構上進行評估,其中節點平均的出度(out-degree)和入度(in-degree)都更大,序列更長,且引入了分支、反轉(reversal)等復雜變化。
實現細節:架構、分詞器和訓練過程
具體來說,研究人員基于GPT-2的架構,訓練了一個擁有6700萬參數的解碼器模型。
該模型有12個注意力層、8個注意力頭,以及512個嵌入維度。
值得一提的是,67M模型是在各種訓練數據集上,從頭開始訓練的。為了理解位置編碼(PE)的影響,他們考慮了正弦位置編碼(SPE)、可學習位置編碼(LPE)以及不使用位置編碼(NoPE)三種情況。
所有模型都使用AdamW優化器進行訓練,學習率為1e-4,訓練100個epoch。
由于訓練數據集遵循特定結構,研究人員還開發了一個自定義分詞器(custom tokenizer)。
字母數字節點名稱在字符級別進行分詞,而像「causes」、「cause」、「Does」、「Yes」「No」這樣的特殊術語則在詞級別進行分詞。
簡言之,字符級分詞用于字母數字節點名稱,詞級分詞用于特殊術語。
這種方法可以避免在測試時,出現詞匯表外(OOV)token,因為測試集中的字母數字節點名稱可能與訓練集中的不同。
采用這種方法后,6700萬參數Transformer模型的詞匯表大小為69。
實驗結果
復雜因果場景的泛化
研究人員首先展示了,通過公理化訓練的Transformer模型在泛化到更大、更復雜的因果圖方面的表現,并將其與預訓練的大模型進行了比較。
序列長度泛化
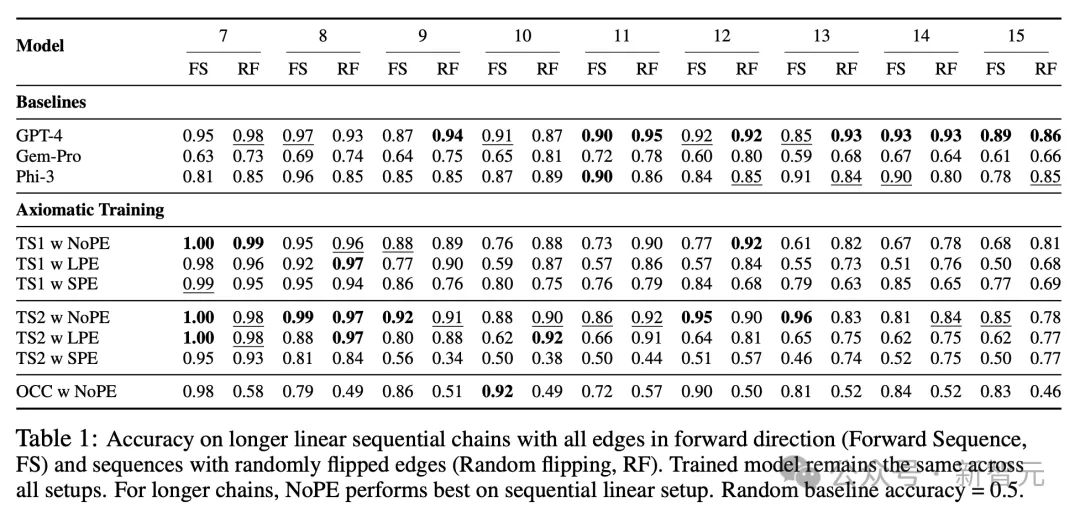
表1展示了不同模型在評估訓練過程中,未見過的更長因果鏈時的準確率。
在基線預訓練語言模型中,GPT-4在標準和隨機翻轉的因果鏈上都取得了最高的準確率。
令人驚訝的是,盡管TS2(NoPE)模型在訓練過程中從未見過更長的序列,但它的表現能夠與萬億參數規模的GPT-4模型相媲美。
雖然訓練時只用到了長度為3~6個節點的因果鏈,但序列長度為7~13時,TS2(NoPE)在標準和隨機翻轉的鏈上,獲得了比GPT-4更高或相當的準確率。
對于序列長度為14-15的情況下,其準確率有所下降(標準鏈為0.85,隨機翻轉鏈為0.78),但仍然顯著高于Gemini-Pro 、Phi-3模型。
需要注意的是,隨機預測會得到50%的準確率,這表明通過公理化訓練的TS2(NoPE)模型,能夠將其推理能力泛化到更長的序列上。
節點名稱轉變
對于在TS2數據集上訓練的模型,研究人員還評估了其對變量名稱變化的泛化能力(圖 3)。
結果發現,TS2(NoPE)對節點名稱的變化很穩健,在引入新的、更長的名稱時仍能保持較高的準確率。它還保持了對新節點名稱較長序列的通用性,其表現與GPT-4相似。

因果序列順序
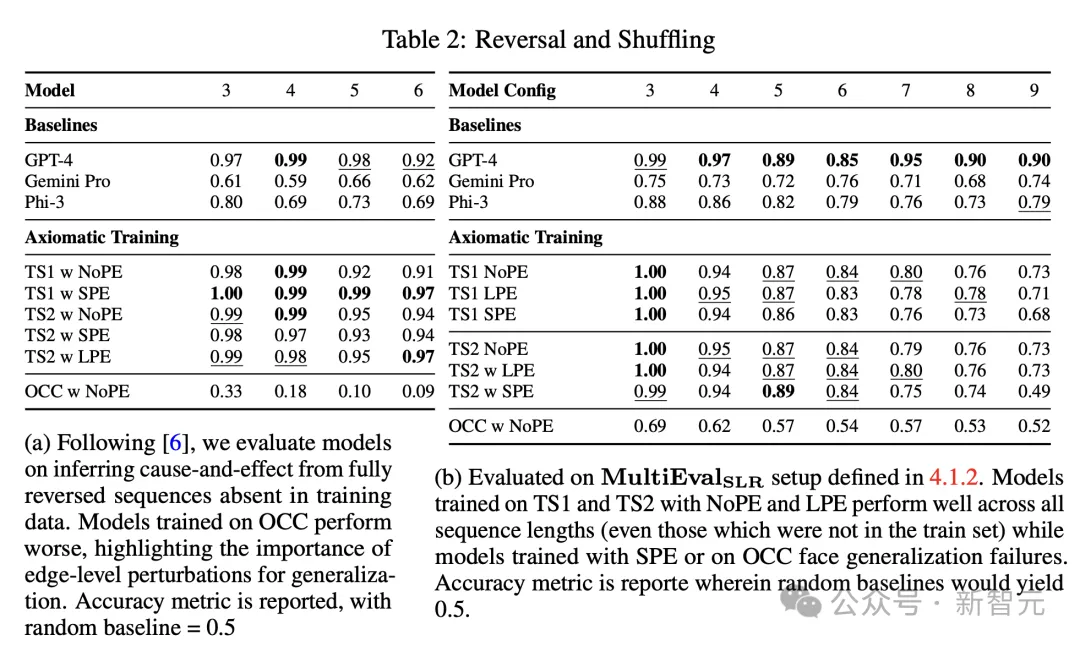
與長度和節點名稱的變化不同,反轉(reversal)以及分支(branching)操作改變了因果結構,因此能更好地評估模型是否學習到了對結構的準確表示。
在表2b中,TS2(NoPE)在長度不超過8的因果鏈上,獲得的準確率高于Gemini Pro、Phi-3。長度為9時,TS2(NoPE)的準確率為0.73,與Gemini Pro(0.74)相當。
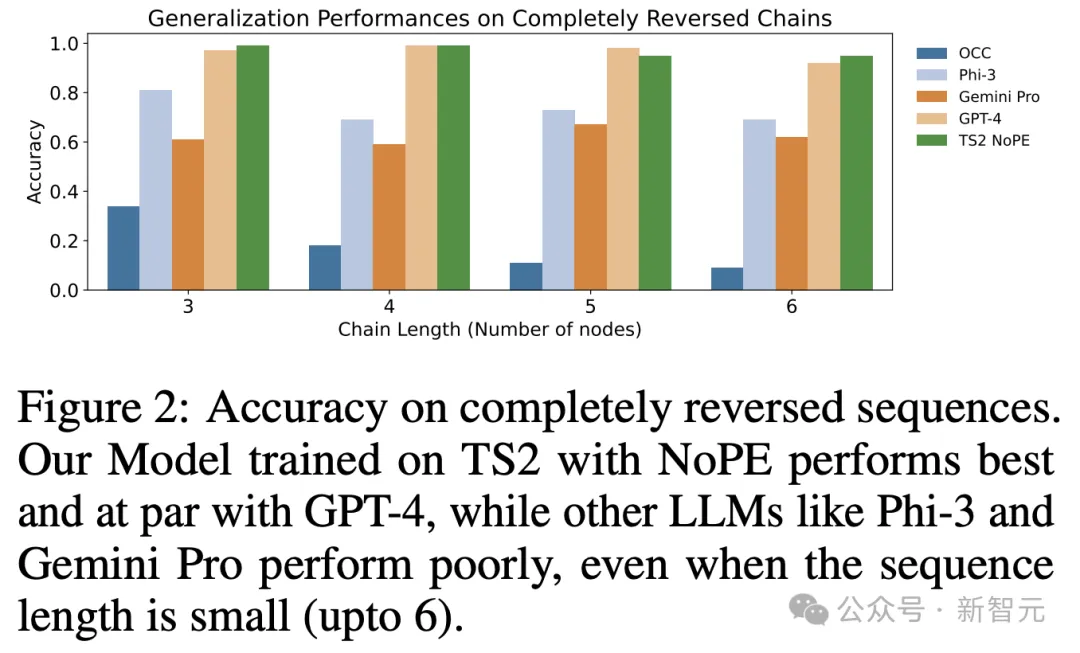
在表2a中,研究者還觀察到對完全反轉序列進行評估的類似模式。
在這項任務中,公理訓練模型TS2(NoPE)在限制鏈長度為3-6時,表現優于GPT-4。特別是,其準確率(長度為 6 的鏈為0.94)大大高于Gemini Pro和Phi-3(分別為0.62和0.69)。
分支(Branching)
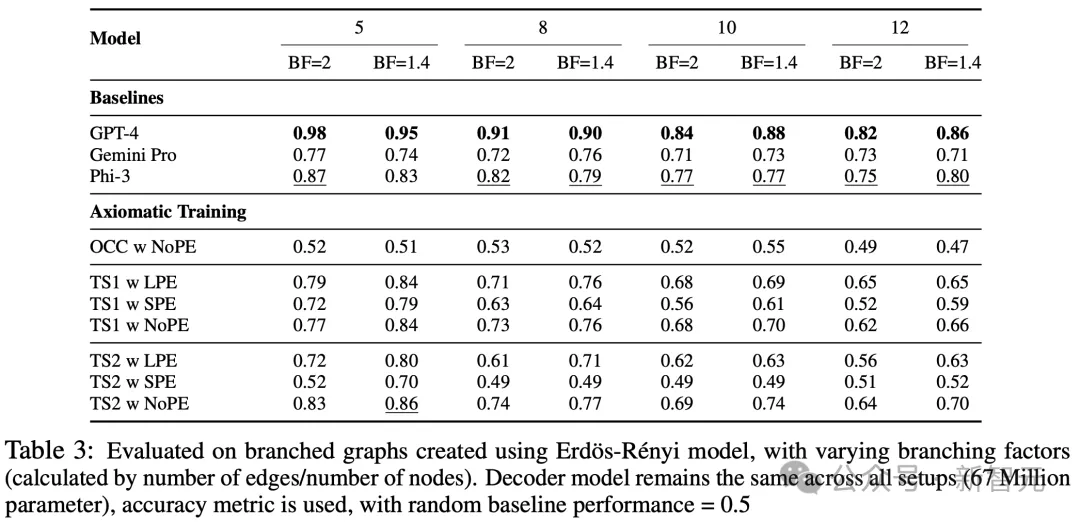
分支可能是最有挑戰性的任務,因為它引入了在訓練期間未見的新結構。
雖然GPT-4在圖大小不斷增大的情況下獲得了最佳準確率,但TS2(NoPE)模型在除一個節點外的所有圖大小上,都比Gemini Pro獲得了更高的準確率。
即使在有12個節點和1.4個分支因子的圖形上進行評估,TS2(NoPE)模型也能獲得70%的準確率,明顯優于隨機模型(50%)。
總結
在所有評估設置中,公理化訓練模型TS2(NoPE)的性能明顯優于隨機基線,即使因果鏈的長度超過其訓練數據。
特別是,模型沒有在完全反轉的鏈上進行訓練,它的表現也與規模更大的GPT-4模型相當(圖 2)。
在其他任務中,它的準確性往往優于或與Gemini Pro、Phi-3等十億參數規模的模型相當。
這些結果表明,經過公理訓練的模型可以從簡單因果序列的演示中,學會推理更復雜的因果結構。這表明公理訓練在因果圖推理方面的潛力。
其他結果:數據多樣性和位置編碼的作用
位置編碼的作用
比較不同位置編碼選擇的模型性能,研究人員發現沒有位置編碼的模型在更長的序列(最長到15個節點的鏈)和復雜的、未見過的圖結構上都能很好地泛化,盡管它們僅在3-6個節點的鏈上進行訓練。
使用正弦位置編碼(SPE)和可學習位置編碼(LPE)的模型在更長的鏈上表現也不錯,但當節點名稱長度增加時表現較差,即使是在節點數較少的鏈上也是如此(圖3)。
這種使用SPE和LPE的泛化失敗,突出了模型無法處理訓練集中序列的微小擾動。
此外,SPE在不同的結構維度上表現不佳(如分支)以及基于順序的設置(shuffling和反轉)。
可學習的位置編碼在長度達9的線性鏈上表現良好,但之后急劇下降。
總的來說,研究結果擴展了早期關于不使用位置編碼(NoPE)有效性的研究,將其應用于理解因果序列的任務,并在測試時泛化到更長的長度和復雜的結構。
數據擾動的重要性
除了位置編碼外,訓練數據中序列的多樣性也起著重要作用。
僅在因果鏈上,訓練的模型可以泛化到較長的鏈(表 1),但不能泛化到其他DAG結構(見圖4中的翻轉,圖2中的反轉,表3中的分支)。
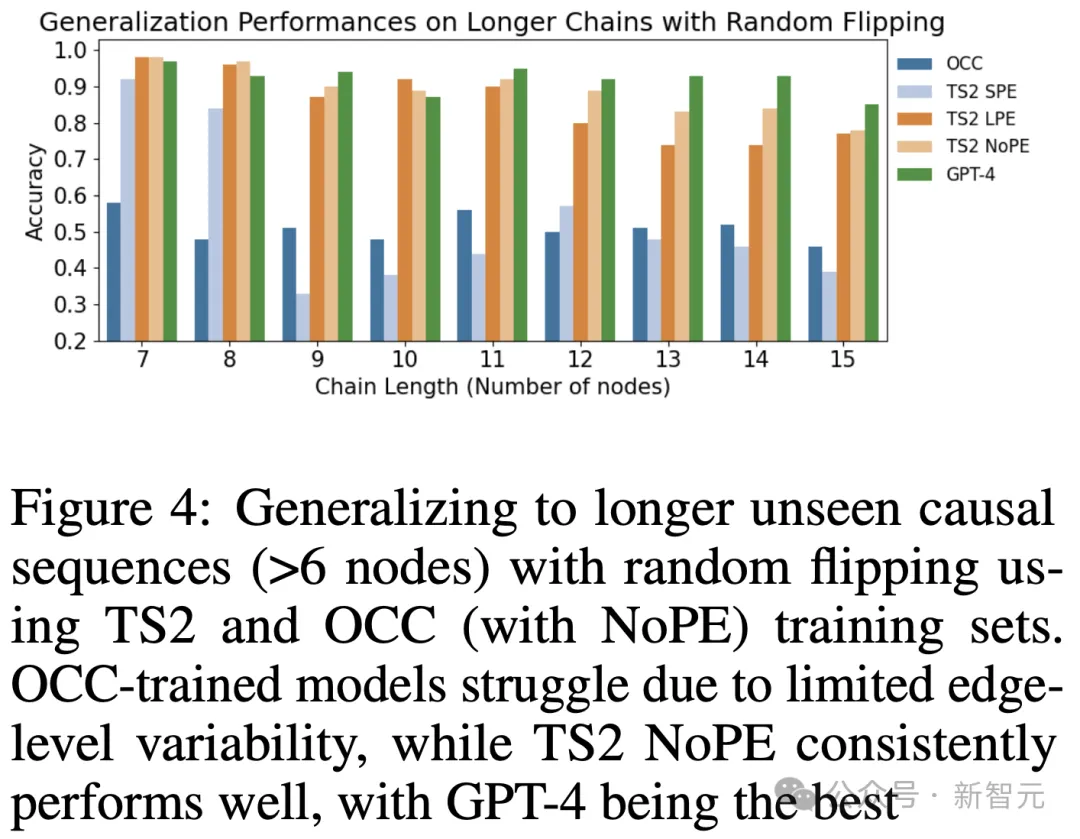
在TS1或TS1上訓練的模型在所有情況下都具有通用性,包括隨機翻轉、順序排列和分支;因此突出了通過隨機翻轉在邊水平上納入可變性的影響。
不過,在不同任務中,研究發現TS2的準確率高于TS1,即使TS1因隨機翻轉而產生了更多變化。
這表明,雖然擾動有助于結構泛化,但過度的擾動可能會阻礙結構泛化。
使用公理訓練從相關性推斷因果關系
接下來,作者研究這種能力是否可以轉移到其他因果任務上。
為此,研究人員將公理化訓練應用于一個任務,該任務是從觀察數據中的相關性陳述推斷因果關系。
如圖5所示,每個數據實例包括用自然語言描述的3到6個節點圖的相關關系;目標是推斷假設的真值,判斷任何給定節點之間是否存在直接或間接關系,以及可能存在的碰撞節點和混雜因素。
這個任務比應用傳遞性公理要困難得多。

由于任務的復雜性,結果發現像Gemini Pro、Phi-3這樣的預訓練模型的表現與隨機猜測相似(準確率為52%)。
雖然GPT-4的表現稍好一些,但其性能仍然較低(準確率為58%)。
值得注意的是,研究者的小型Transformer模型表現優于所有基線模型,準確率達到64%,比GPT-4高出6%。
通過進一步探索不同的訓練設置,公理化訓練的Transformer模型可能會在這類因果推理任務上得到進一步的優化。
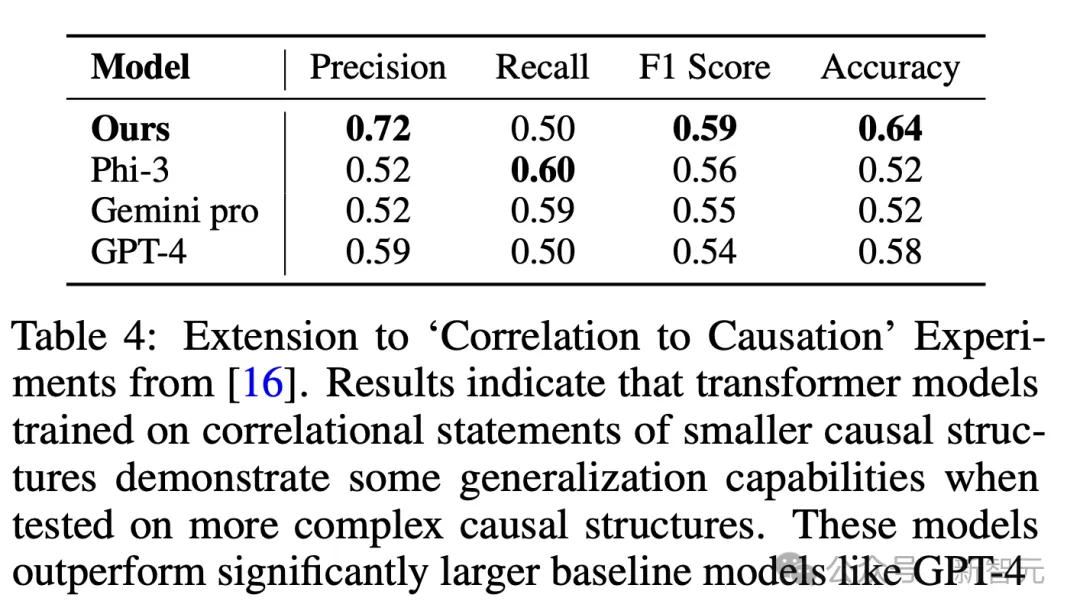
總的來說,研究人員認為公理化訓練是教Transformer模型學習因果關系的一種很有前景的方法。
受Judea Pearl愿景的啟發,這項工作代表著一個潛在的新科學前沿——因果關系研究和語言模型的交叉點上。












































