用于時間序列中的變點檢測算法,你學會了嗎?
假設你正在進行運動時,使用數字設備監測心率。你先跑了四分之一公里,然后走了十分鐘,接著又跑了四分之一公里里。可能你的心率情況與圖 (1) 中的時間序列相似。圖中展示了一段高心率、一段低心率,然后又回到高心率。時間序列的突然變化提示我們,你的活動狀態發生了重大變化。
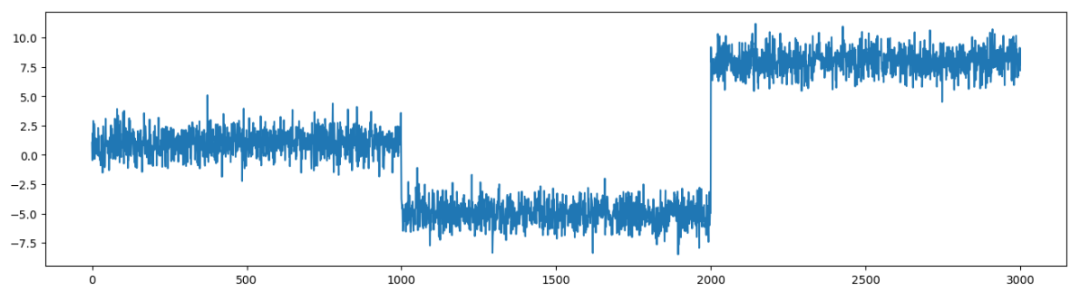 圖 (1)
圖 (1)
變點檢測是指在時間序列中發生了重大結構性斷裂或者轉變的點,這些變化可能是由于數據生成、技術或消費者行為等外部因素造成的。檢測這些變點非常重要,因為它有助于我們理解和量化變化。我們需要及時準確地檢測這些變化并立即發出警報。
Change point detection (CPD) 被稱為變點檢測,其基本定義是在一個序列或過程中,當某個統計特性(分布類型、分布參數)在某時間點受系統性因素而非偶然因素影響發生變化,我們就稱該時間點為變點。變點識別即利用統計量或統計方法或機器學習方法將該變點位置估計出來。
CPD在金融、醫療保健和環境監測等諸多領域都有著廣泛的應用。其中,它在質量控制過程中可以幫助識別產品或服務質量的變化,也可以應用于醫療診斷,幫助確定病人的健康狀況或疾病的變化。舉個例子,重癥監護室(ICU)中的病人需要持續進行心率監測,而及時發現心率的任何變化并迅速提醒醫生做出反應對于病人的生命至關重要。
在CPD中,我們主要尋找時間序列中基本統計屬性(比如均值、方差或自相關性)發生明顯變化的點。雖然有多種算法可以檢測這些變化點,但一個重要的方面是要明確數據類型(即實時數據流還是離線數據),因為這將決定算法的選擇和發展。
算法取決于實時數據還是離線數據
CPD算法的運行方式取決于數據的類型,即實時數據或離線數據。對于離線數據,我們可以利用歷史數據來分析整個序列,這種情況下適用的是離線CPD。離線CPD涉及分析已經收集的數據集,適用于歷史數據分析或檢測數據集中的異常情況。
然而,在實時環境中,我們需要快速檢測變點,而此時并沒有歷史數據可用。舉例來說,無人機每秒都會向家庭設備發送位置信息流,我們無法等待并長時間收集數據來檢測變化。在線視頻流也是一個例子。實時CPD需要在數據流到達時對其進行監控,并立即做出響應。這種情況常出現在許多實時應用中,比如金融市場監控、欺詐檢測或關鍵基礎設施監控。
對于離線 CPD,我們將引入Ruptures Python 模塊。對于實時 CPD,我們將演示changefinder模塊。
生成數據
生成兩個時間序列來測試算法。
- 恒定方差 (ts1):有十個數據段,方差恒定。
- 變化方差 (ts2):有十個數據段,但方差變化。
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
# Example 1: 恒定方差
ts1 = []
mu, sigma, seg = 0.0, 1.0, 1000
for i in range(10):
ts = np.random.normal(mu, sigma, seg) + np.random.randint(low=-10, high=10)
ts1 = np.append(ts1,ts, axis=0)
plt.figure(figsize=(16,4))
plt.plot(ts1)
# Example 2: 變化方差
ts2 = []
mu, sigma, seg = 0.0, 1.0, 1000
for i in range(10):
sig = np.random.randint(low=1, high=50)
ts = np.random.normal(mu, sigma * sig, seg)
ts2 = np.append(ts2,ts, axis=0)
plt.figure(figsize=(16,4))
plt.plot(ts2)圖(2)顯示了時間序列。第一個時間序列中的變點比較容易發現,而第二個時間序列中的變點就比較難發現了。
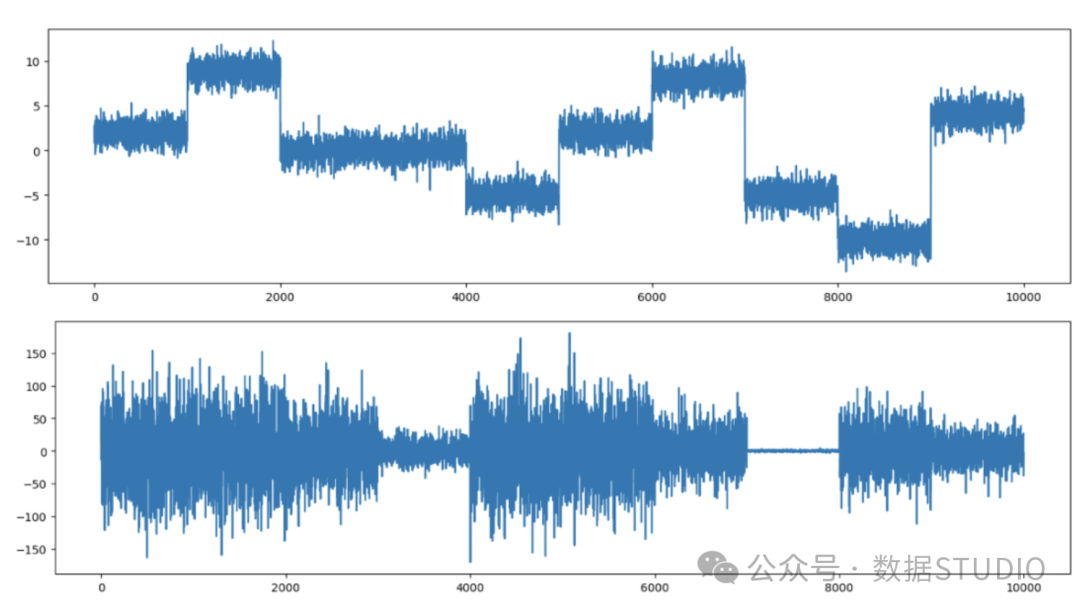 圖(2):恒定方差時間序列和變化方差時間序列
圖(2):恒定方差時間序列和變化方差時間序列
離線 - ruptures模塊
在離線分析中,我們能夠利用時間序列的歷史數據。對于 CPD,我們可以應用線性回歸的概念。然而,如果存在變點,直線就無法很好地擬合數據,這時候分段線能夠更好地適應數據。建立分段線的一種直觀算法是確定變點作為斷點。這種方法被稱為 精確線性時間(PELT)。
圖 (3.A) 和圖 (3.B) 解釋了PELT。在時間序列中(藍色顯示)存在一個變點和兩個分段。橙色線代表了回歸線,而橙色的垂直線表示了各點(用白色圓圈表示)到回歸線的距離。通過最小化所有數據點的距離之和來確定回歸線。
 圖 (3):剪枝后的精確線性時間(PELT)
圖 (3):剪枝后的精確線性時間(PELT)
在圖(3.B)中,分段線更適合數據。實際點到線條的距離和小于圖(3.A)中的距離之和。該算法通過從時間序列的左側滑動到右側來找到合適的變點,使得距離或誤差之和最小。
下面是用于搜索變點數量和位置的算法。C(.)代表距離或成本函數。我們還需要控制不要創建過多的線段,以防止對時間序列進行過度擬合。因此,b(β)項作為懲罰線段數量的參數,以防止搜索生成過多的線段。
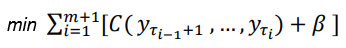 圖片
圖片
該算法在Python 模塊ruptures中編碼。
首次使用,需要用 pip install ruptures 安裝。
(1)恒定方差
# !pip install ruptures
import ruptures as rpt
# Detect the change points
algo1 = rpt.Pelt(model="rbf").fit(ts1)
change_location1 = algo1.predict(pen=10)
# Point the change points:
def plot_change_points(ts,ts_change_loc):
plt.figure(figsize=(16,4))
plt.plot(ts)
for x in ts_change_loc:
plt.axvline(x,lw=2, color='red')
plot_change_points(ts1,change_location1)圖 (4) 顯示,算法檢測到了所有十個變化點。
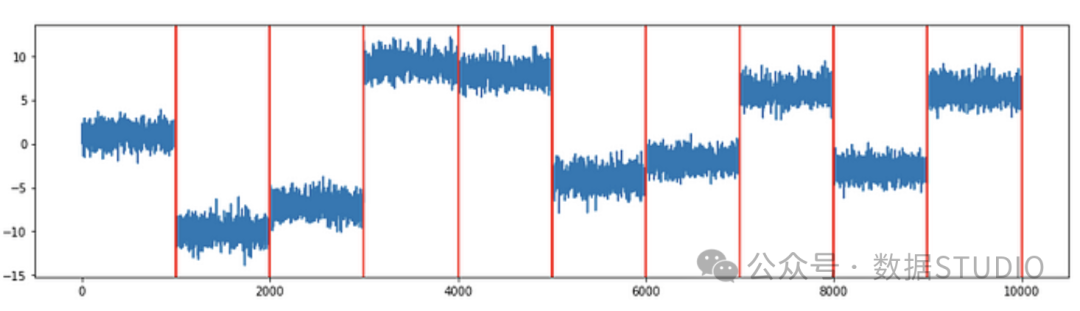 圖 (4):檢測到恒定方差時間序列的所有十個變點
圖 (4):檢測到恒定方差時間序列的所有十個變點
當方差隨時間變化時,CPD 是否仍然有效。
(2)變化方差
圖 (5) 顯示 PELT 算法在[3000, 4000, 6005, 7000, 8000, 8995, 10000]處發現了變點。
# detect the change points #
algo2 = rpt.Pelt(model="rbf").fit(ts2)
change_location2 = algo2.predict(pen=10)
change_location2
# Plot the change points #
plot_change_points(ts2,change_location2)我們知道應該有兩個變點 [1000, 2000, 5000]。但由于這些點前后的數據過于相似,PELT 無法發現這些差異。
 圖 (5):PELT 檢測到變化方差時間序列的一些變點
圖 (5):PELT 檢測到變化方差時間序列的一些變點
當使用 PELT 算法時,找到圖(4)以及圖(5)中的變化點可能需要相對較長的處理時間,特別是針對圖(5)。這樣可能無法滿足實時流數據的需求。因此,為了實時應用,我們設計了名為changefinder 的 Python 模塊。
實時 CPD
時間序列可以用自回歸(AR)移動平均過程來描述。在AR模型中,下一個數據點是過去數據點的加權移動平均值,并且帶有隨機噪聲。具體而言,下式表示了AR模型,其中 θi 是過去 p 個數據點的權重。
 圖片
圖片
如果存在一個變點,那么預計變點前后的自回歸過程將是不同的。 基于這種直覺,Yamanishi & Takeuchi 提出了順序貼現自回歸(SDAR)學習算法,這種直覺推動了他們的研究。SDAR 方法包括兩個學習階段。在第一個學習階段,它生成一個被稱為"異常分數"的中間分數。在第二個學習階段,它生成可以檢測變點的“變點分數”。以下是該算法的概述。
- 第 1 個 AR 模型 讀入一大塊數據 t = 1, ..., N, 然后建立一個 AR(自動回歸)模型。然后產生一個 "異常得分",即 AR 預測的 Xt 值與實際數據 Xt 之間的差值。請注意,在這一步驟中只提取了 N 個數據點。由于它不使用整個歷史數據,因此是為在線數據流設置的。
- 第 1 次平滑處理上述異常得分將非常不穩定,并產生錯誤信號。該算法為異常得分生成移動平均值 Yt,以平滑異常值。
- 第 2 個 AR 模型為 Yt 建立一個 AR 模型,并根據新建立的 AR 模型和 Yt 生成另一個 "異常得分"。
- 第 2 次平滑,同樣,新的異常得分也會出現波動。算法會生成移動平均值來平滑。如圖(6)所示,最終生成的分數稱為 "變點分數"。
這種算法不需要整個時間序列來檢測變點,因此大大減少了計算時間。
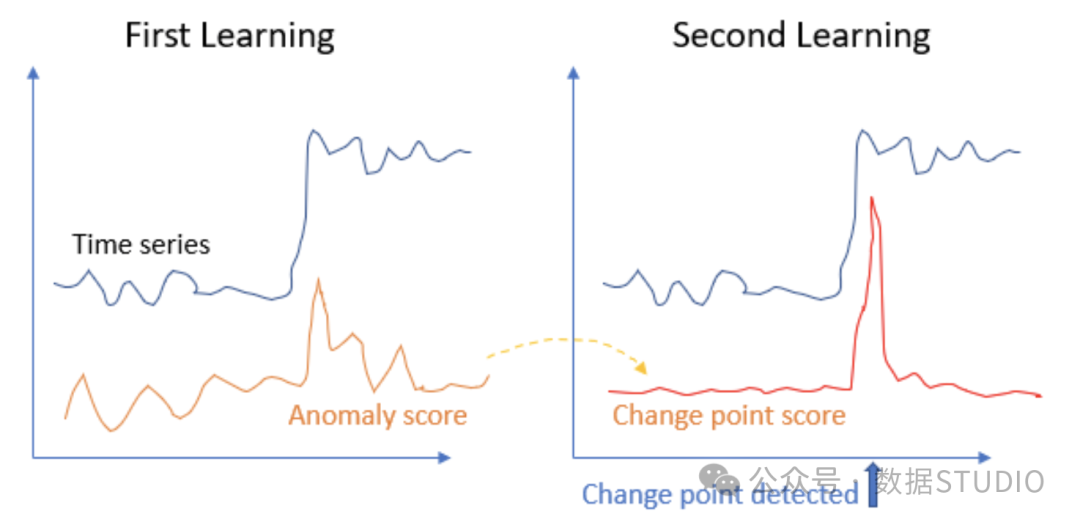 圖 (6):順序貼現自動回歸(SDAR)學習算法
圖 (6):順序貼現自動回歸(SDAR)學習算法
來研究兩種時間序列情況。
(1)恒定方差
適用于恒定方差時間序列 (ts1) 的前述代碼。Changefinder 需要三個參數:
- r:貼現率(0 至 1)。較高的貼現率會導致過去的時間序列迅速減少,意味著您可能不希望從過去的時間序列中學習。建議設置為 0.01。由于貼現率不是很敏感,設置為 0.01 或 0.05 都是可以的,可以自行嘗試。
- order:AR 模型階數
- smooth:用于計算平滑移動平均值的最近 N 個數據的大小。
在 changefinder 模塊中,我們對變點得分非常感興趣,它可以顯示時間序列是否突然偏離其常態。
# !pip install changefinder
import changefinder
def findChangePoints(ts, r, order, smooth):
'''
r: Discounting rate
order: AR model order
smooth: smoothing window size T
'''
cf = changefinder.ChangeFinder(r=r, order=order, smooth=smooth)
ts_score = [cf.update(p) for p in ts]
plt.figure(figsize=(16,4))
plt.plot(ts)
plt.figure(figsize=(16,4))
plt.plot(ts_score, color='red')
return(ts_score)
ts_score1 = findChangePoints(ts1, r = 0.01, order = 3, smooth = 5)圖 (7) 顯示了第一張圖中的 ts1,第二張圖中的紅色時間序列是變點分數。發生變化的位置就是那些大的變點分數。
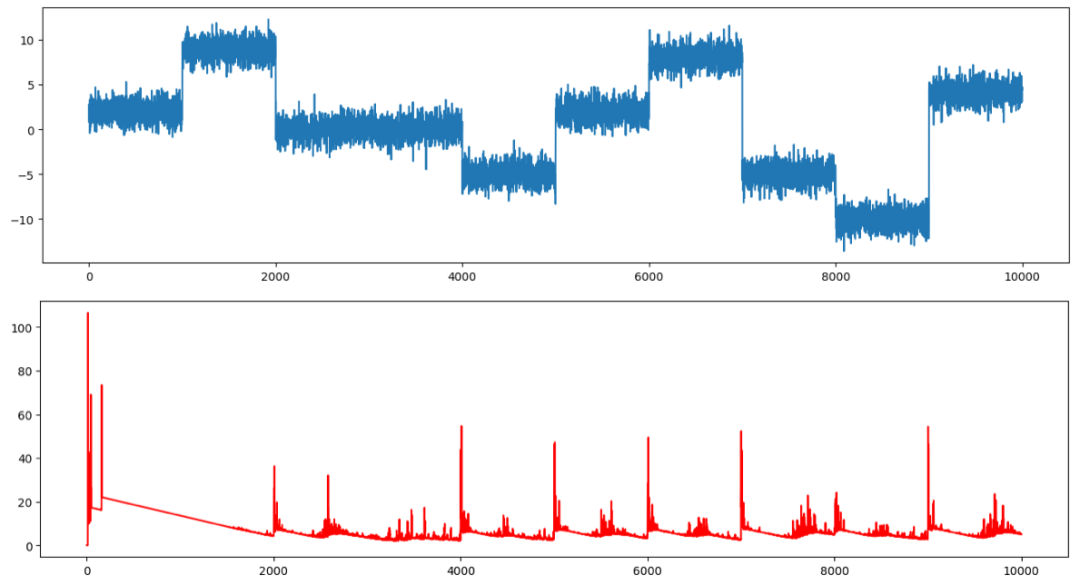 圖 (7):針對恒定方差時間序列的 SDAR 算法的變點得分
圖 (7):針對恒定方差時間序列的 SDAR 算法的變點得分
在此,我打印出了前 20 名的位置(您可以選擇更多)。
ts_change_loc1 = pd.Series(ts_score1).nlargest(20)
ts_change_loc1 = ts_change_loc1.index
np.sort(ts_change_loc1)array([ 11, 12, 13, 42, 43, 159, 160, 4001, 4008,
5001, 5007, 5008, 6007, 6008, 7000, 7001,
9000, 9001, 9007, 9008])總的來說,考慮到這是實時操作,該算法做得還不錯。它能檢測到許多變點,但卻漏掉了 1000、2000 和 8000 個點。這是因為這些點之前和之后的數據頻率過于相似,不符合差異條件。在運行代碼時,您可能會發現計算時間比破裂模塊的 PELT 方法要少得多。
在圖 (8) 中繪制帶有變點的時間序列。
def plot_change_points(ts,ts_change_loc):
plt.figure(figsize=(16,4))
plt.plot(ts)
for x in ts_change_loc:
plt.axvline(x,lw=2, color='red')
plot_change_points(ts1,ts_change_loc1)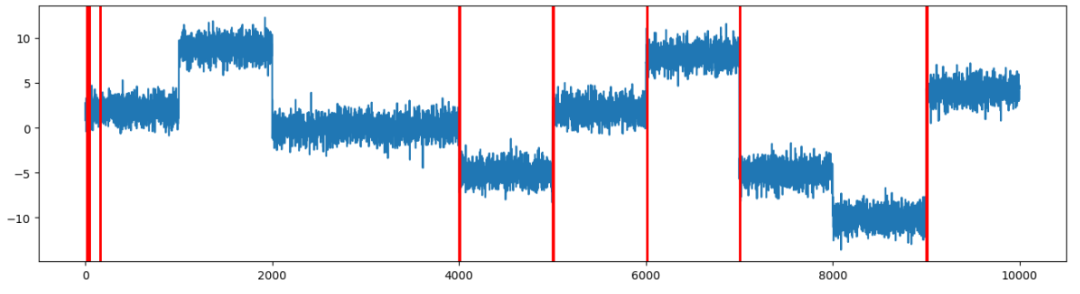 圖(8):SDAR 算法檢測到了恒定方差時間序列 10 個變點中的大多數變點
圖(8):SDAR 算法檢測到了恒定方差時間序列 10 個變點中的大多數變點
(2)變化方差
變化方差時間序列中的變點很難找到。如圖(9)所示,ts2 看起來像三到四個簇,而不是我們設計的十個簇。
ts_score2 = findChangePoints(ts2, r = 0.01, order = 3, smooth = 5)圖 (9) 顯示了第一張圖中的 ts2 和第二張圖中的變點分數。有三個高點。
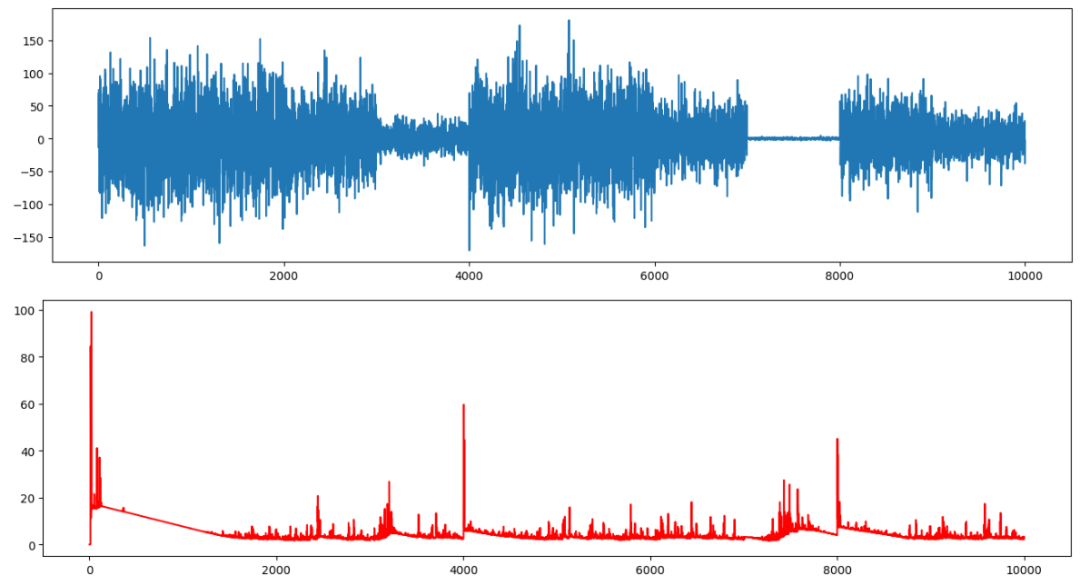 圖(9):變化方差時間序列的 SDAR 算法變點得分
圖(9):變化方差時間序列的 SDAR 算法變點得分
打印出前 20 名的位置。
ts_change_loc2 = pd.Series(ts_score2).nlargest(20)
ts_change_loc2 = ts_change_loc2.index
np.sort(ts_change_loc2)array([ 11, 12, 13, 19, 20, 21, 22, 80, 81, 107,
108, 117, 4003, 4004, 4010, 4011, 8000,
8001, 8007, 8008])*該方法確定了 1、4000、8000,但錯過了 1000、2000、3000、5000、6000、7000 和 9000 的變點。
plot_change_points(ts2,ts_change_loc2)如果我們直觀地觀察圖(10),就會發現有三四個聚類。SDAR 算法可以檢測到這些主要變點。
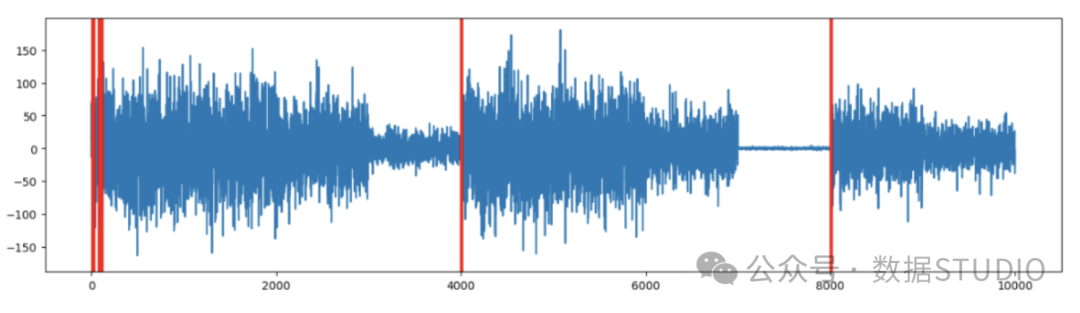 圖(10):SDAR 算法檢測變化方差時間序列的主要變點
圖(10):SDAR 算法檢測變化方差時間序列的主要變點












































