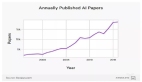
只需百行代碼,讓H100提速30%,斯坦福開源全新AI加速框架
AI 的快速發展,伴隨而來的是大計算量。這就自然而然的引出了一個問題:如何減少 AI 對計算的需求,并提高現有 AI 計算效率。
為了回答這一問題,來自斯坦福的研究者在博客《GPUs Go Brrr》中給出了答案。
 圖片
圖片
博客地址:https://hazyresearch.stanford.edu/blog/2024-05-12-tk
文章主要專注于兩個問題:一是硬件真正需要什么?二是如何滿足硬件需求?
文章用大量篇幅討論了如何讓 GPU 更快的運行,并發布了一個庫 ThunderKittens,用戶可以很容易地在 CUDA 上編寫快速的深度學習內核。其具有以下特點:
簡單,ThunderKittens 寫起來非常簡單。可擴展性,如果用戶需要 ThunderKittens 無法提供的功能,可以進行功能擴展。 速度快。
 圖片
圖片
GitHub 鏈接:https://github.com/HazyResearch/ThunderKittens
ThunderKittens 使得一些棘手的事情變得非常簡單,從而在現代硬件上實現了非常高的利用率。項目中,作者用 ThunderKittens 編寫了一個 RTX 4090 簡單的 FlashAttention-2 內核,代碼總共有 58 行代碼(不包括空格),結果顯示,ThunderKittens 在 RTX 4090 上實現了大約 122 TFLOP(理論最大值的 74%)。此外,內核程序只有 100 行的情況下,ThunderKittens 在 H100 上的性能比 FlashAttention-2 高出約 30%。
英偉達 H100 有些小怪癖
該研究重點關注 NVIDIA H100,不過所介紹的內容也適用于其他 GPU。
 圖片
圖片
H100 SXM GPU 包含:
80 GB HBM3,帶寬為 3 TB/s(實際上帶寬會少一些);50 MB 二級緩存,帶寬 12 TB/s,在 GPU 上分成兩個 25MB 的部分,通過 crossbar 連接;132 個流多處理器 (SM,streaming multiprocessors)。
除了上述這些,H100 SXM GPU 還有很多可關注的東西,例如內存控制器、指令緩存等。
研究者表示保持張量核心的運行流暢并不容易。他們發現了一些 AI 硬件上的怪癖,這些怪癖中的很多內容也適用于非 H100 GPU,但 H100 尤其棘手。(相比之下,RTX 4090 則非常容易使用),這些怪癖包括:
WGMMA 指令是必需的,但使用起來也非常令人惱火;共享內存實際上并沒有那么快,并且需要非常小心;地址生成成本很高;占用率仍然有幫助,寄存器通常是關鍵資源。
 圖片
圖片
文章進一步描述了 GPU 這些怪癖的具體內容。
WGMMA 指令令人惱火
H100 有一組新指令,稱為「warp group matrix multiply accumulate,WGMMA」(PTX 中的 wgmma.mma_async,或 SASS 中的 HGMMA/IGMMA/QGMMA/BGMMA)。以前的 GPU 上可用的張量核心指令是 wmma.mma.sync 和 mma.sync 。通過這些指令,SM 單個象限上的 32 個線程將同步地將其數據塊饋送到張量核心并等待結果。
不同的是,wgmma.mma_async 指令并非如此,128 個連續線程(分布在 SM 的所有象限中)協作同步,并直接從共享內存(也可以選擇寄存器)異步啟動矩陣乘法。
在基準測試中,研究團隊發現這些指令對于提取 H100 的完整計算是必要的。如果沒有它們,GPU 的峰值利用率似乎只能達到峰值利用率的 63% 左右。
 圖片
圖片
共享內存
共享內存的單次訪問延遲約為 30 個周期,這聽起來似乎不算多,但在這段時間內,SM 的張量核心幾乎可以完成兩個完整的 32x32 矩陣乘法運算。
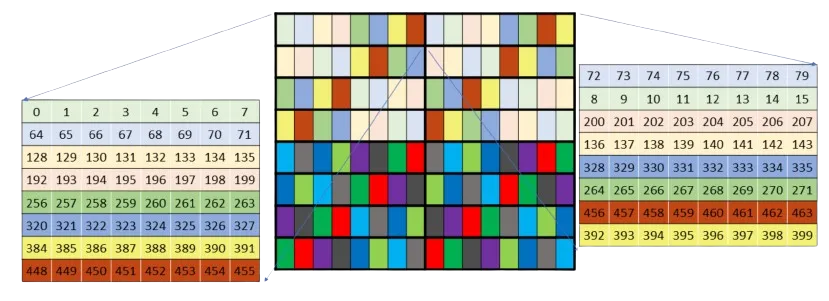
共享內存處理起來有些棘手,因為它被存儲(banked)在 32 個獨立的內存存儲中。如果不小心,這可能會導致所謂的 bank 沖突,即同一內存 bank 被要求同時提供多個不同的內存片段,導致請求被串行化,這可能會不成比例地減慢內核的速度 - 而 wgmma 和 mma 指令所需的寄存器布局會受到這些 bank 沖突的影響。解決方法是使用各種交錯模式重新排列共享內存,以避免這些沖突。
地址生成
H100 其中一個特點是張量核心和內存都足夠快,以至于僅僅生成用于獲取數據的內存地址就占據了芯片資源的相當一部分。
NVIDIA 似乎已經意識到了這一點,因為他們賦予了 GPU 張量內存加速器(或稱之為 TMA)。TMA 允許用戶在全局和共享內存中指定多維張量布局,這節省了所有的地址生成成本,并且還使得構建 pipeline 更加容易。
研究團隊還發現 TMA 和 wgmma.mma_async 一樣,在實現 H100 的全部潛力方面是完全不可或缺的。
占用
在某些方面,與前幾代硬件相比,H100 對占用率的依賴程度較低。NVIDIA 確實在設計 GPU 時考慮了占用率。雖然對于 H100 來說,占用率只能說有用,但作用不大。研究者發現在 A100 和 RTX 4090 上它變得越來越重要。
ThunderKittens
那么,如何才能更輕松地編寫內核,同時仍兼具硬件的全部功能?
研究團隊設計了一個嵌入 CUDA 中的 DSL,被命名為 ThunderKittens。
 圖片
圖片
ThunderKittens 旨在盡可能簡單,并包含四種模板類型:
寄存器 tile—— 寄存器文件中的 2D 張量。寄存器向量 —— 寄存器文件中的 1D 張量。共享 tile—— 共享內存中的 2D 張量。共享向量 —— 共享內存中的 1D 張量。
tile 通過高度、寬度和布局進行參數化,寄存器向量由長度和布局參數化,共享向量僅由長度參數化。這樣通常不會遭受 bank 沖突的困擾。
研究團隊還提供了一些必要操作:
初始化,如將共享向量清零
一元運算,如 exp二元運算,如 mul行 / 列操作,如 row_sum
該研究給出了一個用 ThunderKittens 編寫的,用于 RTX 4090 的簡單前向 flash attention 內核:
#define NUM_WORKERS 16 // This kernel uses 16 workers in parallel per block, to help issue instructions more quickly.
using namespace kittens; // this kernel only handles headdim=64 for simplicity. Also n should be a multiple of 256 here.
__global__ void attend_ker64(int n, const bf16* __restrict__ __q__, const bf16* __restrict__ __k__, const bf16* __restrict__ __v__, bf16* __o__) {
auto warpid = kittens::warpid();
auto block_start = blockIdx.x*(n*64);
const bf16 *_q = __q__ + block_start, *_k = __k__ + block_start, *_v = __v__ + block_start;
bf16 *_o = __o__ + block_start;
extern __shared__ alignment_dummy __shm[]; // this is the CUDA shared memory
shared_allocator al((int*)&__shm[0]);
// K and V live in shared memory -- this is about all that will fit.
st_bf_1x4<ducks::st_layout::swizzle> (&k_smem)[NUM_WORKERS] = al.allocate<st_bf_1x4<ducks::st_layout::swizzle>, NUM_WORKERS>();
st_bf_1x4<ducks::st_layout::swizzle> (&v_smem)[NUM_WORKERS] = al.allocate<st_bf_1x4<ducks::st_layout::swizzle>, NUM_WORKERS>();
// Initialize all of the register tiles.
rt_bf_1x4<> q_reg, k_reg, v_reg; // v_reg need to be swapped into col_l
rt_fl_1x1<> att_block;
rt_bf_1x1<> att_block_mma;
rt_fl_1x4<> o_reg;
rt_fl_1x1<>::col_vec max_vec_last, max_vec; // these are column vectors for the attention block
rt_fl_1x1<>::col_vec norm_vec_last, norm_vec; // these are column vectors for the attention block
int qo_blocks = n / (q_reg.rows*NUM_WORKERS), kv_blocks = n / (q_reg.rows*NUM_WORKERS);
for(auto q_blk = 0; q_blk < qo_blocks; q_blk++) {
// each warp loads its own Q tile of 16x64, and then multiplies by 1/sqrt(d)
load(q_reg, _q + (q_blk*NUM_WORKERS + warpid)*q_reg.num_elements, q_reg.cols);
mul(q_reg, q_reg, __float2bfloat16(0.125f)); // temperature adjustment
// zero flash attention L, M, and O registers.
neg_infty(max_vec); // zero registers for the Q chunk
zero(norm_vec);
zero(o_reg);
// iterate over k, v for these q's that have been loaded
for(auto kv_idx = 0; kv_idx < kv_blocks; kv_idx++) {
// each warp loads its own chunk of k, v into shared memory
load(v_smem[warpid], _v + (kv_idx*NUM_WORKERS + warpid)*q_reg.num_elements, q_reg.cols);
load(k_smem[warpid], _k + (kv_idx*NUM_WORKERS + warpid)*q_reg.num_elements, q_reg.cols);
__syncthreads(); // we need to make sure all memory is loaded before we can begin the compute phase
// now each warp goes through all of the subtiles, loads them, and then does the flash attention internal alg.
for(int subtile = 0; subtile < NUM_WORKERS; subtile++) {
load(k_reg, k_smem[subtile]); // load k from shared into registers
zero(att_block); // zero 16x16 attention tile
mma_ABt(att_block, q_reg, k_reg, att_block); // Q@K.T
copy(norm_vec_last, norm_vec);
copy(max_vec_last, max_vec);
row_max(max_vec, att_block, max_vec); // accumulate onto the max_vec
sub_row(att_block, att_block, max_vec); // subtract max from attention -- now all <=0
exp(att_block, att_block); // exponentiate the block in-place.
sub(max_vec_last, max_vec_last, max_vec); // subtract new max from old max to find the new normalization.
exp(max_vec_last, max_vec_last); // exponentiate this vector -- this is what we need to normalize by.
mul(norm_vec, norm_vec, max_vec_last); // and the norm vec is now normalized.
row_sum(norm_vec, att_block, norm_vec); // accumulate the new attention block onto the now-rescaled norm_vec
div_row(att_block, att_block, norm_vec); // now the attention block is correctly normalized
mul(norm_vec_last, norm_vec_last, max_vec_last); // normalize the previous norm vec according to the new max
div(norm_vec_last, norm_vec_last, norm_vec); // normalize the previous norm vec according to the new norm
copy(att_block_mma, att_block); // convert to bf16 for mma_AB
load(v_reg, v_smem[subtile]); // load v from shared into registers.
rt_bf_1x4<ducks::rt_layout::col> &v_reg_col = swap_layout_inplace(v_reg); // this is a reference and the call has invalidated v_reg
mul_row(o_reg, o_reg, norm_vec_last); // normalize o_reg in advance of mma_AB'ing onto it
mma_AB(o_reg, att_block_mma, v_reg_col, o_reg); // mfma onto o_reg with the local attention@V matmul.
}
__syncthreads(); // we need to make sure all warps are done before we can start loading the next kv chunk
}
store(_o + (q_blk*NUM_WORKERS + warpid)*q_reg.num_elements, o_reg, q_reg.cols); // write out o. compiler has an issue with register usage if d is made constexpr q_reg.rows :/
}
}總共大約有 60 行 CUDA 代碼,硬件利用率為 75%,雖然非常密集,但大部分復雜性在于算法,而不是混合模式或寄存器布局。
TMA、WGMMA、swizzling 模式和描述符的復雜度又如何呢?如下是用 ThunderKittens 編寫的, H100 的 FlashAttention-2 前向傳遞:
template<int D>
__global__ __launch_bounds__((NUM_WORKERS)*kittens::WARP_THREADS, 2)
void fwd_attend_ker_dim(int N, const CUtensorMap* tma_q, const CUtensorMap* tma_k, const CUtensorMap* tma_v, CUtensorMap* tma_o) {
extern __shared__ int __shm[]; // this is the CUDA shared memory
tma_swizzle_allocator al((int*)&__shm[0]);
constexpr int tile_width = fwd_attend_ker_tile_dims<D>::tile_width; // constants
constexpr int qo_height = fwd_attend_ker_tile_dims<D>::qo_height;
constexpr int kv_height = fwd_attend_ker_tile_dims<D>::kv_height;
st_bf<qo_height, tile_width, layout_q> (&q_smem) [NUM_WARPGROUPS] = al.allocate<st_bf<qo_height, tile_width, layout_q>, NUM_WARPGROUPS>();
st_bf<kv_height, tile_width, layout_k> (&k_smem)[2][NUM_WORKERS_KV] = al.allocate<st_bf<kv_height, tile_width, layout_k>, 2, NUM_WORKERS_KV>();
st_bf<kv_height, tile_width, layout_v> (&v_smem)[2][NUM_WORKERS_KV] = al.allocate<st_bf<kv_height, tile_width, layout_v>, 2, NUM_WORKERS_KV>();
int tic = 0, toc = 1;
rt_fl<1, kv_height> att_block;
rt_bf<1, kv_height> att_block_mma;
rt_fl<1, qo_height> o_prev;
col_vec<rt_fl<1, kv_height>> max_vec_last, max_vec;
col_vec<rt_fl<1, kv_height>> norm_vec_last, norm_vec;
int warpid = kittens::warpid();
int warpgroupid = warpid/kittens::WARPGROUP_WARPS;
int kv_blocks = N / (NUM_WORKERS_KV*k_smem[0][0].rows);
__shared__ uint64_t qsmem_barrier, kvsmem_barrier;//, vsmem_barrier;
int q_phasebit = 0;
int kv_phasebit = 0;
if (threadIdx.x == 0) {
tma::init_barrier<st_bf<qo_height, tile_width, layout_q>, NUM_WARPGROUPS>(qsmem_barrier, 1);
tma::init_barrier<st_bf<kv_height, tile_width, layout_k>, NUM_WORKERS_KV*2>(kvsmem_barrier, 1);
}
if (warpid == 0) {
for (int wg = 0; wg < NUM_WORKERS/kittens::WARPGROUP_WARPS; wg++) { // load q
int tile_idx = (blockIdx.y * NUM_WARPGROUPS * gridDim.x) + (blockIdx.x * NUM_WARPGROUPS) + wg;
tma::load_async((q_smem[wg]), tma_q, qsmem_barrier, tile_idx);
}
for (int w = 0; w < NUM_WORKERS_KV; w++) { // load k, v
int tile_idx = (blockIdx.y * NUM_WORKERS_KV * kv_blocks) + (0 * NUM_WORKERS_KV) + w;
tma::load_async((k_smem[tic][w]), tma_k, kvsmem_barrier, tile_idx);
tma::load_async((v_smem[tic][w]), tma_v, kvsmem_barrier, tile_idx);
}
}
neg_infty(max_vec); // zero registers for the Q chunk
zero(norm_vec);
zero(o_prev);
__syncthreads();
tma::arrive_and_wait(qsmem_barrier, q_phasebit);
q_phasebit ^= 1;
if constexpr (D == 64) { warpgroup::mul(q_smem[warpgroupid], q_smem[warpgroupid], __float2bfloat16(0.125f)); }
else { warpgroup::mul(q_smem[warpgroupid], q_smem[warpgroupid], __float2bfloat16(0.08838834764f)); }
for (auto kv_idx = 0; kv_idx < kv_blocks; kv_idx++, tic ^= 1, toc ^= 1) {
tma::arrive_and_wait(kvsmem_barrier, kv_phasebit);
kv_phasebit ^= 1;
__syncthreads();
if (warpid == 0) {
tma::set_bytes(kvsmem_barrier, 2 * NUM_WORKERS_KV * k_smem[0][0].num_elements * sizeof(bf16));
if (kv_idx + 1 < kv_blocks) {
for (int w = 0; w < NUM_WORKERS_KV; w++) {
int tile_idx = (blockIdx.y * NUM_WORKERS_KV * kv_blocks) + ((kv_idx + 1) * NUM_WORKERS_KV) + w;
tma::load_async((k_smem[toc][w]), tma_k, kvsmem_barrier, tile_idx);
tma::load_async((v_smem[toc][w]), tma_v, kvsmem_barrier, tile_idx);
}
}
}
warpgroup::mma_fence(att_block);
warpgroup::mm_ABt(att_block, q_smem[warpgroupid], k_smem[tic][0]);
warpgroup::mma_commit_group();
copy(norm_vec_last, norm_vec);
copy(max_vec_last, max_vec);
warpgroup::mma_async_wait();
row_max(max_vec, att_block, max_vec); // accumulate onto the max_vec
sub_row(att_block, att_block, max_vec);
exp(att_block, att_block);
sub(max_vec_last, max_vec_last, max_vec);
exp(max_vec_last, max_vec_last);
mul(norm_vec, norm_vec, max_vec_last);
row_sum(norm_vec, att_block, norm_vec); // accumulate onto the norm_vec
div_row(att_block, att_block, norm_vec);
mul(norm_vec_last, norm_vec_last, max_vec_last);
div(norm_vec_last, norm_vec_last, norm_vec);
copy(att_block_mma, att_block); // convert to bf16 for mma
mul_row(o_prev, o_prev, norm_vec_last); // normalize o_prev in advance of mma'ing onto it
warpgroup::mma_fence(o_prev);
warpgroup::mma_AB(o_prev, att_block_mma, v_smem[tic][0]);
warpgroup::mma_commit_group();
}
auto (*o_smem) = reinterpret_cast<st_bf<qo_height, tile_width, layout_o>(*)>(q_smem); // reuse q memory
warpgroup::store(o_smem[warpgroupid], o_prev);
__syncthreads();
if (warpid % 4 == 0) { // store o
int tile_idx = (blockIdx.y * NUM_WARPGROUPS * gridDim.x) + (blockIdx.x * NUM_WARPGROUPS) + warpgroupid;
tma::store_async(tma_o, (o_smem[warpgroupid]), tile_idx);
tma::store_commit_group();
}
tma::store_async_wait();
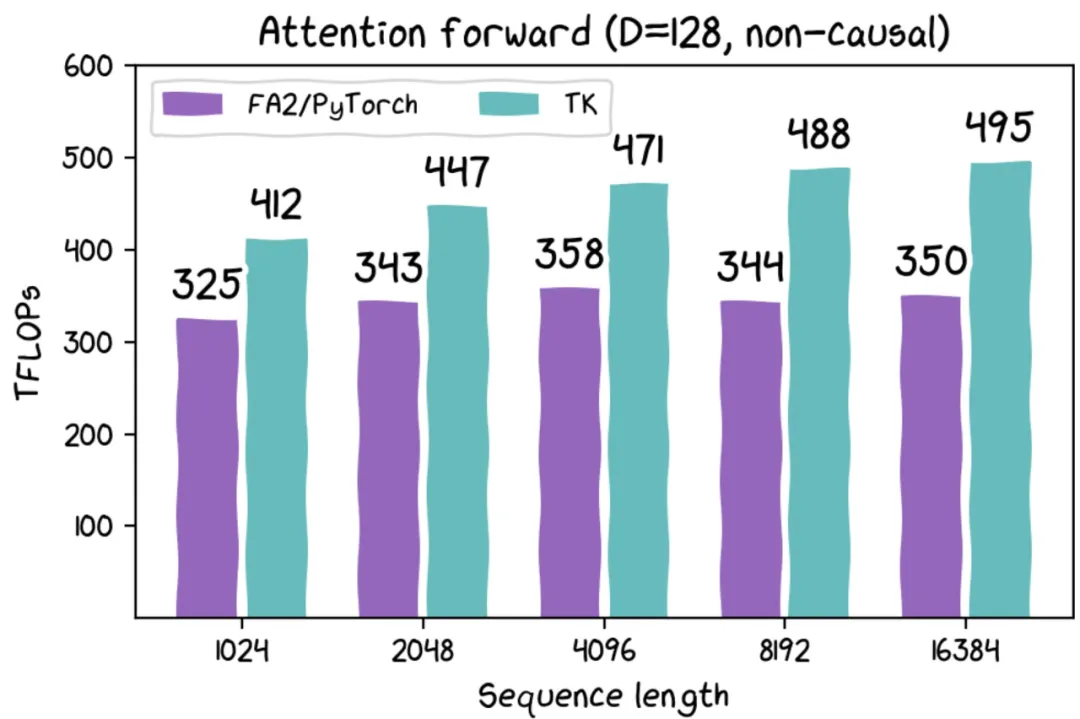
}這個內核只有 100 行代碼,它在 H100 上的性能比 FlashAttention-2 高出約 30%。ThunderKittens 負責 wrap up 布局和指令,并提供一個可以在 GPU 上使用的 mini-pytorch。
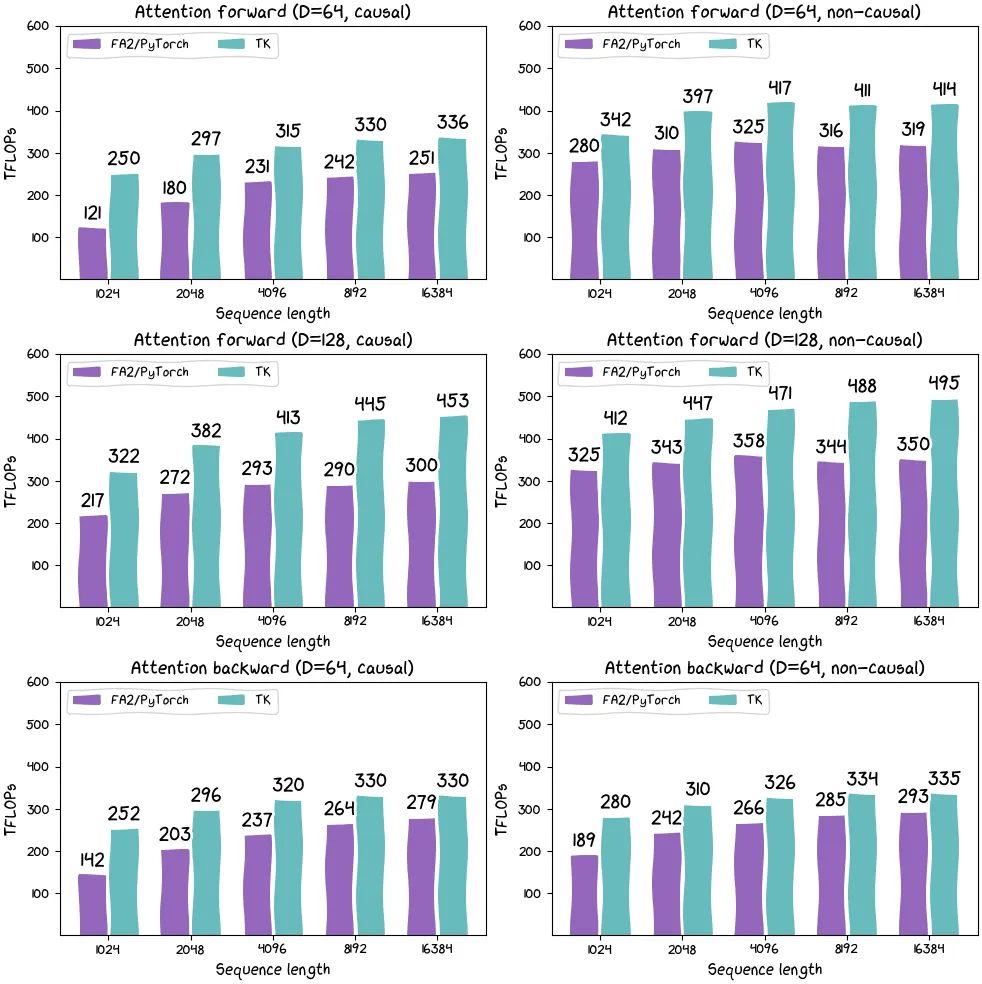 圖片
圖片
H100 SXM 上各種配置的 FlashAttention-2(Pytorch)與 ThunderKittens 的比較。
此外,研究團隊還發布了基于線性注意力的內核和其他架構。基于線性注意力內核的運行速度為 215 TFLOP(如果考慮算法中固有的重計算,則運行速度超過 300 TFLOP)。
雖然理論上線性注意力更高效,但從實踐經驗來看,線性注意力在硬件上的效率大大降低。因此,ThunderKittens 有望開辟廣泛的高吞吐量應用。
圖片使用 ThunderKittens 可以非常快地實現線性注意力。
tile 看起來是個好點子
在研究團隊看來,ThunderKittens 之所以運行良好,是因為它不會試圖做所有事情。CUDA 確實比 ThunderKittens 更有表現力,而 ThunderKittens 又小又簡單。
不過,ThunderKittens 具有很好的抽象能力,它具有小的 tile,這與 AI 和硬件的發展相匹配。ThunderKittens 不支持任何少于 16 的維數。但在研究團隊看來,這一點并不重要,尤其對于硬件而言。如果你的矩陣乘法小于 16x16,你確定自己做的還是 AI 嗎?
從哲學的視角來看,研究團隊認為框架遷移是合理的。「寄存器」當然不應該像舊 CPU 那樣的 32 位。CUDA 使用的 1024 位寬向量寄存器無疑朝著正確方向邁出了一步。但對研究團隊而言,「寄存器」是 16x16 的數據 tile。他們認為 AI 想要這樣,它仍然只是矩陣乘法、規約和重塑。當然硬件也想要這樣,小的矩陣乘法尋求硬件支持,而不僅僅是 systolic mma。
實際上,從更廣泛的視角來看,研究團隊認為應該圍繞硬件的良好映射來重新調整 AI 思路。比如,循環狀態應該有多大?SM 能夠容納多大尺寸?計算密度是多少?這些都不亞于硬件的要求。
研究團隊表示,這項工作未來的一個重要方向是利用他們對硬件的了解來幫助設計與硬件相匹配的 AI。
最后,AMD 硬件上適配的 ThunderKittens 也將很快推出。