每個(gè)程序員都應(yīng)該了解的硬件知識(shí)

作者：騰訊技術(shù)工程 2024-04-10 12:36:41

本文旨在通過多個(gè)可運(yùn)行的 benchmark 介紹常見的優(yōu)化細(xì)節(jié)以及與之相關(guān)的硬件知識(shí)，為讀者建立一個(gè)簡單、有效的硬件心智模型。

在追求高效代碼的路上，我們不可避免地會(huì)遇到代碼的性能瓶頸。為了了解、解釋一段代碼為什么低效，并嘗試改進(jìn)低效的代碼，我們總是要了解硬件的工作原理。于是，我們可能會(huì)嘗試搜索有關(guān)某個(gè)架構(gòu)的介紹、一些優(yōu)化指南或者閱讀一些計(jì)算機(jī)科學(xué)的教科書（如：計(jì)算機(jī)組成原理）。但以上的內(nèi)容可能都太過繁瑣、細(xì)節(jié)太多，在閱讀的過程中，我們可能會(huì)迷失在紛繁的細(xì)節(jié)中，沒法很好地將知識(shí)運(yùn)用到實(shí)踐中。

一、Cache

首先要介紹的就是緩存 cache 。我們先來看一個(gè)引自 CSAPP 的經(jīng)典例子：

pub fn row_major_traversal(arr: &mut Vec<Vec<usize>>) {
    let n = arr.len();
    for i in 0..n {
        assert!(arr[i].len() == n);
        for j in 0..n {
            arr[i][j] += j;
        }
    }
}

pub fn column_major_traversal(arr: &mut Vec<Vec<usize>>) {
    let n = arr.len();
    for i in 0..n {
        assert!(arr[i].len() == n);
        for j in 0..n {
            arr[j][i] += j;
        }
    }
}

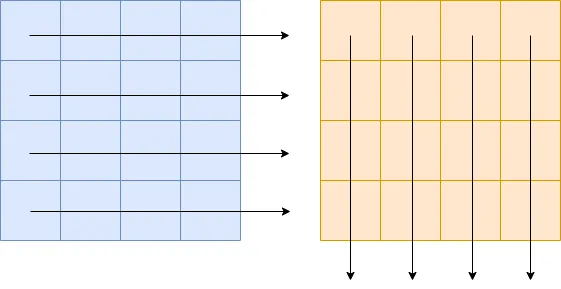
在上面兩個(gè)例子中，分別按行、按列迭代同樣大小的二維數(shù)組。

我們對這兩個(gè)函數(shù)進(jìn)行 benchmark：

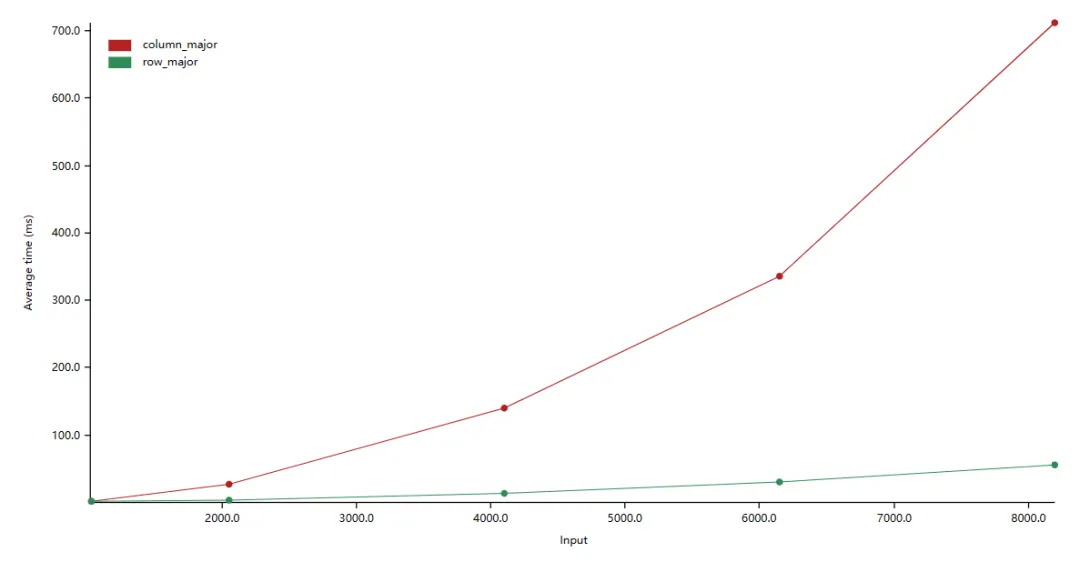
在上圖中，縱軸是平均耗時(shí)，橫軸是數(shù)組大小（如：2000.0 表示數(shù)組大小為：2000 x 2000）。我們看到按行迭代數(shù)組比按列迭代的效率高約 10 倍。

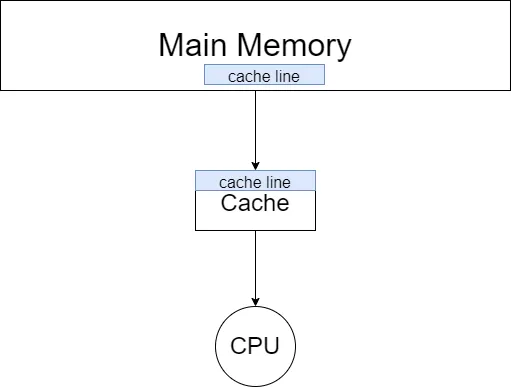
在現(xiàn)代的存儲(chǔ)架構(gòu)中，cpu 和主存之間是 cache 。cpu 中的寄存器、高速緩存、內(nèi)存三者的數(shù)據(jù)讀寫速度越來越慢。

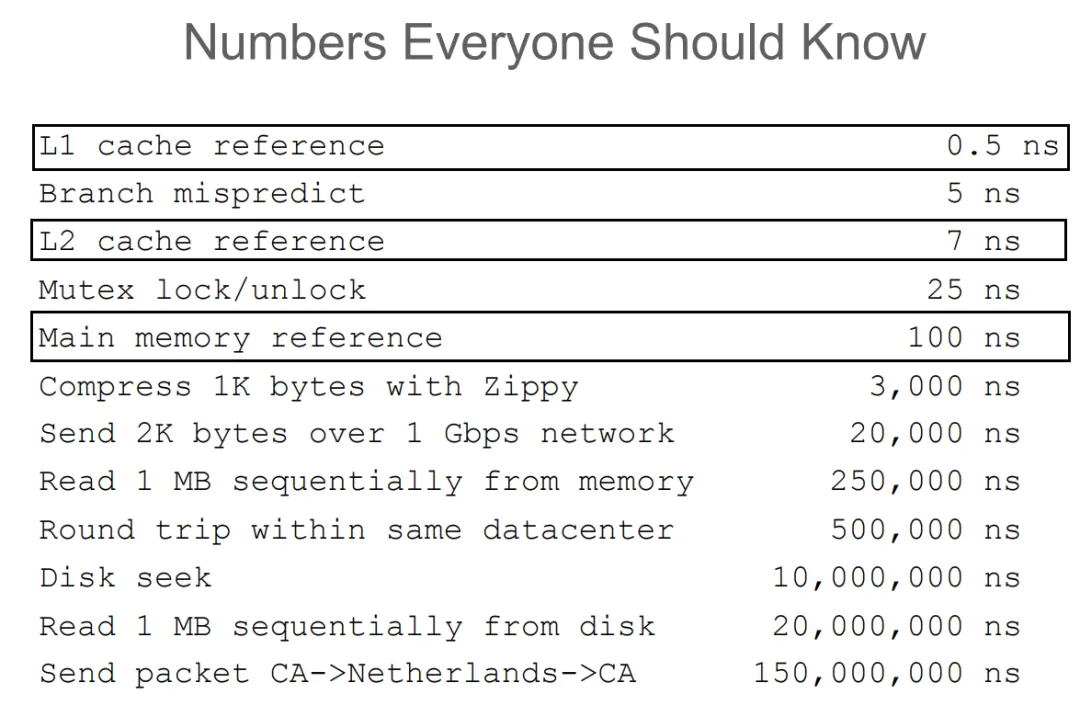
而當(dāng) cpu 讀取一個(gè)數(shù)據(jù)的時(shí)候，會(huì)先嘗試從 cache 中讀取。如果發(fā)生 cache miss 的時(shí)候，才會(huì)將數(shù)據(jù)從主存中加載到 cache 中再讀取。而值得注意的是，cpu 每一次的讀取都是以 cache line 為單位的。也就是說，cpu 在讀取一個(gè)數(shù)據(jù)的時(shí)候，也會(huì)將該數(shù)據(jù)相鄰的、一個(gè) cache line 內(nèi)的數(shù)據(jù)也加載到 cache 中。而二維數(shù)組在內(nèi)存中是按行排布的，換句話說，數(shù)組中相鄰的兩行是首尾相連排列的。所以在讀取 arr[i] 的時(shí)候，arr[i + 1] 、arr[i + 2] 等相鄰的數(shù)組元素也會(huì)被加載到 cache 中，而當(dāng)下一次迭代中，需要讀取數(shù)組元素 arr[i + 1] 時(shí)，就能直接從 cache 中取出，速度非常快。而因?yàn)橐粤凶x取數(shù)組時(shí)，arr[i][j] 和 arr[i + 1][j] 在內(nèi)存中的位置就不再是緊密相連，而是相距一個(gè)數(shù)組行大小。這也導(dǎo)致了在讀取 arr[i][j] 時(shí)，arr[i + 1][j] 并沒有被加載到 cache 中。在下一次迭代時(shí)就會(huì)發(fā)生 cache miss 也就導(dǎo)致讀取速度大幅下降。

1.prefetcher

如果我們不再是按某種順序，而是隨機(jī)地遍歷數(shù)組，結(jié)果又會(huì)如何呢？

pub fn row_major_traversal(arr: &mut Vec<Vec<usize>>) {
    let n = arr.len();
    for i in 0..n {
        assert!(arr[i].len() == n);
        let ri: usize = rand::random();
        std::intrinsics::black_box(ri);
        for j in 0..n {
            arr[i][j] += j;
        }
    }
}

pub fn column_major_traversal(arr: &mut Vec<Vec<usize>>) {
    let n = arr.len();
    for i in 0..n {
        assert!(arr[i].len() == n);
        let ri: usize = rand::random();
        std::intrinsics::black_box(ri);
        for j in 0..n {
            arr[j][i] += j;
        }
    }
}

pub fn random_access(arr: &mut Vec<Vec<usize>>) {
    let n = arr.len();
    for i in 0..n {
        assert!(arr[i].len() == n);
        for j in 0..n {
            let ri: usize = rand::random();
            arr[j][ri % n] += j;
        }
    }
}

理論上來說，隨機(jī)遍歷和按列遍歷都會(huì)導(dǎo)致頻繁地 cache miss ，所以兩者的效率應(yīng)該是相近的。接下來，我們進(jìn)行 benchmark：

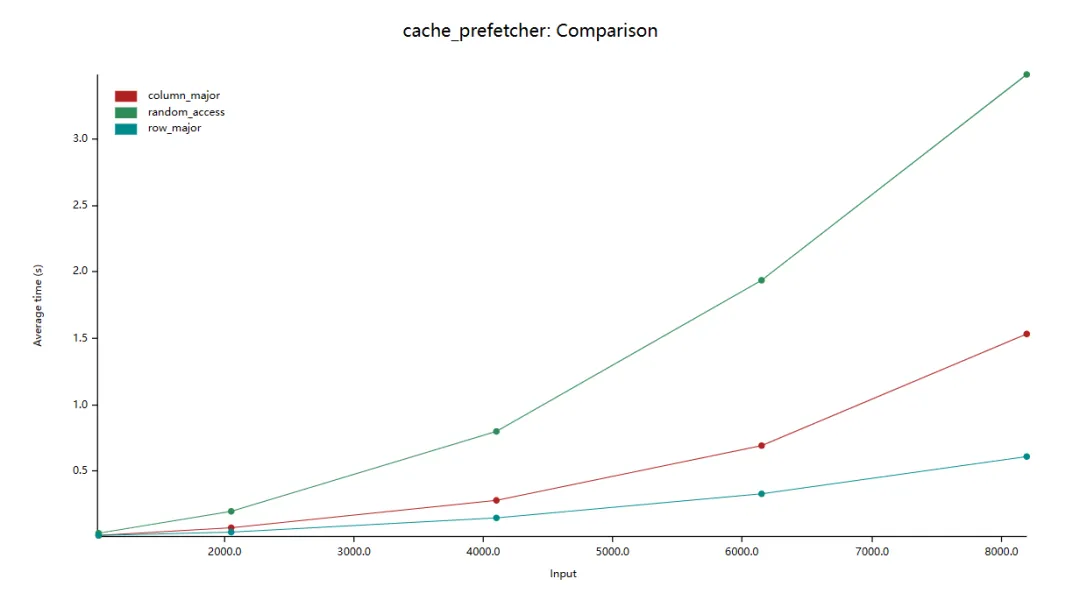
可以看到，random_access 比 column_major 的效率還要低了 2 倍。原因是，在 cache 和 cpu 間還有 prefetcher

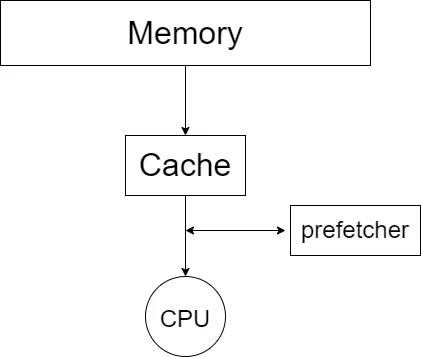
我們可以參考維基百科上的資料：

Cache prefetching can be accomplished either by hardware or by software.
Hardware based prefetching is typically accomplished by having a dedicated hardware mechanism in the processor that watches the stream of instructions or data being requested by the executing program, recognizes the next few elements that the program might need based on this stream and prefetches into the processor's cache.
Software based prefetching is typically accomplished by having the compiler analyze the code and insert additional "prefetch" instructions in the program during compilation itself.

而 random_access 會(huì)讓 prefetching 的機(jī)制失效，使得運(yùn)行效率進(jìn)一步下降。

2.cache associativity

如果我們按照不同的步長迭代一個(gè)數(shù)組會(huì)怎么樣呢？

pub fn iter_with_step(arr: &mut Vec<usize>, step: usize) {
    let n = arr.len();
    let mut i = 0;
    for _ in 0..1000000 {
        unsafe { arr.get_unchecked_mut(i).add_assign(1); }
        i = (i + step) % n;
    }
}

steps 為：

let steps = [
    1, 
    2, 
    4, 
    7, 8, 9,
    15, 16, 17,
    31, 32, 33,
    61, 64, 67,
    125, 128, 131,
    253, 256, 259, 
    509, 512, 515, 
    1019, 1024, 1031
];

我們進(jìn)行測試：

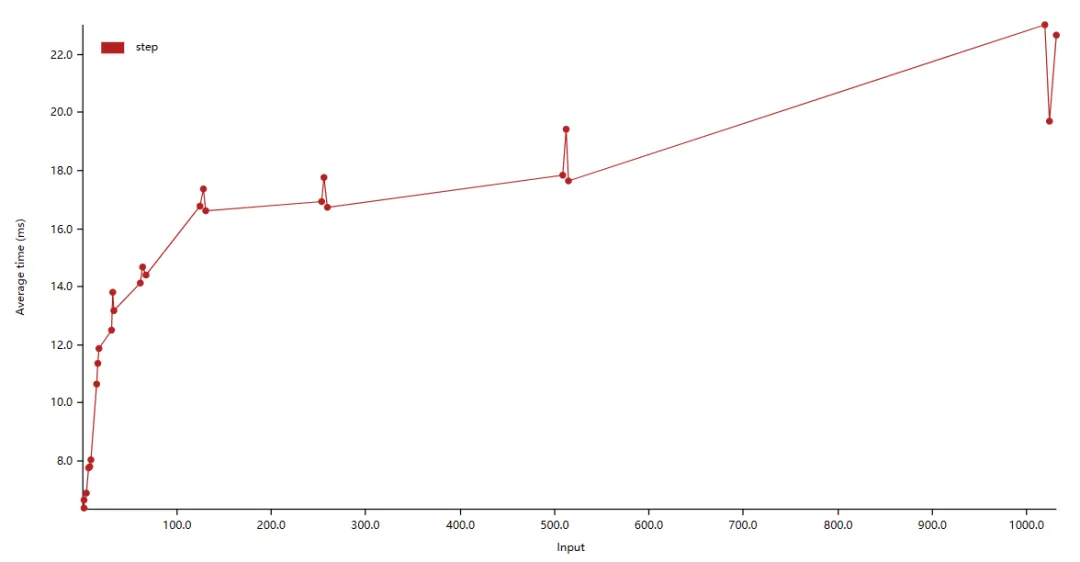
可以看見當(dāng) step 為 2 的冪次時(shí)，都會(huì)有一個(gè)運(yùn)行時(shí)間的突起，一個(gè)性能的毛刺。這是為什么呢？要回答這個(gè)問題，我們需要溫習(xí)一些計(jì)組知識(shí)。

cache 的大小是要遠(yuǎn)小于主存的。這就意味著我們需要通過某種方式將主存的不同位置映射到緩存中。一般來說，共有 3 種不同的映射方式。

(1) 全相聯(lián)映射

全相聯(lián)映射允許主存中的行可以映射到緩存中的任意一行。這種映射方式靈活性很高，但會(huì)使得緩存的查找速度下降。

(2) 直接映射

直接映射則規(guī)定主存中的某一行只能映射到緩存中的特定行。這種映射方式查找速度高，但靈活性很低，會(huì)經(jīng)常導(dǎo)致緩存沖突，從而導(dǎo)致頻繁 cache miss 。

(3) 組相聯(lián)映射

組相聯(lián)映射則嘗試吸收前兩者的優(yōu)點(diǎn)，將緩存中的緩存行分組，主存中某一行只能映射到特定的一組，在組內(nèi)則采取全相聯(lián)的映射方式。如果一組之內(nèi)有 n 個(gè)緩存行，我們就稱這種映射方式為 n 路組相聯(lián)（n-way set associative）。

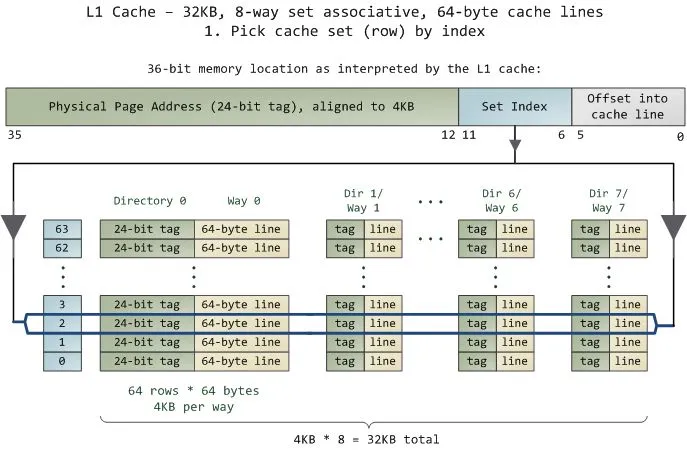
回到真實(shí)的 cpu 中，如：AMD Ryzen 7 4700u 。

我們可以看到，L1 cache 大小為 4 x 32 KB (128KB) ，采取 8 路組相聯(lián)，緩存行大小為 64 bytes 。也就是說，該緩存共有 4x32x1024 byte/64 byte = 2048 行，共分為 2048/8 = 256 組。也就是說，當(dāng)?shù)鷶?shù)組的步長為時(shí)，數(shù)據(jù)更可能會(huì)被分到同一個(gè)組內(nèi)，導(dǎo)致 cache miss 更加頻繁，從而導(dǎo)致效率下降。

（注：我的 cpu 是 intel i7-10750H ，算得的 L1 cache 的組數(shù)為 384 ，并不能很好地用理論解釋。）

3.false share

我們再來觀察一組 benchmark 。

use std::sync::atomic::{AtomicUsize, Ordering};
use std::thread;

fn increase(v: &AtomicUsize) {
    for _ in 0..10000 {
        v.fetch_add(1, Ordering::Relaxed);
    }
}

pub fn share() {
    let v = AtomicUsize::new(0);
    thread::scope(|s| {
        let ta = s.spawn(|| increase(&v));
        let tb = s.spawn(|| increase(&v));
        let tc = s.spawn(|| increase(&v));
        let td = s.spawn(|| increase(&v));

        ta.join().unwrap();
        tb.join().unwrap();
        tc.join().unwrap();
        td.join().unwrap();
    });
}

pub fn false_share() {
    let a = AtomicUsize::new(0);
    let b = AtomicUsize::new(0);
    let c = AtomicUsize::new(0);
    let d = AtomicUsize::new(0);

    thread::scope(|s| {
        let ta = s.spawn(|| increase(&a));
        let tb = s.spawn(|| increase(&b));
        let tc = s.spawn(|| increase(&c));
        let td = s.spawn(|| increase(&d));

        ta.join().unwrap();
        tb.join().unwrap();
        tc.join().unwrap();
        td.join().unwrap();
    });
}

在 share 函數(shù)中，四個(gè)線程同時(shí)競爭原子變量 v 。而在 false_share 函數(shù)中，四個(gè)線程分別操作不同的原子變量，理論上線程之間不會(huì)產(chǎn)生數(shù)據(jù)競爭，所以 false_share 的執(zhí)行效率應(yīng)該比 share 要高。但 benchmark 的結(jié)果卻出乎意料：

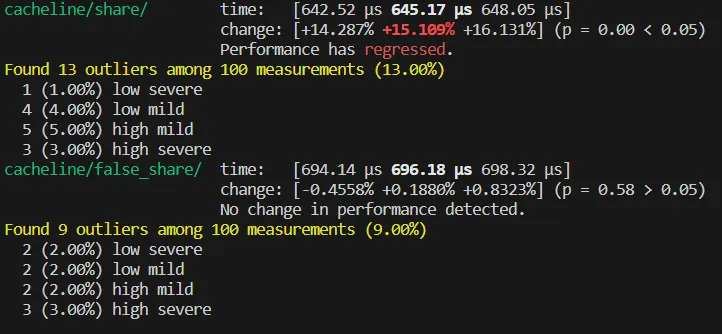
可以看到 false_share 比 share 的執(zhí)行效率還要低。

在前文中提到，cpu 在讀取數(shù)據(jù)時(shí)，是以一個(gè) cache line 大小為單位將數(shù)據(jù)從主存中加載到 cache 中的。在前文中提到，筆者機(jī)器的 cache line 大小為：64 bytes 。而 false_share 函數(shù)中，四個(gè)原子變量在棧中的排布可能是：

a, b, c, d 四個(gè)原子變量在同一個(gè) cache line 中，也就是說實(shí)際上四個(gè)線程實(shí)際上還是發(fā)生了競爭，產(chǎn)生了 false share 的現(xiàn)象。

那要如何解決這個(gè)問題呢？我們可以采用 #[repr(align(64))] （在不同的編程語言中又不同的寫法），告知編譯器將原子變量的內(nèi)存地址以一個(gè) cache line 大小對齊，從而避免四個(gè)原子變量位于同一個(gè) cache line 中。

fn increase_2(v: &AlignAtomicUsize) {
    for _ in 0..10000 {
        v.v.fetch_add(1, Ordering::Relaxed);
    }
}

#[repr(align(64))]
struct AlignAtomicUsize {
    v: AtomicUsize,
}

impl AlignAtomicUsize {
    pub fn new(val: usize) -> Self {
        Self { v: AtomicUsize::new(val) }
    }
}

pub fn non_share() {
    let a = AlignAtomicUsize::new(0);
    let b = AlignAtomicUsize::new(0);
    let c = AlignAtomicUsize::new(0);
    let d = AlignAtomicUsize::new(0);

    thread::scope(|s| {
        let ta = s.spawn(|| increase_2(&a));
        let tb = s.spawn(|| increase_2(&b));
        let tc = s.spawn(|| increase_2(&c));
        let td = s.spawn(|| increase_2(&d));

        ta.join().unwrap();
        tb.join().unwrap();
        tc.join().unwrap();
        td.join().unwrap();
    });
}

我們再次進(jìn)行 benchmark，這一次 benchmark 的結(jié)果就符合我們的預(yù)測了：

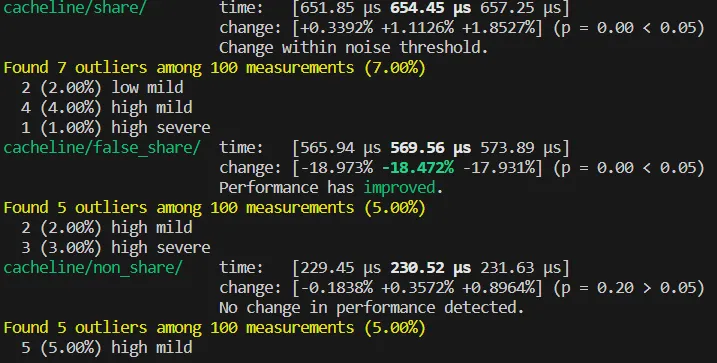
可以看見 non_share 相比前兩者，提升了近乎兩倍的效率。

二、pipeline

我們再看一個(gè) benchmark：

pub trait Get {
    fn get(&self) -> i32;
}

struct Foo { /* ... */ }
struct Bar { /* ... */ }

impl Get for Foo { /* ... */ }
impl Get for Bar { /* ... */ }

let mut arr: Vec<Box<dyn Get>> = vec![];
for _ in 0..10000 {
    arr.push(Box::new(Foo::new()));
}
for _ in 0..10000 {
    arr.push(Box::new(Bar::new()));
}

// 此時(shí)數(shù)組中元素的排列時(shí)有序的
arr.iter().filter(|v| v.get() > 0).count()

// 將數(shù)組打亂
arr.shuffle(&mut rand::thread_rng());

// 再次測試
arr.iter().filter(|v| v.get() > 0).count()

測試結(jié)果為：

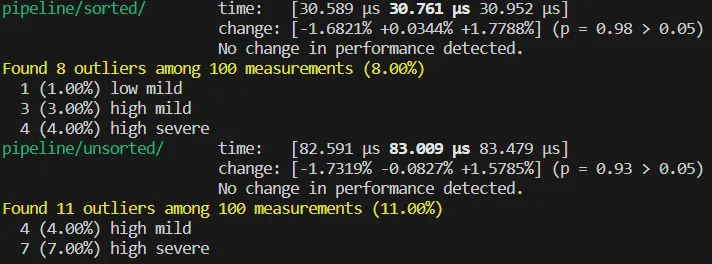
可以看見，sorted 和 unsorted 之間效率差約 2.67 倍。這是因?yàn)轭l繁的分支預(yù)測失敗導(dǎo)致的。

在CPU 中，每一條指令的執(zhí)行都會(huì)分為多個(gè)步驟，而現(xiàn)代計(jì)算機(jī)架構(gòu)中存在一個(gè)結(jié)構(gòu) pipeline 可以同時(shí)執(zhí)行處于不同執(zhí)行階段的指令。

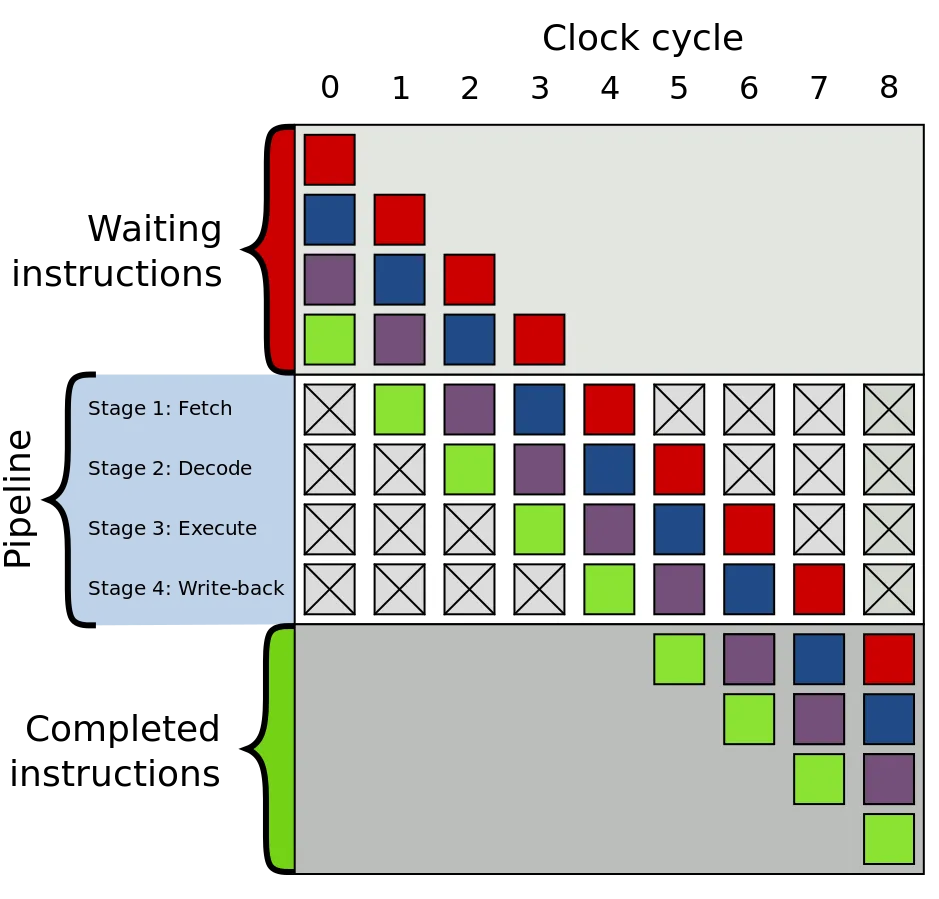
而 pipeline 要高效地工作，需要在執(zhí)行指令 A 時(shí)就將接下來要執(zhí)行的指令 B, C, D 等提前讀入。在一般的代碼中，pipeline 可以有效地工作，但遇到分支的時(shí)候，我們就遇到難題了：

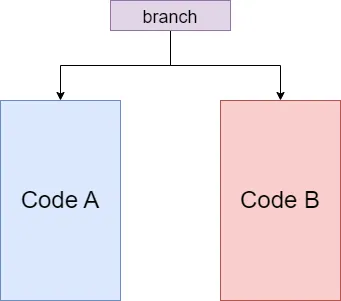
如圖，pipeline 應(yīng)該讀入 Code A 還是 Code B 呢？在執(zhí)行分支語句前，誰也不知道，CPU 也是。如果我們還想要 pipeline 高效工作的話，我們就只剩下一條路：猜。只要猜得足夠準(zhǔn)，我們的效率就能夠接近沒有分支的情況。“猜”這一步也有一個(gè)專業(yè)名詞——**流水線冒險(xiǎn)**。而現(xiàn)代計(jì)算機(jī)在編譯器配合以及一些算法的幫助下，某些分支（如下圖所示）的預(yù)測成功率可以高達(dá) 99% 。

分支預(yù)測失敗的代價(jià)是要付出代價(jià)的。首先，我們要清除 pipeline 中的指令，因?yàn)樗鼈儾皇墙酉聛硪獔?zhí)行的指令。其次，我們要將接下來要執(zhí)行的指令一一加載進(jìn) pipeline 。最后，指令經(jīng)過多個(gè)步驟被執(zhí)行。

在測試代碼中，我們打亂數(shù)組后，就會(huì)導(dǎo)致分支預(yù)測頻繁失敗，最終導(dǎo)致了執(zhí)行效率的下降。

三、數(shù)據(jù)依賴

我們再來看一段代碼：

pub fn dependent(a: &mut Vec<i32>, b: &mut Vec<i32>, c: &Vec<i32>) {
    assert!(a.len() == 100000);
    assert!(b.len() == 100000);
    assert!(c.len() == 100000);

    for i in 0..=99998 {
        a[i] += b[i];
        b[i + 1] += c[i];
    }
    a[9999] += b[9999];
}

pub fn independent(a: &mut Vec<i32>, b: &mut Vec<i32>, c: &Vec<i32>) {
    assert!(a.len() == 100000);
    assert!(b.len() == 100000);
    assert!(c.len() == 100000);

    a[0] += b[0];
    for i in 0..=99998 {
        b[i + 1] += c[i];
        a[i + 1] += b[i + 1];
    }
}

在這段代碼中，我們通過兩種不同的方式迭代數(shù)組，并最終達(dá)成一致的效果。我們畫出，數(shù)據(jù)流圖如下圖：

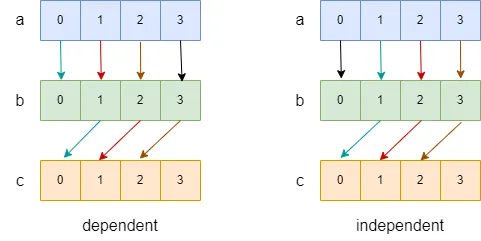
在上圖中，我們用箭頭表示依賴關(guān)系（a[0] -> b[0] 表示 a[0] 的結(jié)果依賴于 b[0] ），用黑色箭頭表示在循環(huán)外進(jìn)行的操作，用不同的顏色，表示不同迭代中的操作。我們可以看到，在 dependent 中，不同顏色的箭頭會(huì)出現(xiàn)在同一個(gè)數(shù)據(jù)流中，如：（a[1]->b[1]->c[0] 中就出現(xiàn)了紅色和藍(lán)色箭頭），這就意味著第 n + 1 次迭代會(huì)依賴于第 n 次迭代的結(jié)果，而 independent 中則沒有這種情況。

這會(huì)產(chǎn)生什么影響呢？我們來進(jìn)行測試：

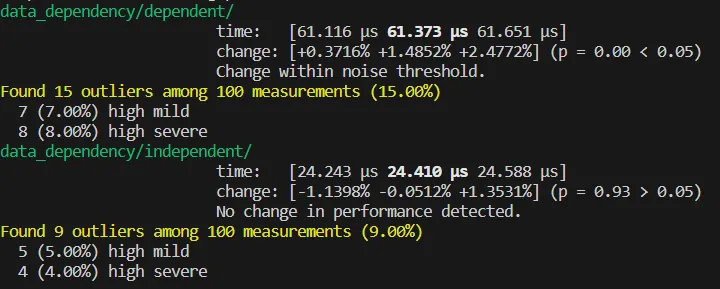
可以看到，出現(xiàn)了近 3 倍的效率差距。這有兩方面原因。

一是數(shù)據(jù)依賴會(huì)導(dǎo)致 pipeline 效率以及 cpu 指令級并行的效率變低。

二是這種迭代之間的依賴會(huì)阻止編譯器的向量化優(yōu)化。我們觀察等價(jià)的 cpp 代碼（rust 1.71 的優(yōu)化能力并不足以將 independet 向量化，我略感悲傷）。

#include <vector>

using i32 = int;

template<typename T>
using Vec = std::vector<T>;

void dependent(Vec<i32> &a, Vec<i32> &b, Vec<i32> &c) {
    for (int i = 0; i < 9999; i++) {
        a[i] += b[i];
        b[i + 1] += c[i];
    }
    a[9999] += b[9999];
}

void independent(Vec<i32> &a, Vec<i32> &b, Vec<i32> &c) {
    a[0] += b[0];
    for (int i = 0; i < 9999; i++) {
        b[i + 1] += c[i];
        a[i + 1] += b[i + 1];
    }
}

查看匯編：

dependent(...):
    mov     rax, rdx
    mov     rdx, QWORD PTR [rsi]
    mov     rcx, QWORD PTR [rdi]
    mov     rdi, QWORD PTR [rax]
    xor     eax, eax
.L2:
    mov     esi, DWORD PTR [rdx+rax]
    add     DWORD PTR [rcx+rax], esi
    mov     esi, DWORD PTR [rdi+rax]
    add     DWORD PTR [rdx+4+rax], esi
    add     rax, 4
    cmp     rax, 39996
    jne     .L2
    mov     eax, DWORD PTR [rdx+39996]
    add     DWORD PTR [rcx+39996], eax
    ret

independent(...):
    mov     rax, QWORD PTR [rdi]
    mov     rcx, rdx
    mov     rdx, QWORD PTR [rsi]
    lea     rdi, [rax+4]
    mov     esi, DWORD PTR [rdx]
    add     DWORD PTR [rax], esi
    lea     r8, [rdx+4]
    mov     rsi, QWORD PTR [rcx]
    lea     rcx, [rdx+20]
    cmp     rdi, rcx
    lea     rdi, [rax+20]
    setnb   cl
    cmp     r8, rdi
    setnb   dil
    or      ecx, edi
    mov     rdi, rdx
    sub     rdi, rsi
    cmp     rdi, 8
    seta    dil
    test    cl, dil
    je      .L9
    mov     rcx, rax
    sub     rcx, rsi
    cmp     rcx, 8
    jbe     .L9
    mov     ecx, 4
.L7:
    movdqu  xmm0, XMMWORD PTR [rsi-4+rcx]
    movdqu  xmm2, XMMWORD PTR [rdx+rcx]
    paddd   xmm0, xmm2
    movups  XMMWORD PTR [rdx+rcx], xmm0
    movdqu  xmm3, XMMWORD PTR [rax+rcx]
    paddd   xmm0, xmm3
    movups  XMMWORD PTR [rax+rcx], xmm0
    add     rcx, 16
    cmp     rcx, 39988
    jne     .L7
    movq    xmm0, QWORD PTR [rsi+39984]
    movq    xmm1, QWORD PTR [rdx+39988]
    paddd   xmm0, xmm1
    movq    QWORD PTR [rdx+39988], xmm0
    movq    xmm1, QWORD PTR [rax+39988]
    paddd   xmm1, xmm0
    movq    QWORD PTR [rax+39988], xmm1
    mov     ecx, DWORD PTR [rdx+39996]
    add     ecx, DWORD PTR [rsi+39992]
    mov     DWORD PTR [rdx+39996], ecx
    add     DWORD PTR [rax+39996], ecx
    ret
.L9:
    mov     ecx, 4
.L6:
    mov     edi, DWORD PTR [rdx+rcx]
    add     edi, DWORD PTR [rsi-4+rcx]
    mov     DWORD PTR [rdx+rcx], edi
    add     DWORD PTR [rax+rcx], edi
    add     rcx, 4
    cmp     rcx, 40000
    jne     .L6
    retAI助手

可以看到，independent 函數(shù)被成功向量化。

責(zé)任編輯：趙寧寧來源：騰訊技術(shù)工程