作者 | 汪昊
審校 | 重樓
推薦系統(tǒng)誕生于1992 年的一篇論文。自推薦系統(tǒng)誕生以來(lái)，無(wú)數(shù)的科學(xué)家和工程師為這一領(lǐng)域傾注了心血。在過(guò)去32 年里，許多大學(xué)成立了研究推薦系統(tǒng)的研究組（比如科羅拉多大學(xué)的THAT 組），而各種各樣的公司（百度、字節(jié)跳動(dòng)等）也充分利用了推薦系統(tǒng)的獲客屬性，實(shí)現(xiàn)了低成本高收益的引流渠道。據(jù)報(bào)道，推薦系統(tǒng)能夠幫助大型網(wǎng)站實(shí)現(xiàn)30% 到40% 的流量提升。據(jù)咨詢公司Modor Intelligence 預(yù)測(cè), 2024 年推薦系統(tǒng)的世界市場(chǎng)份額會(huì)達(dá)到500 億元人民幣以上。
目前，全世界推薦引擎增長(zhǎng)最快的地區(qū)是亞太地區(qū)，而推薦系統(tǒng)的主要玩家都是大規(guī)模的云計(jì)算公司和老牌巨頭企業(yè)。在過(guò)去幾年中，沒(méi)有哪家創(chuàng)業(yè)公司能夠快速發(fā)展，吃掉大公司的市場(chǎng)份額。因此，我們可以初步認(rèn)為，推薦系統(tǒng)在全球范圍內(nèi)的發(fā)展已經(jīng)進(jìn)入了穩(wěn)定期。
2017 年以來(lái)，越來(lái)越多的專家關(guān)注到了推薦系統(tǒng)算法性能之外的問(wèn)題，特別是推薦系統(tǒng)的公平性。然而有一個(gè)非常棘手的問(wèn)題，推薦專家們一直沒(méi)能很好的解決。那就是推薦系統(tǒng)的冷啟動(dòng)問(wèn)題。在沒(méi)有數(shù)據(jù)的情況下，我們?cè)撛趺唇鉀Q推薦的難題？為了介紹相關(guān)知識(shí)，我們先介紹一下零樣本學(xué)習(xí)的發(fā)展歷程。零樣本學(xué)習(xí)發(fā)端自21 世紀(jì)的頭十年，然而過(guò)去20 年的零樣本算法，基本都需要遷移學(xué)習(xí)或者元學(xué)習(xí)，沒(méi)有一個(gè)算法能成為真正的零樣本學(xué)習(xí)。這一狀況一直等到了2021 年ZeroMat 被發(fā)明出來(lái)后才得以改變（ZeroMat 的源代碼地址：https://github.com/haow85/ZeroMat），后續(xù)陸陸續(xù)續(xù)有新的零樣本算法出現(xiàn)，讓人們意識(shí)到即便不使用任何數(shù)據(jù)，我們也可以把推薦做的很好。
2023 年 Ratidar Technologies LLC 公司 （公司官網(wǎng)：http://ratidar.mysxl.cn）推出了一款不需要數(shù)據(jù)的推薦系統(tǒng)算法 LogitMat（論文下載地址：https://arxiv.org/ftp/arxiv/papers/2307/2307.05680.pdf）。該算法利用了邏輯回歸和矩陣分解結(jié)合的方式，在不使用輸入數(shù)據(jù)的情況下，完美地完成了推薦的任務(wù)。下面我們來(lái)看一下這個(gè)算法的細(xì)節(jié)：
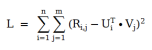
上面這個(gè)公式是矩陣分解的損失函數(shù)。簡(jiǎn)單來(lái)說(shuō)，就是我們需要計(jì)算出用戶特征向量 U 和物品特征向量V, 以便使得他們的點(diǎn)乘和用戶評(píng)分的差值最小。可以看出來(lái)，矩陣分解算法本質(zhì)上是一個(gè)降維算法。我們利用向量點(diǎn)乘將用戶評(píng)分矩陣的O(mn) 空間復(fù)雜度降為 O(k(m+n))，其中m 是用戶數(shù)、n 是物品數(shù)、k 是向量長(zhǎng)度。通常k 遠(yuǎn)小于m 或 n ，因此矩陣分解算法有效的降低了算法的空間復(fù)雜度。
我們發(fā)現(xiàn)電影評(píng)分服從冪律分布，因此我們可以用評(píng)分值本身來(lái)替換評(píng)分的分布。如果我們用邏輯回歸來(lái)表示評(píng)分的分布，也就等價(jià)于用邏輯回歸來(lái)計(jì)算評(píng)分值。我們得到下面的公式：
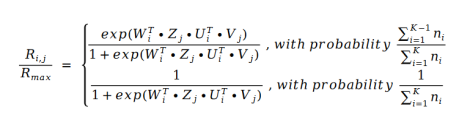
其中 U 和 V 就是矩陣分解中的 U 和 V，而 W 和Z 是系數(shù)。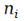
的值就是下標(biāo)I 本身。那么我們把這個(gè)公式帶入到矩陣分解的損失函數(shù)公式中去，得到下面的損失函數(shù)公式：
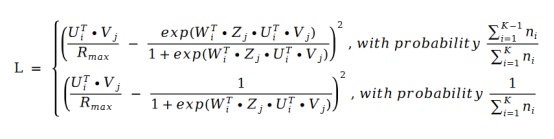
利用隨機(jī)梯度下降對(duì)該損失函數(shù)求導(dǎo)。我們得到了如下的公式：
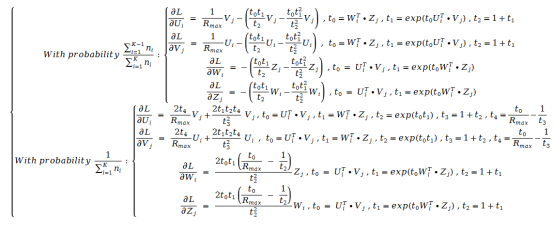
雖然公式看起來(lái)非常復(fù)雜，但其實(shí)實(shí)現(xiàn)起來(lái)只需要比對(duì)公式正常輸入就可以，因此實(shí)現(xiàn)難度并不大。
LogitMat 的發(fā)明人隨后在MovieLens 1 Million Dataset 和 LDOS-CoMoDa Dataset 兩個(gè)不同的數(shù)據(jù)集合上驗(yàn)證了該算法的準(zhǔn)確率和公平性。MovieLens 1 Million Dataset 由6040 名用戶和3952 部電影的評(píng)分組成，而LDOS-CoMoDa Dataset 是個(gè)更小的數(shù)據(jù)集合。作者在測(cè)評(píng)準(zhǔn)確率的時(shí)候使用了MAE 指標(biāo)。之所以作者使用 MAE 指標(biāo)，是因?yàn)樵撝笜?biāo)歷史最為悠久，能夠和海量論文實(shí)驗(yàn)數(shù)據(jù)作對(duì)比。而在測(cè)評(píng)公評(píng)性的時(shí)候，作者采用了 Degree of Matthew Effect。
實(shí)驗(yàn)結(jié)果如下：
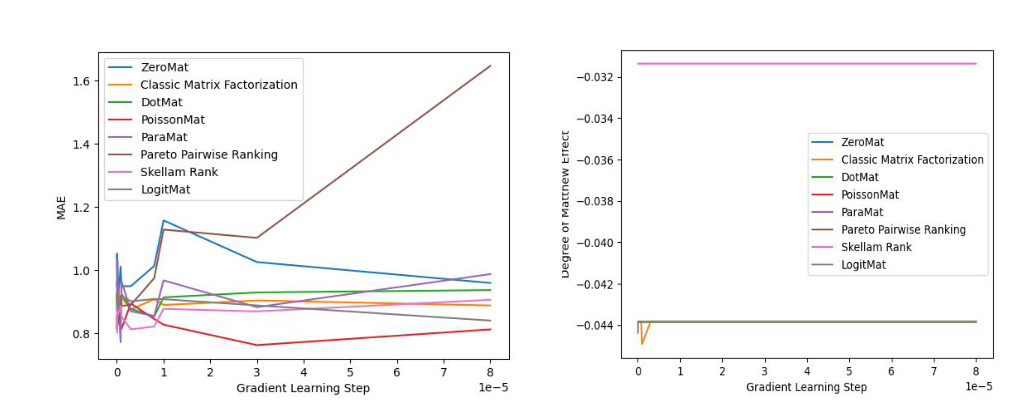
上圖顯示了LogitMat 和4 種零樣本學(xué)習(xí)，2 種排序?qū)W習(xí)和經(jīng)典的矩陣分解算法的對(duì)比效果，LogitMat 取得了第2 名的好成績(jī)。
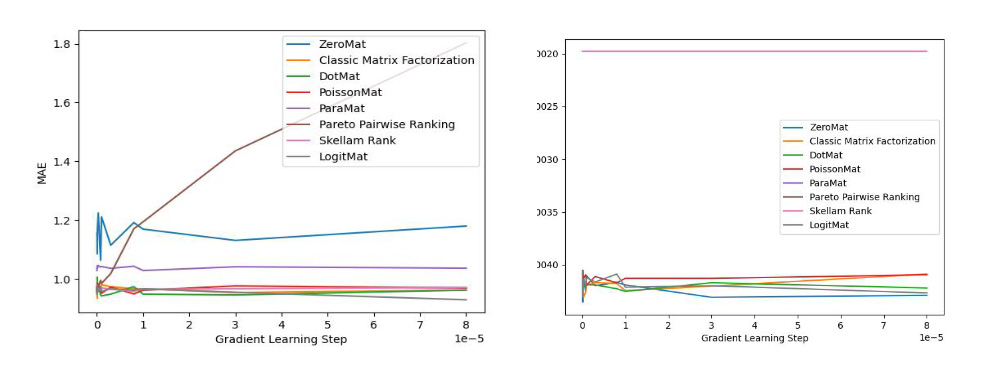
上圖顯示了算法在 LDOS-CoMoDal 數(shù)據(jù)集合上的測(cè)評(píng)結(jié)果。同樣的，LogitMat 算法的效果非常理想，讓人拍案叫絕。
LogitMat 是不需要數(shù)據(jù)的推薦系統(tǒng)算法，因?yàn)樵谒惴ǖ那蠼膺^(guò)程中沒(méi)有出現(xiàn)評(píng)分矩陣的評(píng)分值 R。利用這個(gè)思路，我們可以設(shè)計(jì)出許多新的零樣本學(xué)習(xí)算法。這一切聽(tīng)上去似乎非常可怕——我們可以不利用任何數(shù)據(jù)預(yù)測(cè)我們喜歡什么電影。而這并不需要花多少的計(jì)算資源就可以實(shí)現(xiàn)。事實(shí)上，我只要有一臺(tái) 2024 年的手提電腦就可以預(yù)測(cè)成千上萬(wàn)人的興趣愛(ài)好。
需要注意的是，我們只需要修改 W 和 Z ，把他們改成更為復(fù)雜的形式，就可以把 LogitMat 變?yōu)樯疃葘W(xué)習(xí)模型。基于深度學(xué)習(xí)的零樣本學(xué)習(xí)算法，其實(shí)離我們也并不太遙遠(yuǎn)了。也許有一天，我們會(huì)發(fā)現(xiàn)，所謂的推薦系統(tǒng)和評(píng)分體系不過(guò)是一場(chǎng)人類歷史上的美麗誤會(huì)。僅僅因?yàn)槲覀兣艿奶欤覀兺俗约旱臄?shù)學(xué)根基并不牢靠。或許，推薦系統(tǒng)有著我們長(zhǎng)久忽略的社會(huì)學(xué)意義，就像下面這篇論文中描述的：Human Culture: A History Irrelevant and Predictable Experience （論文下載地址：https://arxiv.org/ftp/arxiv/papers/2307/2307.13882.pdf），人類的文化因?yàn)閮缏涩F(xiàn)象和時(shí)間無(wú)關(guān)現(xiàn)象被鎖死了。
作者簡(jiǎn)介
汪昊，前 Funplus 人工智能實(shí)驗(yàn)室負(fù)責(zé)人。曾在 ThoughtWorks、豆瓣、百度、新浪等公司擔(dān)任技術(shù)和技術(shù)高管職務(wù)。在互聯(lián)網(wǎng)公司和金融科技、游戲等公司任職 13 年，對(duì)于人工智能、計(jì)算機(jī)圖形學(xué)和區(qū)塊鏈等領(lǐng)域有著深刻的見(jiàn)解和豐富的經(jīng)驗(yàn)。在國(guó)際學(xué)術(shù)會(huì)議和期刊發(fā)表論文 42 篇，獲得IEEE SMI 2008 最佳論文獎(jiǎng)、ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023 / ICSIM 2024最佳論文報(bào)告獎(jiǎng)。
