本文經(jīng)自動(dòng)駕駛之心公眾號(hào)授權(quán)轉(zhuǎn)載，轉(zhuǎn)載請(qǐng)聯(lián)系出處。

寫在前面&筆者的個(gè)人理解

實(shí)時(shí)根據(jù)傳感器數(shù)據(jù)構(gòu)建向量化高精地圖對(duì)于預(yù)測(cè)和規(guī)劃等下游任務(wù)至關(guān)重要，可以有效彌補(bǔ)離線高精地圖實(shí)時(shí)性差的缺點(diǎn)。隨著深度學(xué)習(xí)的發(fā)展，在線向量化高精地圖構(gòu)建逐漸興起，代表性的工作如HDMapNet，MapTR等相繼涌現(xiàn)。然而，現(xiàn)有的在線向量化高精地圖構(gòu)建方法缺乏對(duì)地圖元素幾何性質(zhì)（包括元素的形狀，垂直、平行等幾何關(guān)系）的探索。

向量化高精地圖的幾何性質(zhì)

向量化高精地圖對(duì)道路上的元素進(jìn)行了高度抽象，將每一個(gè)地圖元素表示為二維點(diǎn)序列。而城市道路的設(shè)計(jì)具有特定的規(guī)范，例如，人行橫道在多數(shù)情況下表現(xiàn)為方正的矩形或平行四邊形；在不涉及分流合流的路段,相鄰的兩條車道互相平行。高精地圖中不同元素還具有許多類似的特點(diǎn)，這些常識(shí)性的規(guī)律，抽象為高精地圖的幾何性質(zhì)，包括地圖元素的形狀（矩形、平行四邊形、直線等），或者不同地圖元素之間的關(guān)聯(lián)（平行、垂直等）。幾何性質(zhì)強(qiáng)有力地約束著地圖元素的表現(xiàn)形式，在線構(gòu)建模型如果充分理解了幾何性質(zhì)，就能得到更精確的結(jié)果。

提出針對(duì)高精地圖的幾何表示的重要性

盡管理論上現(xiàn)有模型仍可能學(xué)到地圖元素的幾何性質(zhì)，然而，幾何性質(zhì)的特點(diǎn)決定了至少在傳統(tǒng)的設(shè)計(jì)下，模型并不容易學(xué)到。

• 幾何性質(zhì)的不變性

中心車輛在道路上直線行駛，變道，或者轉(zhuǎn)彎時(shí)，（在車輛坐標(biāo)系下）地圖元素的絕對(duì)坐標(biāo)不斷發(fā)生變化。而人行橫道、車道、道路邊界等的形狀并不會(huì)隨之改變；類似的，車道之間平行關(guān)系也不會(huì)改變。地圖元素的幾何性質(zhì)是客觀的，它的一個(gè)重要特點(diǎn)就是不變性。更具體的，是剛性不變性（對(duì)旋轉(zhuǎn)、平移變換保持不變）。以往的工作，不論是使用樸素的折線表示，還是使用帶控制點(diǎn)的多項(xiàng)式曲線（比如貝塞爾曲線、分段貝塞爾曲線），都基于絕對(duì)坐標(biāo)，并在絕對(duì)坐標(biāo)基礎(chǔ)上端到端優(yōu)化。基于絕對(duì)坐標(biāo)的優(yōu)化目標(biāo)本身不具備剛性不變性，因此很難期待模型陷入的局部最優(yōu)解包含對(duì)幾何性質(zhì)的理解。因此，一種能充分刻畫幾何性質(zhì)且具有一定不變性的表示是必要的。

圖1. 幾何不變性的示例。

車輛右轉(zhuǎn)時(shí)，絕對(duì)坐標(biāo)會(huì)發(fā)生明顯的變化。右圖展示了一個(gè)對(duì)應(yīng)的真實(shí)場(chǎng)景。

• 幾何性質(zhì)的多樣性

此外，盡管具有強(qiáng)烈的先驗(yàn)知識(shí)，道路的幾何性質(zhì)仍然是多樣的。這些多樣的幾何性質(zhì)總體上可以分為兩大類，一類是關(guān)于單個(gè)地圖元素的幾何形狀，一類是關(guān)于不同地圖元素的幾何關(guān)聯(lián)。由于幾何性質(zhì)的多樣性，窮舉并人工地將幾何性質(zhì)轉(zhuǎn)變?yōu)榧s束是不可能的，因此我們更希望模型能夠端到端地自主學(xué)習(xí)多樣的幾何性質(zhì)。

GeMap的設(shè)計(jì)

幾何表示

針對(duì)上述兩個(gè)問題，我們首先改進(jìn)表示方法。我們希望在傳統(tǒng)的基于絕對(duì)坐標(biāo)的表示之外，引入一種良好的幾何表示，它需要滿足：

• 能刻畫地圖元素的形狀
• 能刻畫地圖元素之間的關(guān)聯(lián)
• 剛性不變性

為保證平移不變性，我們使用了相對(duì)量，即點(diǎn)之間的偏移向量；為進(jìn)一步保證旋轉(zhuǎn)不變性，我們選擇了偏移向量的長(zhǎng)度，以及不同偏移向量之間的夾角。這二者——長(zhǎng)度和夾角——構(gòu)成了我們提出的幾何表示的基礎(chǔ)。此外，為了更好地區(qū)分并刻畫形狀、關(guān)聯(lián)兩類不同的幾何性質(zhì)，我們還按照從簡(jiǎn)的原則進(jìn)一步細(xì)化了設(shè)計(jì)：

為刻畫形狀，我們計(jì)算單個(gè)地圖元素中相鄰點(diǎn)之間的偏移向量，并計(jì)算偏移向量長(zhǎng)度、相鄰偏移向量之間的夾角。這一表示能夠唯一確定任意的折線/多邊形。兩個(gè)形象的例子如下圖所示：

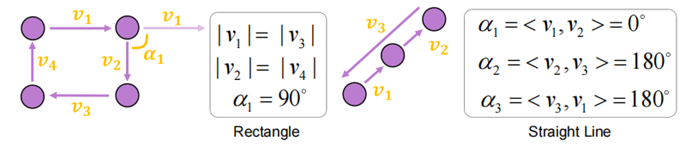
圖2. 幾何形狀表示。

對(duì)于一個(gè)矩形，使用一個(gè)直角和兩對(duì)相等的邊就可以描述；對(duì)于一條直線，所有的夾角均為0度或者180。

為刻畫關(guān)聯(lián)，類似地，我們首先考慮了任意兩點(diǎn)之間的距離。然而，如果對(duì)所有點(diǎn)對(duì)點(diǎn)的偏移向量?jī)蓛捎?jì)算夾角，表示的復(fù)雜度過高，且計(jì)算代價(jià)不可承受。具體地，假設(shè)一共有個(gè)地圖元素，每個(gè)元素使用個(gè)個(gè)點(diǎn)來表示，那么所有夾角的數(shù)據(jù)量將達(dá)到（取1000時(shí)，假設(shè)每一個(gè)角度數(shù)據(jù)都是32位浮點(diǎn)數(shù)，這樣的表示僅占據(jù)的空間將達(dá)到TB級(jí)別）。事實(shí)上，對(duì)于一般的垂直、平行等關(guān)系來說這不是必要的。因此，我們先計(jì)算元素內(nèi)部的偏移，然后僅對(duì)這些偏移計(jì)算兩兩之間的夾角作為幾何表示的一部分。這種簡(jiǎn)化的關(guān)聯(lián)表示保留了對(duì)平行、垂直等關(guān)系的描述能力，同時(shí)所對(duì)應(yīng)的數(shù)據(jù)量?jī)H為（前述條件下，大致4MB）。為了便于理解，我們同樣提供了一些例子：

圖3. 幾何關(guān)聯(lián)表示。

平行關(guān)系和垂直關(guān)系表現(xiàn)為偏移向量的夾角為0度或者90度；兩點(diǎn)之間的距離可以一定程度反映車道寬度信息

為優(yōu)化幾何形狀和關(guān)聯(lián)的表示，我們采用最樸素的做法，直接計(jì)算預(yù)測(cè)和標(biāo)簽的幾何表示，然后用范數(shù)作為優(yōu)化目標(biāo)：

這里和分別表示根據(jù)標(biāo)簽計(jì)算得到的長(zhǎng)度和夾角，和則表示根據(jù)預(yù)測(cè)計(jì)算得到的長(zhǎng)度和夾角。在處理夾角時(shí)使用了一個(gè)技巧：直接計(jì)算角度涉及到不連續(xù)的arctan函數(shù)，在優(yōu)化時(shí)會(huì)遇到困難（在±90度附近存在梯度消失的問題），因此我們實(shí)際上比較的是夾角的余弦和正弦值：

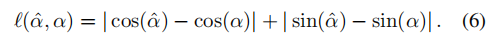
幾何表示的基礎(chǔ)是角度和距離，因此我們形象地將對(duì)應(yīng)的幾何損失稱為”歐幾里得損失“，也代表著這一損失對(duì)于旋轉(zhuǎn)和平移變換的魯棒性。

幾何解耦注意力

一種被MapTR，PivotNet等采用的架構(gòu)將地圖元素上的每一個(gè)點(diǎn)對(duì)應(yīng)到Transformer的一個(gè)查詢。這一架構(gòu)的問題在于：對(duì)兩大類的幾何性質(zhì)不加區(qū)分。

在自注意力中，所有查詢（也就是“點(diǎn)”）之間都平等地相互作用。然而，地圖元素的形狀對(duì)應(yīng)著一組一組的查詢。這些組之間的交互，在感知元素形狀時(shí)就成為了累贅。反之在感知元素之間關(guān)聯(lián)的時(shí)候，形狀亦成為了冗余因素。這意味著將形狀、關(guān)聯(lián)的感知解耦，可能帶來更好的結(jié)果。

為了解耦對(duì)幾何形狀和關(guān)聯(lián)處理，我們將自注意力分成兩個(gè)步驟進(jìn)行：

• 每個(gè)地圖元素包括個(gè)查詢，在這個(gè)查詢內(nèi)部進(jìn)行注意力，用以處理幾何形狀
• 補(bǔ)充跨元素的注意力關(guān)系，用以處理幾何關(guān)聯(lián)

幾何解耦的注意力更形象的表示如下圖所示。我們的實(shí)現(xiàn)方式比較樸素，直接使用mask控制注意力的范圍。事實(shí)上，由于這兩種注意力是互補(bǔ)的，合理地實(shí)現(xiàn)有可能讓時(shí)間復(fù)雜度等同于進(jìn)行單次自注意力。

圖4. 幾何解耦注意力。

左側(cè)為單個(gè)元素內(nèi)部進(jìn)行的形狀注意力，右側(cè)為元素之間進(jìn)行的關(guān)聯(lián)注意力。

實(shí)驗(yàn)結(jié)果

我們?cè)趎uScenes和Argoverse 2兩個(gè)數(shù)據(jù)集上進(jìn)行了大量實(shí)驗(yàn)。二者都是常用的大規(guī)模自動(dòng)駕駛數(shù)據(jù)集，且都提供了地圖標(biāo)注。

主要結(jié)果

在nuScenes上，我們進(jìn)行了三組實(shí)驗(yàn)。我們首先使用了一種比較純粹的目標(biāo)函數(shù)組合，只包括幾何損失和其它必要的損失（如點(diǎn)到點(diǎn)距離、邊的方向、分類），這一組合是為了體現(xiàn)我們提出的幾何性質(zhì)的重要價(jià)值，而不過多追求SOTA的結(jié)果。可以看到，在這種情況下，相比于MapTR，我們的方法能在mAP提升了。為了探索GeMap的極限，我們也加上了一些輔助目標(biāo)，包括分割和深度估計(jì)，在這種情況下我們也取得了SOTA的結(jié)果（mAP提升）。值得注意的是，取得這樣的提升并不需要犧牲太多的推理速度。最后，我們還嘗試了引入額外的LiDAR模態(tài)輸入，在額外模態(tài)輸入的加持下，GeMap的性能也能取得進(jìn)一步提升。

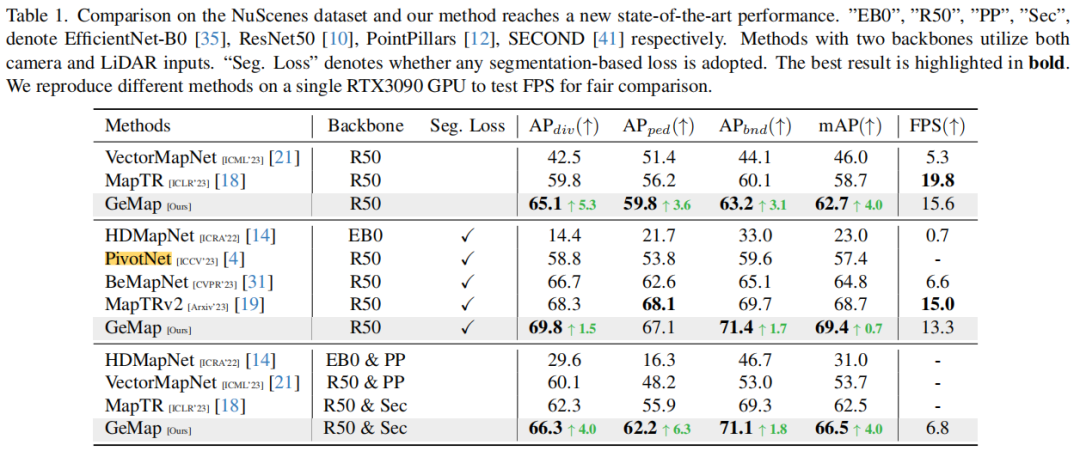
同樣，在Argoverse 2數(shù)據(jù)集上，我們的方法也取得了非常突出的效果。

消融實(shí)驗(yàn)

在nuScenes上進(jìn)一步進(jìn)行的消融實(shí)驗(yàn)證明了幾何損失和幾何解耦注意力的價(jià)值。有趣的是，正如我們所預(yù)料的，直接使用幾何損失反而會(huì)帶來模型表現(xiàn)的下降。我們認(rèn)為這是因?yàn)?strong>結(jié)構(gòu)上的對(duì)形狀和關(guān)聯(lián)處理的耦合，導(dǎo)致模型很難優(yōu)化幾何表示；而在與幾何解耦注意力結(jié)合之后，幾何損失就發(fā)揮了應(yīng)有的作用（從”+Euclidean Loss“到”Full“）。

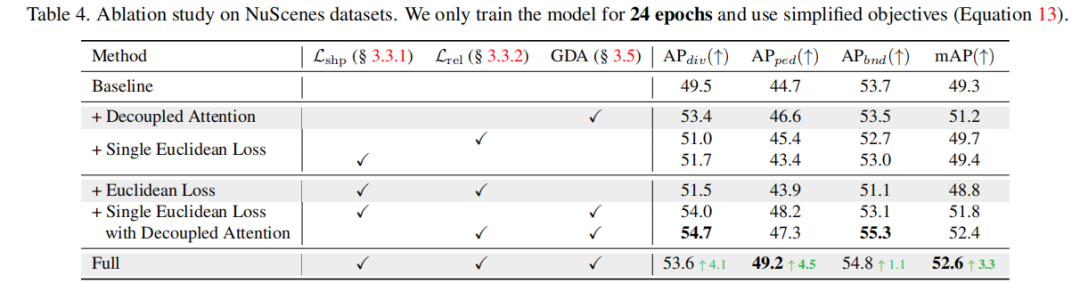
更多結(jié)果

此外，我們還在nuScenes上進(jìn)行了可視化分析。可視化的結(jié)果表明，GeMap除了具有對(duì)旋轉(zhuǎn)和平移的魯棒性，在處理遮擋問題上也表現(xiàn)出了一定優(yōu)勢(shì)，如下圖。圖中有挑戰(zhàn)性的地圖元素使用橘色方框標(biāo)出。

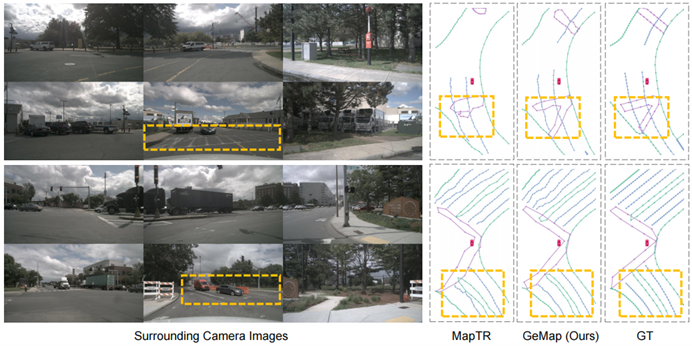
圖5. 可視化對(duì)比結(jié)果。

關(guān)于對(duì)遮擋的魯棒性，在雨天的實(shí)驗(yàn)結(jié)果中（見下表”“）也得到了定量驗(yàn)證（因?yàn)橛晁畬?duì)相機(jī)有天然的遮擋）：

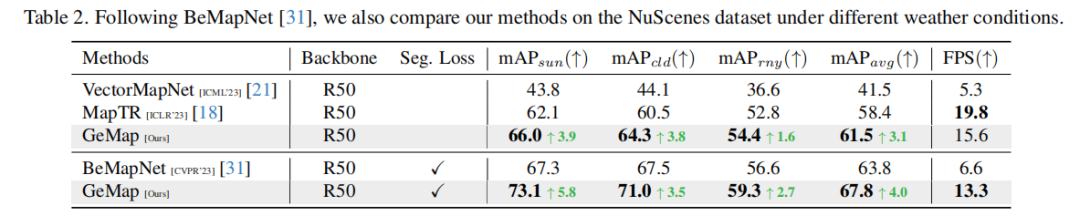
這可以解釋為模型學(xué)到了幾何性質(zhì)，因此即使有遮擋，也能更好地猜出地圖元素。例如，模型理解了車道線的形狀，那么只需要”看到“一部分，就能夠估計(jì)剩下的部分；模型理解了車道線之間的平行關(guān)系，或者車道的寬度特點(diǎn)，因此哪怕其中一條被遮擋，也能根據(jù)平行、寬度因素猜測(cè)被遮擋的部分。

總結(jié)

我們指出了地圖元素所具有的幾何性質(zhì)，以及其對(duì)于在線向量化高精地圖構(gòu)建的價(jià)值。基于此，我們提出了一種強(qiáng)有力的方法，初步對(duì)這一價(jià)值進(jìn)行了驗(yàn)證。此外，GeMap表現(xiàn)出的對(duì)遮擋的魯棒性，或許預(yù)示著在其它自動(dòng)駕駛?cè)蝿?wù)（例如檢測(cè)、占有預(yù)測(cè)等）中利用幾何性質(zhì)處理遮擋的思路——因?yàn)檐囕v和道路都具有相對(duì)規(guī)范的幾何性質(zhì)。當(dāng)然，我們的方法本身也有很多可以進(jìn)一步探索的地方。比如不同復(fù)雜度的幾何元素是否可以適應(yīng)性地使用不同的點(diǎn)來描述？是否能從概率的角度出發(fā)理解幾何表示，讓其對(duì)噪音更具魯棒性？因?yàn)槲覀儗?duì)于元素關(guān)聯(lián)進(jìn)行了簡(jiǎn)化，那么是否存在更好的幾何關(guān)聯(lián)的表示方法？這些都是進(jìn)一步優(yōu)化的方向。

原文鏈接：https://mp.weixin.qq.com/s/BoxlskT68Kjb07mfwQ7Swg