程序員必須掌握這幾種排序算法的優秀實踐,包會!(含GIF圖)

排序是計算機中常見且重要的操作,用于使數據按照某種規則或標準進行有序化,便于后續的搜索、查找和處理。
為什么排序算法很重要?
由于排序通常有助于降低問題的算法復雜性,因此它在計算機科學中具有重要用途。百度搜索顯示,當今計算世界中有 40 多種不同的排序算法。瘋狂吧?那你知道幾個呢!
現實世界中實現這一點的一些最佳示例是。
- 冒泡排序用于電視節目中,根據觀眾觀看時間對頻道進行排序!
- 數據庫使用外部合并排序對太大而無法完全加載到內存中的數據集進行排序!
- 體育比分通過快速排序算法實時快速組織!
數據結構中的排序類型
- 基于比較的排序:在基于比較的排序技術中,定義比較器來比較數據樣本的元素或項目。該比較器定義元素的順序。例子有:冒泡排序、歸并排序。
- 基于計數的排序:這些類型的排序算法中的元素之間不涉及比較,而是在執行過程中進行計算假設。例如:計數排序、基數排序。
- 就地與非就地排序(In-Place vs Not-in-Place Sorting):數據結構中的就地排序技術會修改原始數組中數組元素的順序。另一方面,非就地排序技術使用輔助數據結構對原始數組進行排序。就地排序技術的示例有:冒泡排序、選擇排序。非就地排序算法的一些示例包括:合并排序、快速排序。
PS:GIF圖較大,耐心等待打開,值得反復去看!
1、冒泡排序
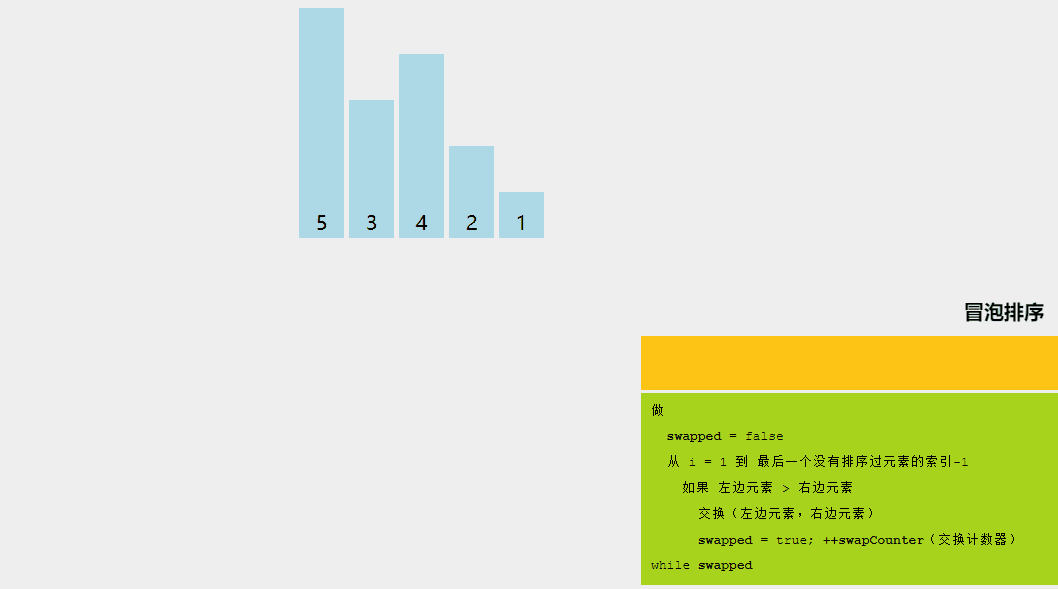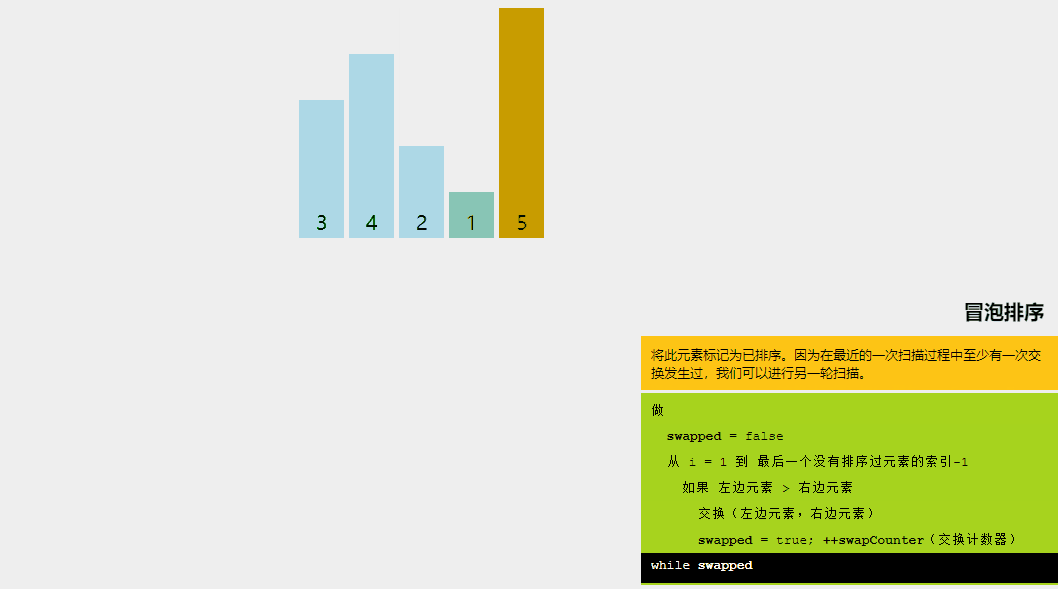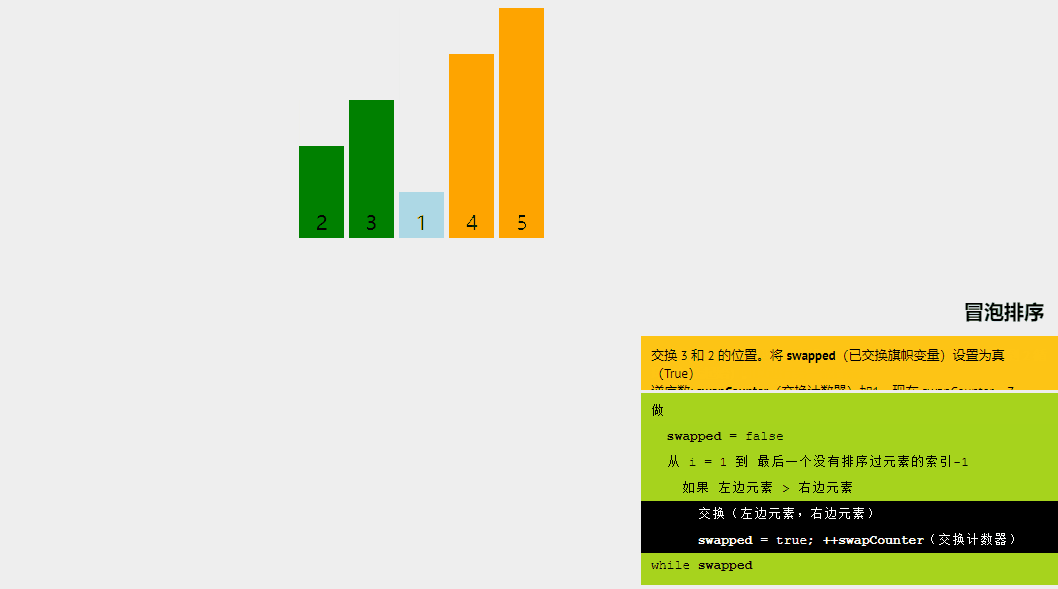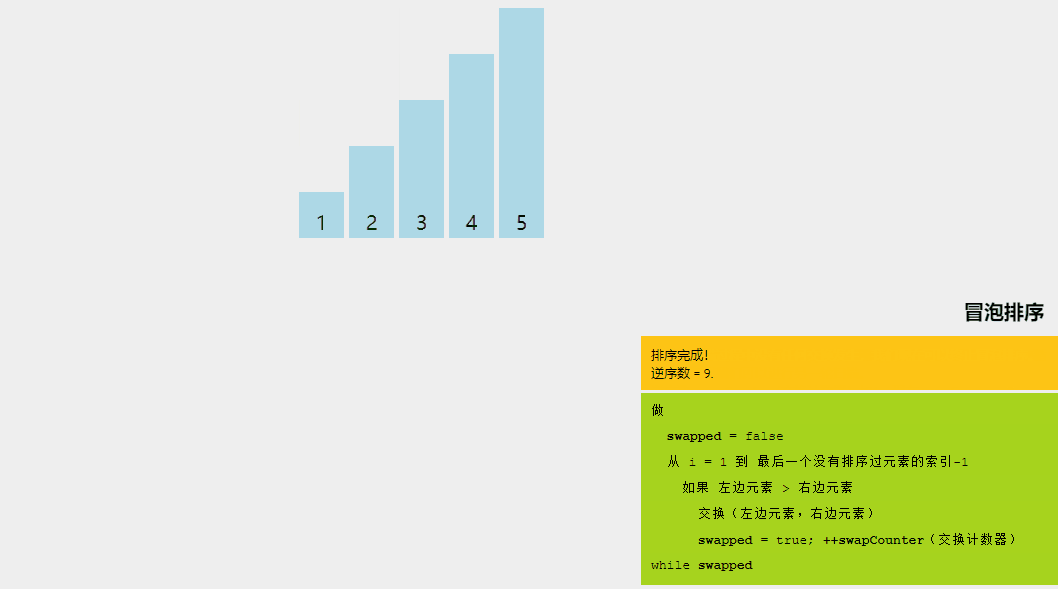
冒泡排序的基本思想是,如果相鄰元素的順序不符合要求,則重復交換相鄰元素。是的,就是這么簡單。
如果給定的數組元素必須按升序排序,則冒泡排序將首先比較數組的第一個元素與第二個元素,如果結果大于第二個元素,則立即交換它們,然后繼續比較第二個和第三個元素,依此類推。
讓我們嘗試通過一個例子來理解冒泡排序背后的直觀方法:

冒泡排序算法解釋
Java 中的實現
import java.util.Arrays;
public class BubbleSort {
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
public static void main(String[] args) {
int[] arr = {5, 3, 4, 2, 1};
bubbleSort(arr);
System.out.println("Sorted array: ");
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
}冒泡排序的實現
時間復雜度:
- 最壞情況: O(n^2)
- 平均情況:O(n*logn)
- 最好的情況:O(n*logn)
空間復雜度: O(1)。
2、選擇排序
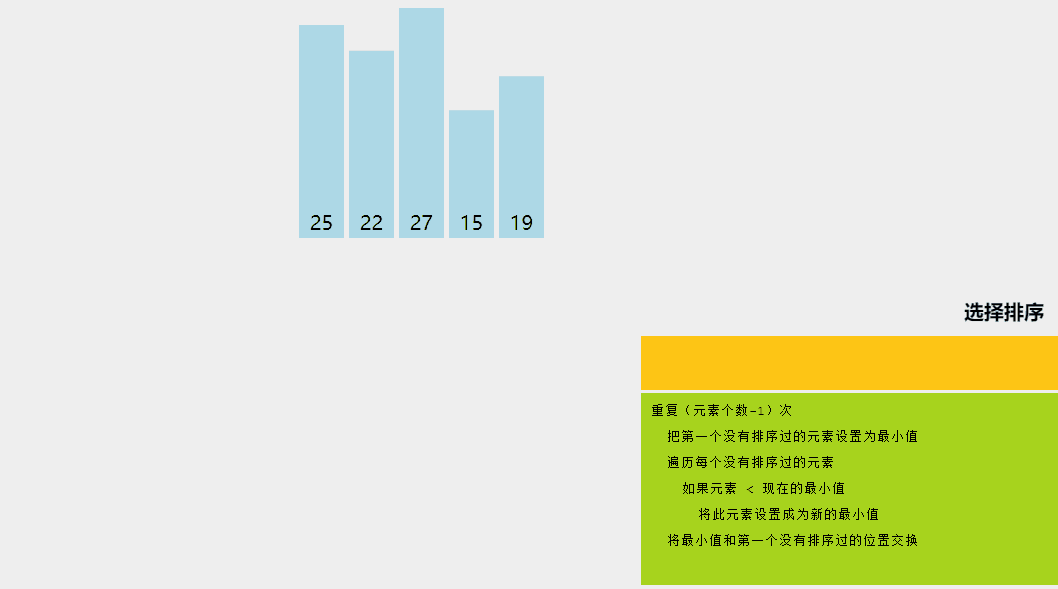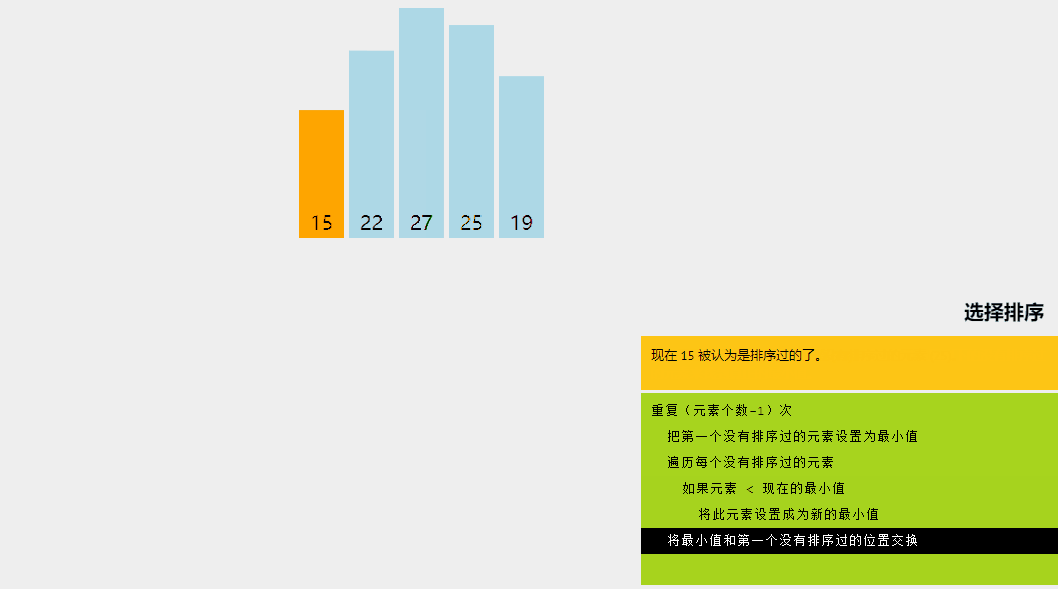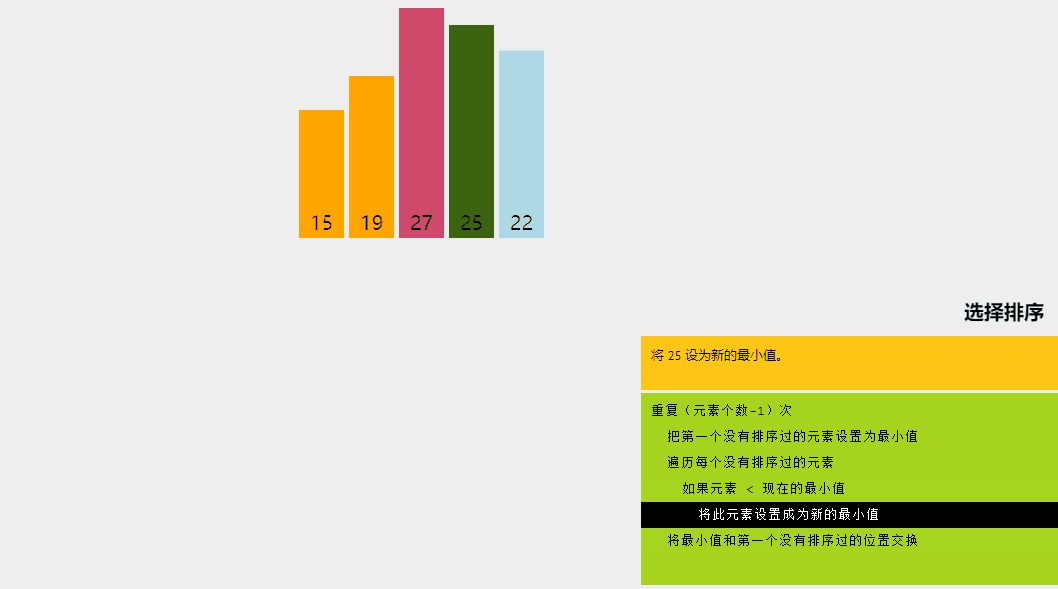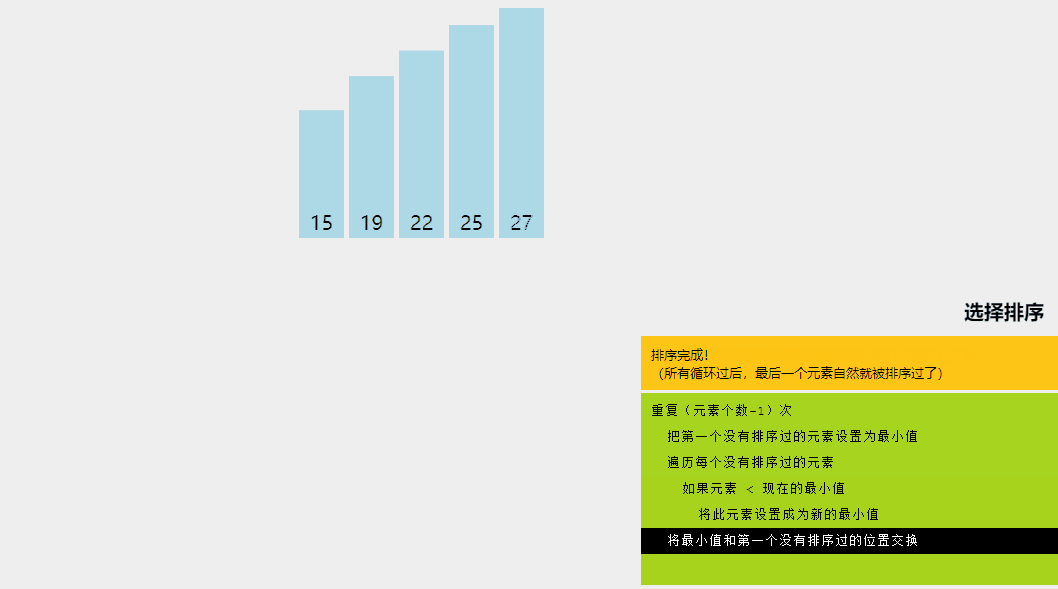
選擇排序是一種排序算法,其中給定數組分為兩個子數組:已排序的左部分和未排序的右部分。
最初,已排序部分為空,未排序部分是整個列表。在每次迭代中,我們從未排序列表中獲取最小元素并將其推送到已排序列表的末尾,從而構建已排序的數組。
讓我們嘗試用一個簡單的例子來理解選擇排序背后的直觀想法:

選擇排序算法解釋
Java 中的實現
import java.util.Arrays;
public class SelectionSort {
public static void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
public static void main(String[] args) {
int[] arr = {25, 22, 27, 15, 19};
selectionSort(arr);
System.out.println("Sorted array:");
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
}選擇排序的實現
時間復雜度:
- 最壞情況: O(n*n)
- 平均情況: O(n*logn)
- 最好情況: O(n*logn)
空間復雜度: O(1)。
3、插入排序

插入排序是一種將給定數組分為已排序部分和未排序部分的排序算法。在每次迭代中,要插入的元素必須在已排序的子序列中找到其最佳位置,然后插入,同時將剩余元素向右移動。
通過示例了解插入排序算法。
下面是一個例子,可以幫助更好地理解插入排序:

插入排序算法解釋
現在已經了解了插入排序的實際工作原理,接下來看一下 Java的 實現。
import java.util.Arrays;
public class InsertionSort {
public static void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
public static void main(String[] args) {
int[] arr = {25, 22, 27, 15, 19};
insertionSort(arr);
System.out.println(Arrays.toString(arr));
}
}插入排序的實現
時間復雜度:
- 最壞情況: O(n*n)
- 平均情況: O(n*logn)
- 最好情況: O(n*logn)
空間復雜度: O(1)。
4、快速排序
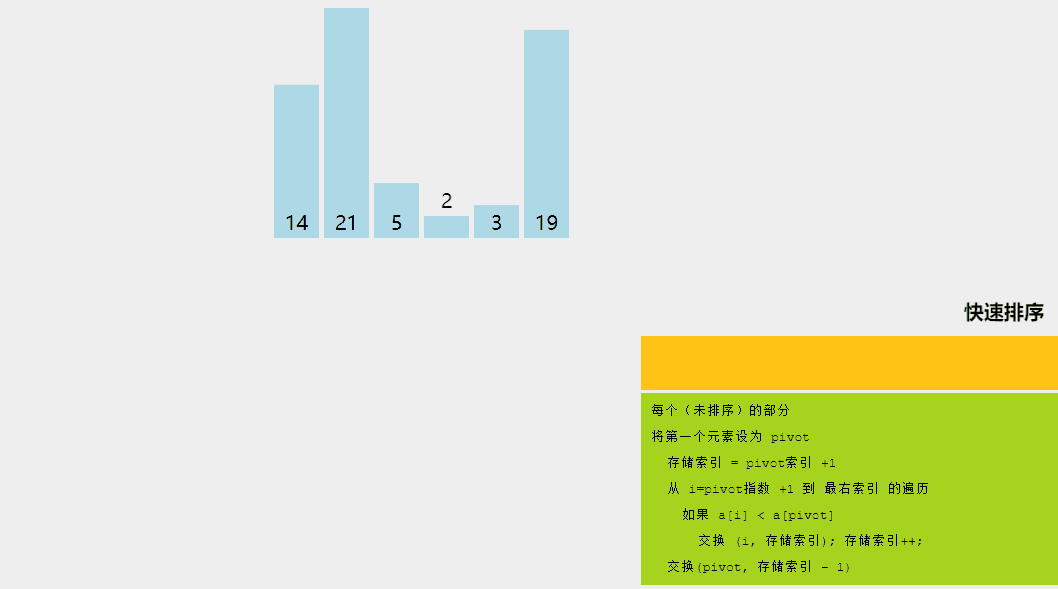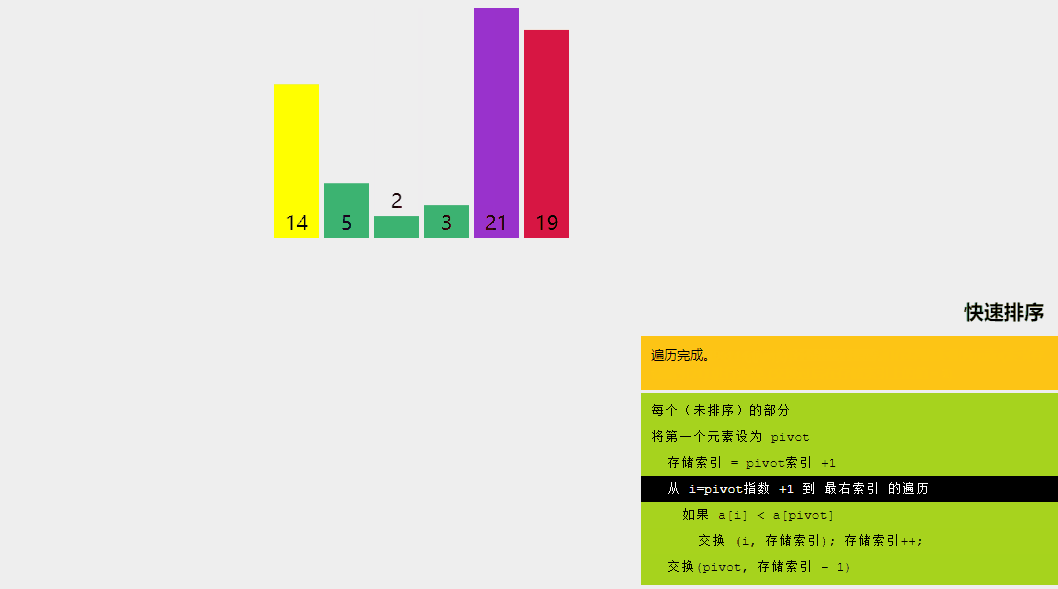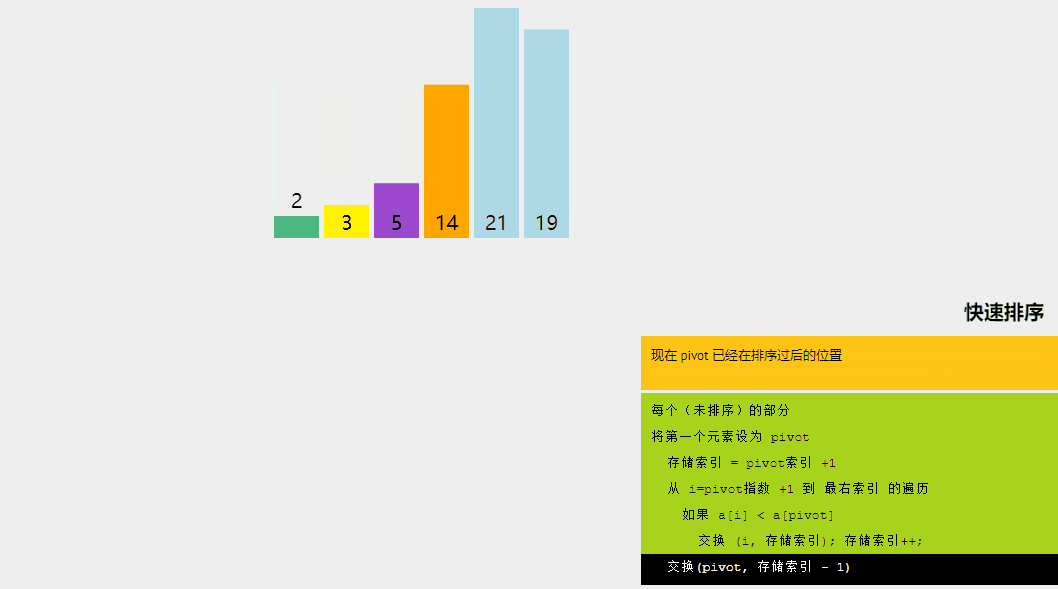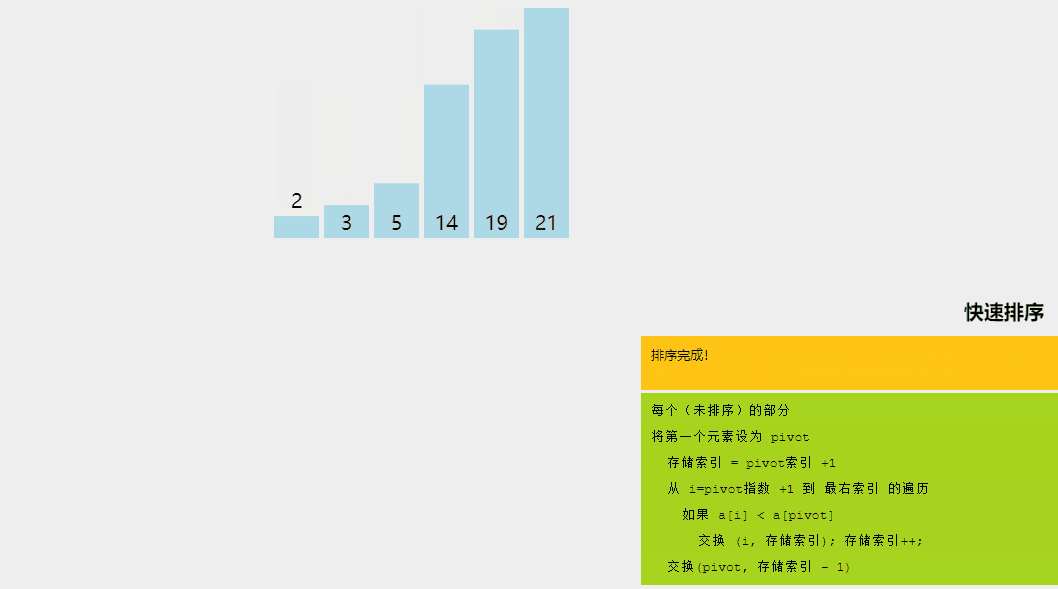
快速排序是一種分而治之的算法。快速排序背后的直觀概念是,它從給定的元素數組中選擇一個元素作為主元,然后圍繞主元元素對數組進行分區。隨后,它遞歸地調用自身并隨后對兩個子數組進行分區。
通過可視化了解快速排序算法。
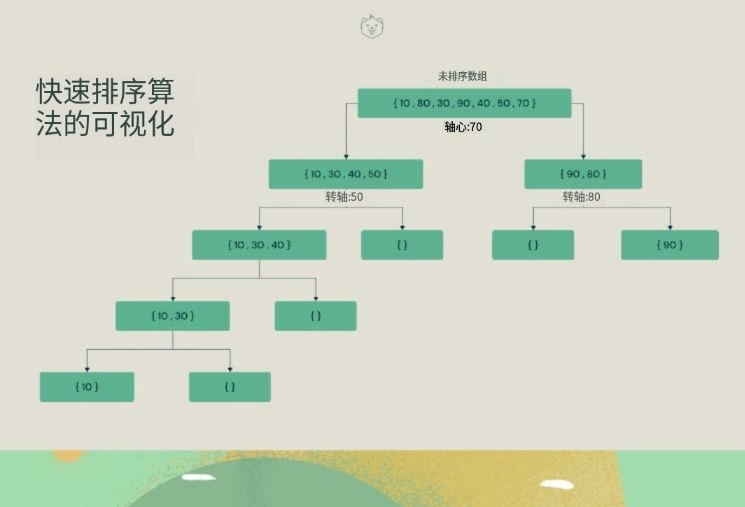
快速排序算法涉及的邏輯步驟如下:
- 樞軸選擇:選擇一個元素作為樞軸(這里,我們選擇最后一個元素作為樞軸)。
- 分區:數組的分區方式使得所有小于主元的元素都位于左子數組中,而所有嚴格大于主元的元素都存儲在右子數組中。
- 遞歸調用快速排序:對上面創建的兩個子數組再次調用快速排序函數,并重復步驟。
下面的實現中包含了注釋,以幫助更好地理解快速排序算法。
import java.util.Arrays;
public class QuickSort {
public static int partition(int[] arr, int low, int high) {
int pivot = arr[high];
int i = low - 1;
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return i + 1;
}
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int partitionIndex = partition(arr, low, high);
quickSort(arr, low, partitionIndex - 1);
quickSort(arr, partitionIndex + 1, high);
}
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] arr = {14, 21, 5, 2, 3, 19};
int n = arr.length;
quickSort(arr, 0, n - 1);
System.out.print("Sorted array: ");
for (int i = 0; i < n; i++) {
System.out.print(arr[i] + " ");
}
}
}快速排序的實現
時間復雜度:
- 最壞情況: O(n*n)
- 平均情況: O(n*logn)
- 最好情況: O(n*logn)
空間復雜度: O(1)。
5、隨機快速排序
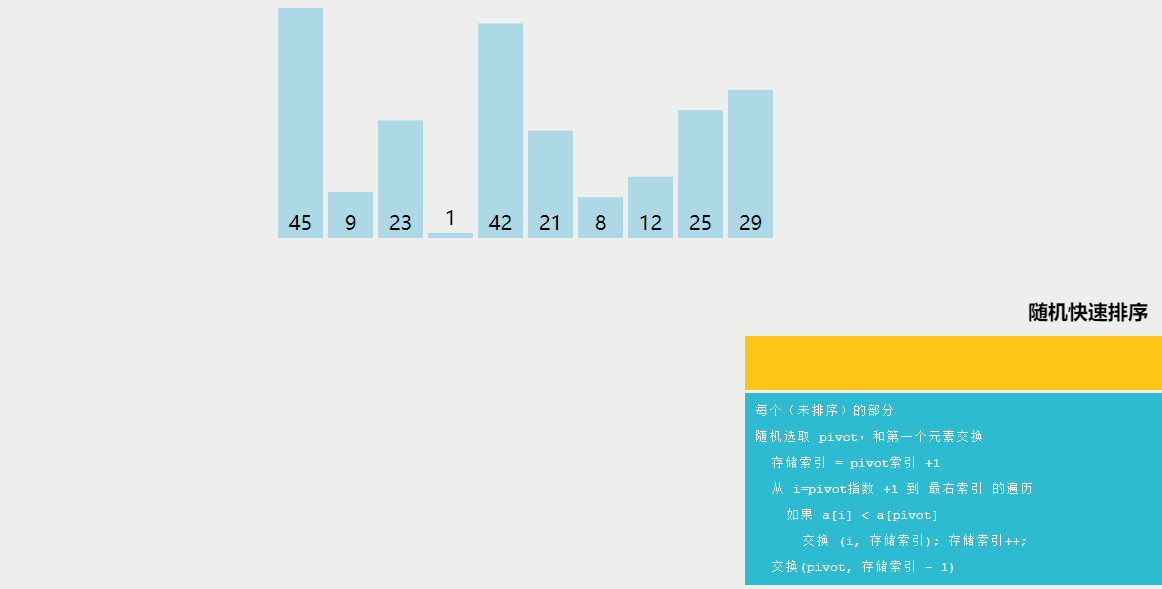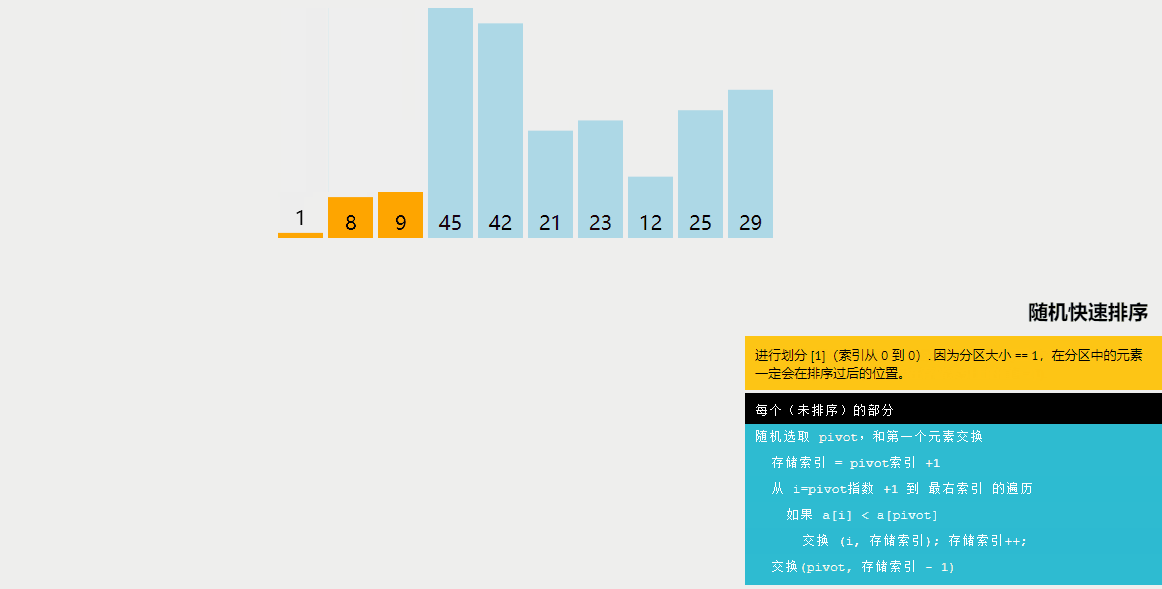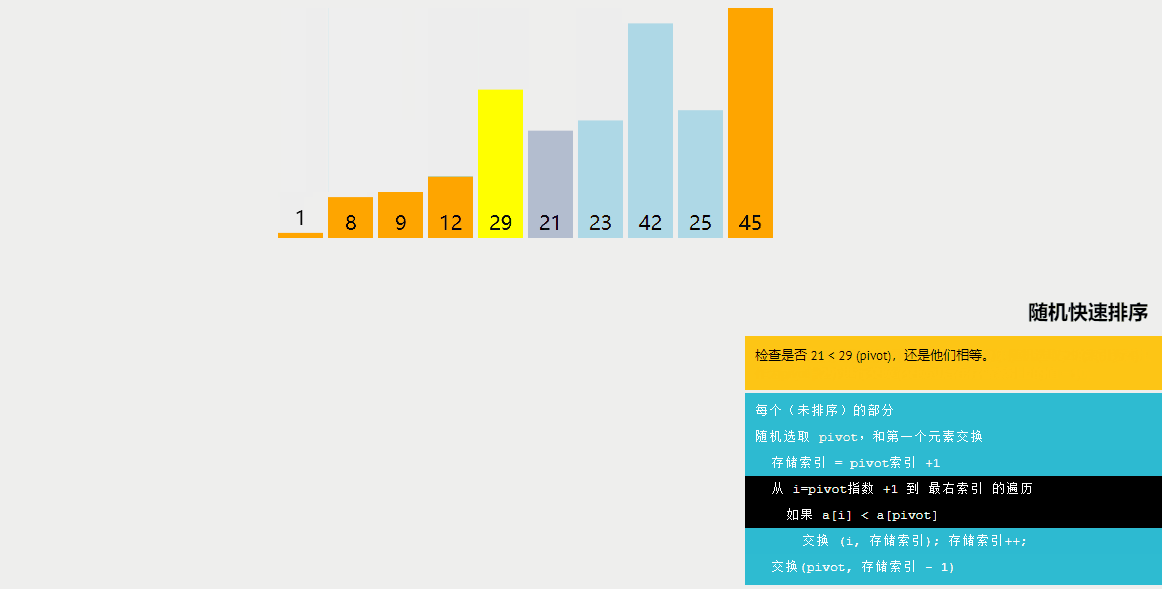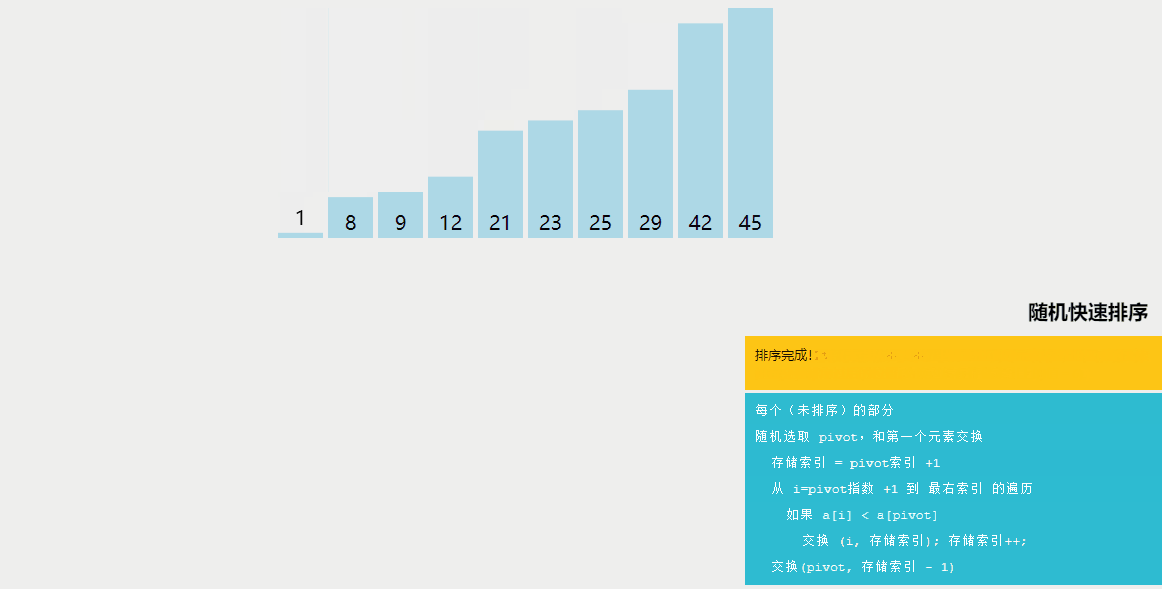
隨機快速排序與快速排序的區別:
快速排序是一種分治算法,通過選擇一個基準元素(通常是數組中的一個元素),將數組劃分為兩個子數組,一個子數組中的所有元素都小于基準元素,另一個子數組中的所有元素都大于基準元素。然后遞歸地對這兩個子數組進行排序。快速排序的平均時間復雜度為O(nlogn)。
隨機快速排序與快速排序的不同之處在于選擇基準元素的方式。在快速排序中,通常選擇數組的第一個或最后一個元素作為基準元素。而在隨機快速排序中,首先從數組中隨機選擇一個元素作為基準元素,然后進行劃分。
隨機快速排序的主要優點是減少了快速排序中最壞情況出現的概率。在快速排序中,如果選擇的基準元素是數組中的最小或最大元素,或者數組已經是有序的,那么劃分結果可能會非常不平衡,導致算法的時間復雜度接近O(n^2)。通過隨機選擇基準元素,可以有效地降低這種情況發生的概率,提高算法的平均性能。
因此,隨機快速排序相對于快速排序來說,具有更好的性能保證,尤其是在面對特定情況下的輸入數據時。它在實踐中通常被認為是快速排序的一種優化版本,可以提供更一致的性能,并減少最壞情況的發生概率。
時間復雜度:
- 最壞情況: O(n*n)
- 平均情況: O(n*logn)
- 最好情況: O(n*logn)
空間復雜度: O(logn)。
6、歸并排序
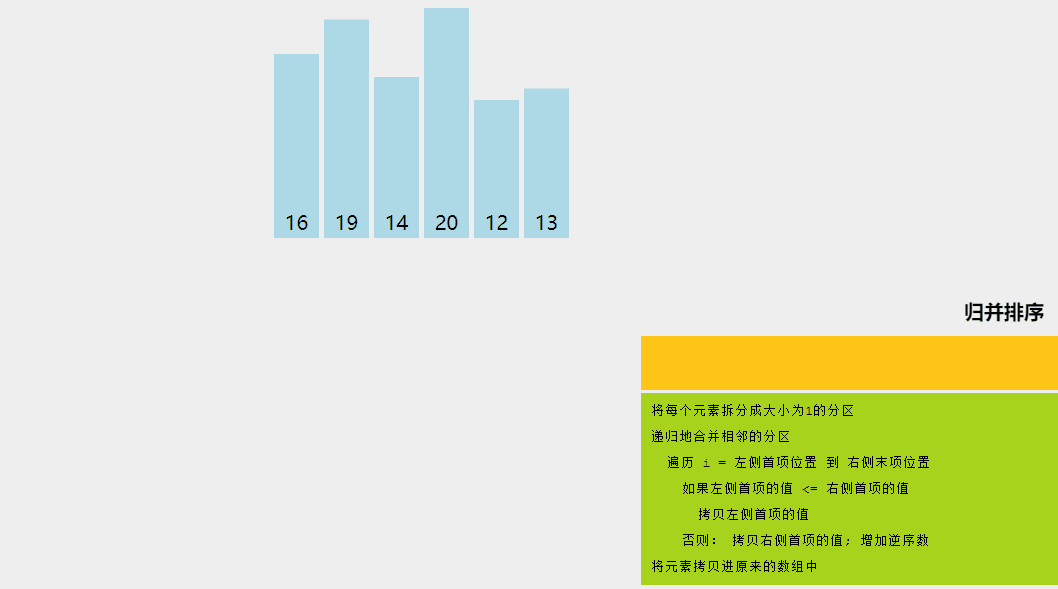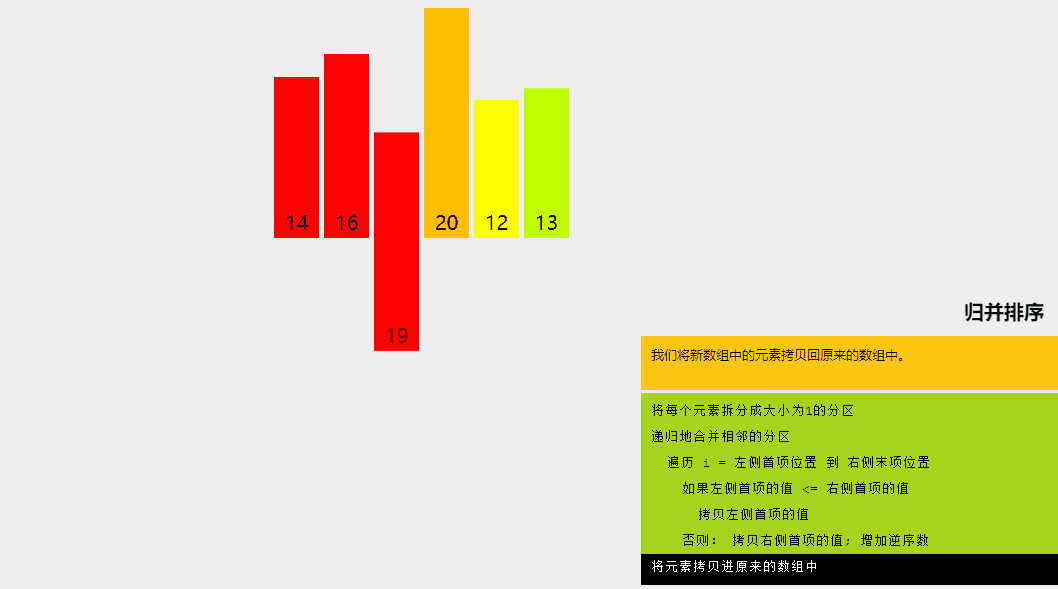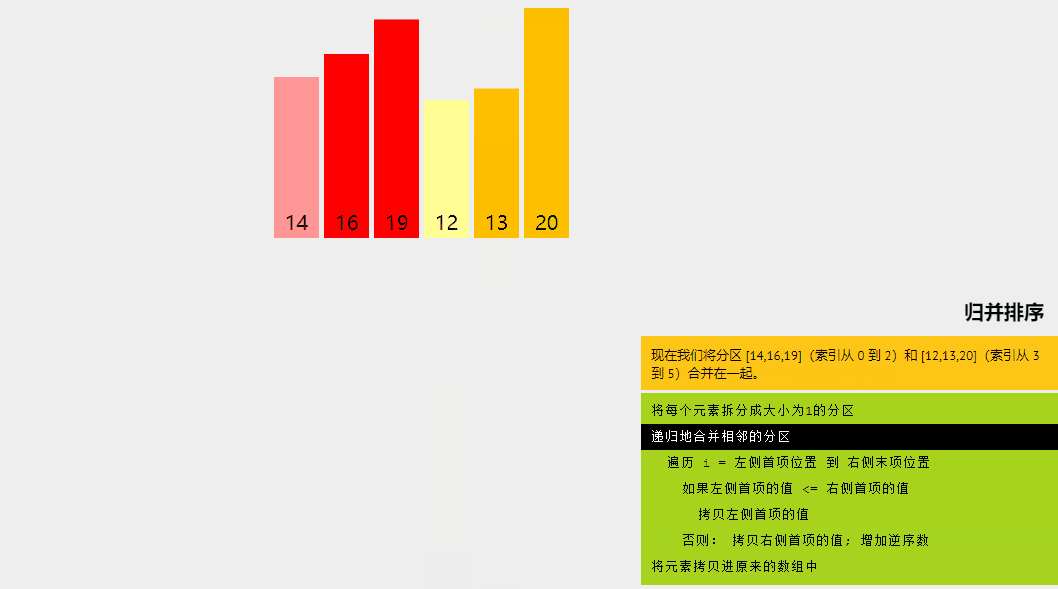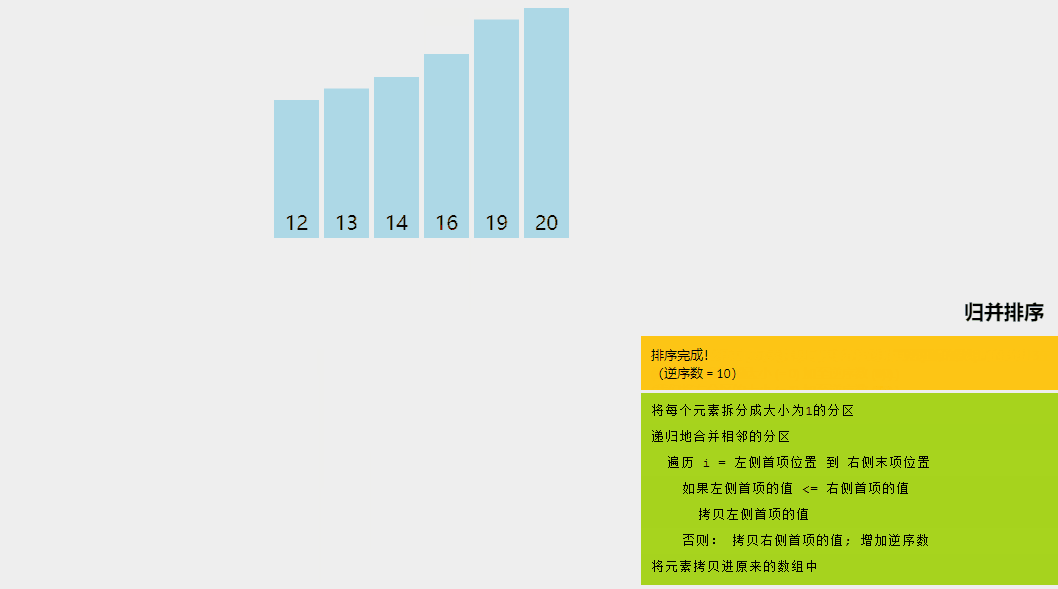
歸并排序是一種分而治之的算法。在每次迭代中,歸并排序將輸入數組劃分為兩個相等的子數組,為這兩個子數組遞歸地調用自身,最后合并已排序的兩半。
通過可視化了解合并排序算法。
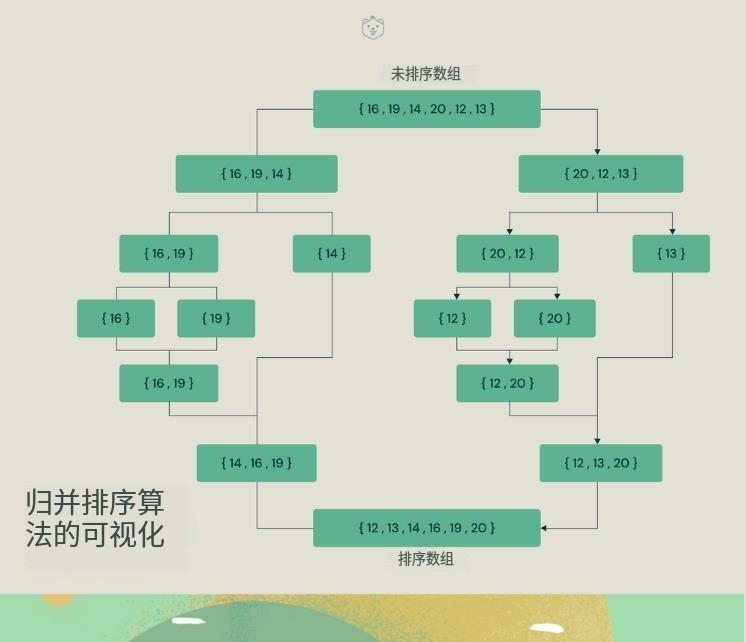
歸并排序算法解釋
看一下它的實現。
import java.util.Arrays;
public class MergeSort {
public static void merge(long[] arr, long lt, long m, long rt) {
long n1 = m - lt + 1;
long n2 = rt - m;
long[] L = new long[(int) n1];
long[] R = new long[(int) n2];
for (int i = 0; i < n1; i++)
L[i] = arr[(int) (lt + i)];
for (int j = 0; j < n2; j++)
R[j] = arr[(int) (m + 1 + j)];
int i = 0, j = 0;
int k = (int) lt;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
public static void mergeSort(long[] arr, long lt, long rt) {
if (lt >= rt)
return;
long m = lt + (rt - lt) / 2;
mergeSort(arr, lt, m);
mergeSort(arr, m + 1, rt);
merge(arr, lt, m, rt);
}
public static void printArray(long[] arr) {
for (int i = 0; i < arr.length; i++)
System.out.print(arr[i] + " ");
}
public static void main(String[] args) {
long[] arr = {16, 19, 14, 20, 12, 13};
System.out.print("Unsorted array is: ");
printArray(arr);
mergeSort(arr, 0, arr.length - 1);
System.out.print("\nSorted array is: ");
printArray(arr);
}
}歸并排序的實現
時間復雜度:
- 最壞情況: O(n*logn)
- 平均情況: O(n*logn)
- 最好情況: O(n*logn)
空間復雜度: O(n)。
7、計數排序
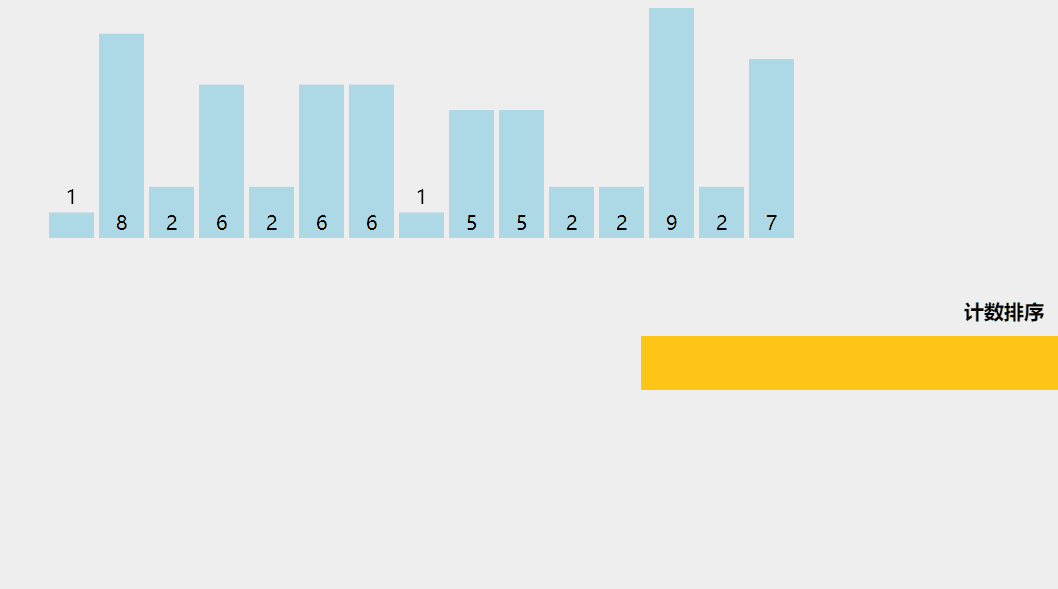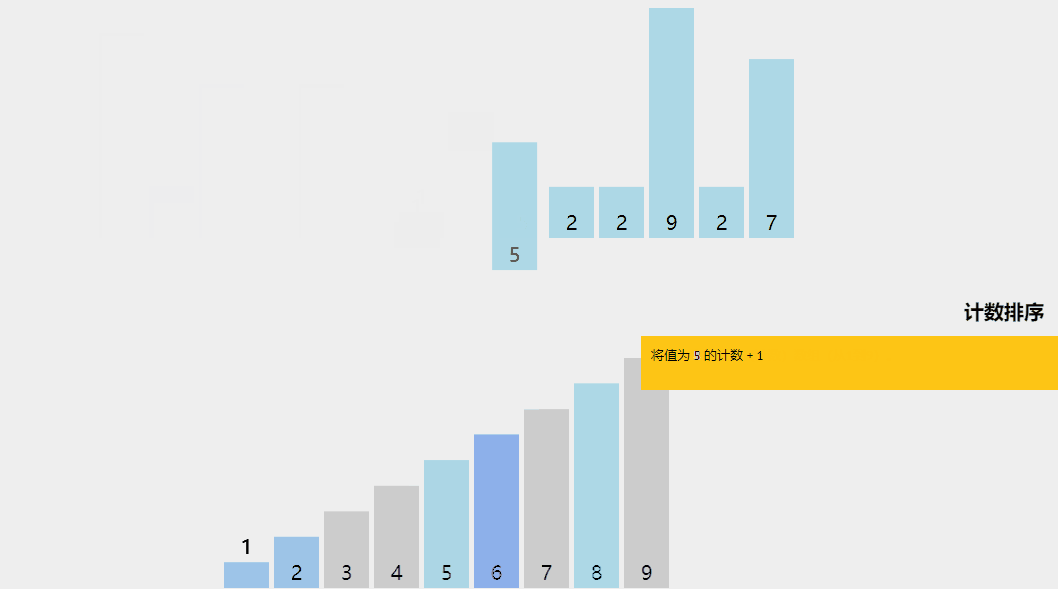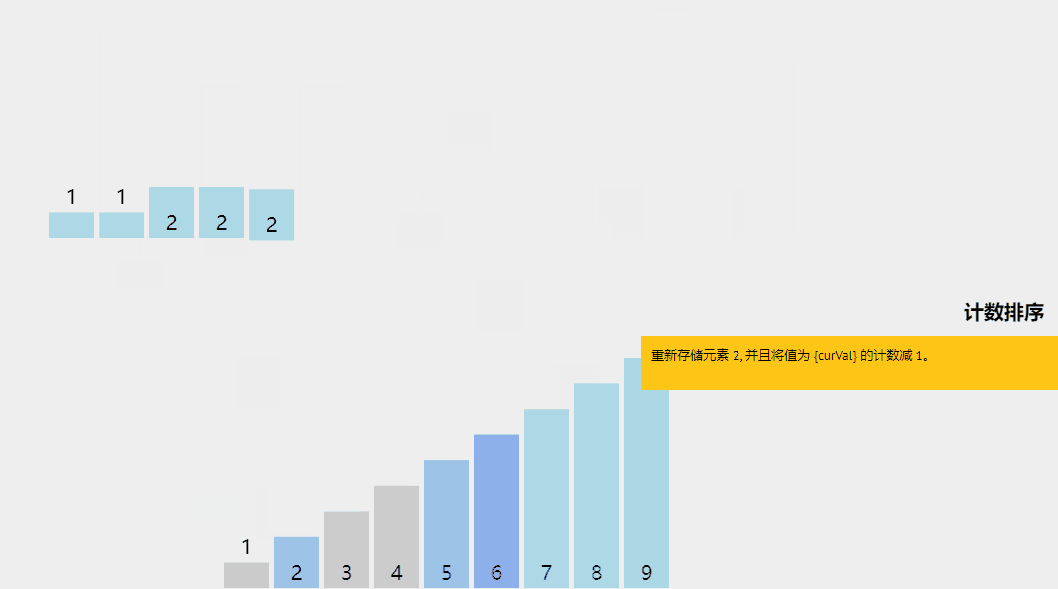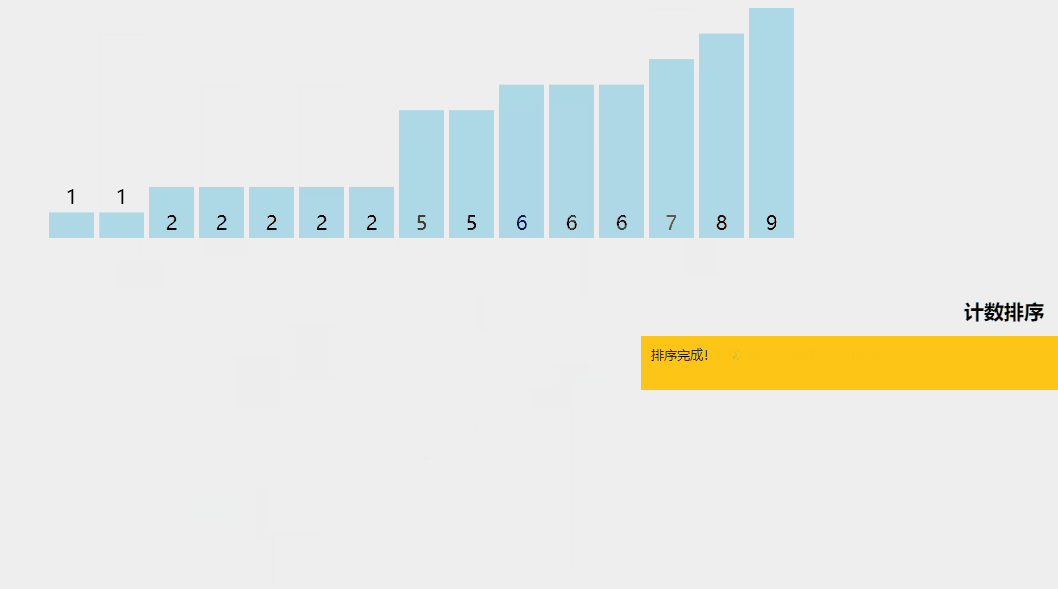
計數排序是一種有趣的排序技術,主要是因為它關注特定范圍內唯一元素的頻率(類似于散列)。
它的工作原理是計算具有不同鍵值的元素數量,然后在計算未排序序列中每個唯一元素的位置后構建排序數組。
它與上面列出的算法不同,因為它實際上涉及輸入數據元素之間的零比較!
通過示例了解計數排序算法。

計數排序算法解釋
現在繼續看一下它在 Java 中的實現。
import java.util.Scanner;
public class CountSort {
public static void print(long[] vec, long n) {
for (long i = 1; i <= n; i++)
System.out.print(vec[(int) i] + " ");
System.out.println();
}
public static long getMax(long[] vec, long n) {
long max = vec[1];
for (long i = 2; i <= n; i++) {
if (vec[(int) i] > max)
max = vec[(int) i];
}
return max;
}
public static void countSort(long[] vec, long n) {
long[] output = new long[(int) (n + 1)];
long max = getMax(vec, n);
long[] count = new long[(int) (max + 1)];
for (int i = 0; i <= max; i++)
count[i] = 0;
for (long i = 1; i <= n; i++)
count[(int) vec[(int) i]]++;
for (int i = 1; i <= max; i++)
count[i] += count[i - 1];
for (long i = n; i >= 1; i--) {
output[(int) count[(int) vec[(int) i]]] = vec[(int) i];
count[(int) vec[(int) i]] -= 1;
}
for (long i = 1; i <= n; i++) {
vec[(int) i] = output[(int) i];
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("Enter the size of array: ");
long n = scanner.nextLong();
long[] arr = new long[(int) (n + 1)];
System.out.println("Enter elements:");
for (long i = 1; i <= n; i++)
arr[(int) i] = scanner.nextLong();
System.out.print("Unsorted array: ");
print(arr, n);
countSort(arr, n);
System.out.print("Sorted array: ");
print(arr, n);
scanner.close();
}
}計數排序實現
時間復雜度:
- 最壞情況: O(n+k),其中 n 是輸入數組的大小,k 是數組中唯一元素的數量。
空間復雜度: O(n+k)。
8、基數排序

正如之前所看到的,計數排序之所以與眾不同,是因為它不是像合并排序或冒泡排序那樣基于比較的排序算法,從而將其時間復雜度降低到線性時間。
但是,如果輸入數組的范圍從 1 到 n^2,計數排序就會失敗,在這種情況下,其時間復雜度會增加到 O(n^2)。
基數排序背后的基本思想是擴展計數排序的功能,以便在輸入數組元素范圍從 1 到 n^2 時獲得更好的時間復雜度。
通過示例了解基數排序。
算法:
對于每個數字 i,其中 i 從數字的最低有效數字到最高有效數字變化,根據第 i 個數字使用計數排序算法對輸入數組進行排序。請記住,我們使用計數排序,因為它是一種穩定的排序算法。
例子:

基數排序算法解釋
因此,我們觀察到基數排序在整個執行過程中使用計數排序作為其子例程。現在看一下它的 Java實現。
import java.util.Arrays;
public class RadixSort {
public static void getMax(long[] vec, int n) {
long maxval = vec[0];
for (int i = 1; i < n; i++) {
if (vec[i] > maxval) {
maxval = vec[i];
}
}
}
public static void countSort(long[] vec, int n, long x) {
long[] res = new long[n];
long[] count = new long[10];
Arrays.fill(count, 0);
for (int i = 0; i < n; i++) {
count[(int)((vec[i] / x) % 10)]++;
}
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
for (int i = n - 1; i >= 0; i--) {
res[(int)(count[(int)((vec[i] / x) % 10)] - 1)] = vec[i];
count[(int)((vec[i] / x) % 10)]--;
}
for (int i = 0; i < n; i++) {
vec[i] = res[i];
}
}
public static void radixSort(long[] vec, int n) {
long m = vec[0];
for (int i = 1; i < n; i++) {
if (vec[i] > m) {
m = vec[i];
}
}
for (long x = 1; m / x > 0; x *= 10) {
countSort(vec, n, x);
}
}
public static void main(String[] args) {
long[] vec = { 53, 89, 150, 36, 633, 233 };
int n = vec.length;
radixSort(vec, n);
for (int i = 0; i < n; i++) {
System.out.print(vec[i] + " ");
}
}
}基數排序實現
時間復雜度: O(d(n+b)),其中b代表數組元素的基數(例如- 10代表十進制)
空間復雜度: O(n+d),其中 d 是數組元素中的最大位數。
總結
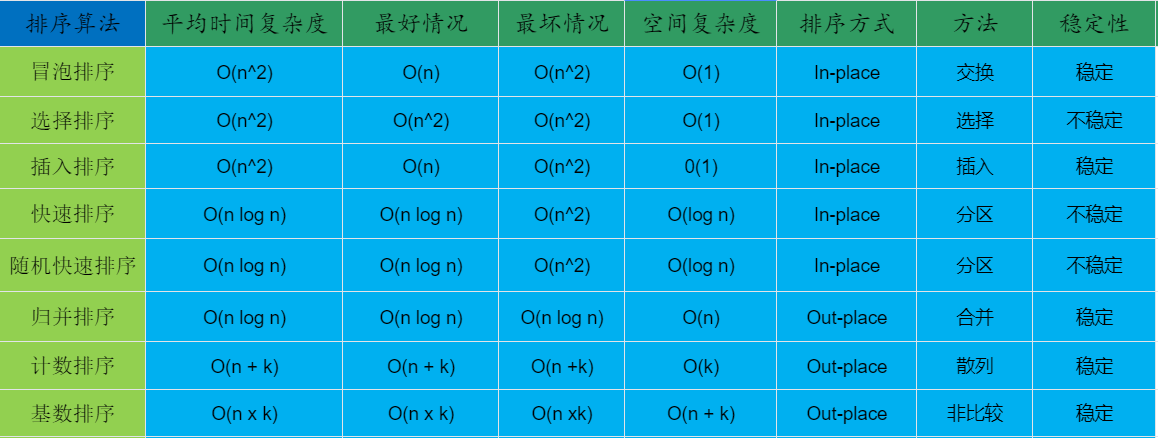
排序算法總結
名詞解釋:
- n:數據規模
- k:“桶”的個數
- In-place:占用常數內存,不占用額外內存
- Out-place:占用額外內存
- 穩定性:排序后 2 個相等鍵值的順序和排序之前它們的順序相同