要讓大型語言模型（LLM）充分發揮其能力，有效的 prompt 設計方案是必不可少的，為此甚至出現了 prompt engineering（提示工程）這一新興領域。

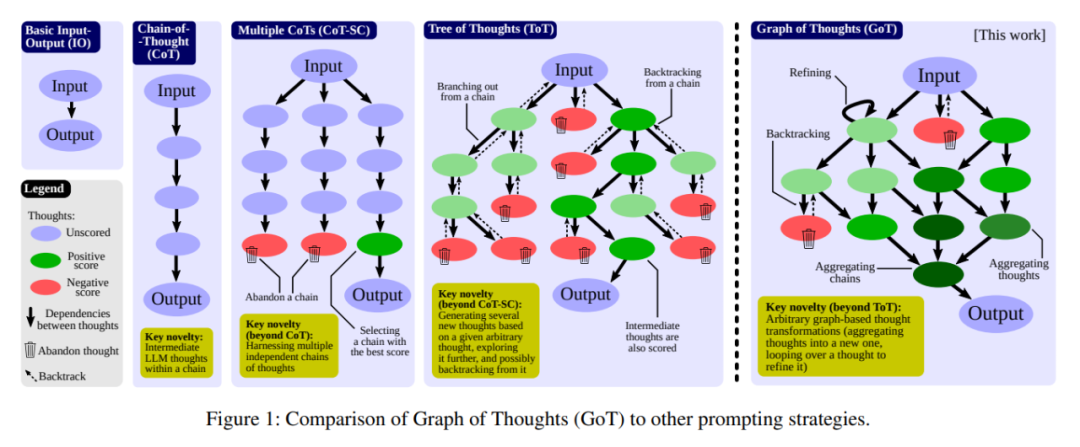
在各種 prompt 設計方案中，思維鏈（CoT）憑借其強大的推理能力吸引了許多研究者和用戶的眼球，基于其改進的 CoT-SC 以及更進一步的思維樹（ToT）也收獲了大量關注。

近日，蘇黎世聯邦理工學院、Cledar 和華沙理工大學的一個研究團隊提出了更進一步的想法：思維圖（GoT）。讓思維從鏈到樹到圖，為 LLM 構建推理過程的能力不斷得到提升，研究者也通過實驗證明了這一點。他們也發布了自己實現的 GoT 框架。

研究論文：https://arxiv.org/pdf/2308.09687v2.pdf

官方實現：https://github.com/spcl/graph-of-thoughts

論文概覽

大型語言模型正在變成人工智能世界的主導技術。近些年高速發展的模型主要基于僅解碼器 Transformer 的變體，比如 GPT、PaLM 或 LLaMA。

而在解決不同的 LLM 任務時，prompt 工程設計是一種能高效利用資源的方法。簡單來說，就是在發送給 LLM 的輸入中包含對任務的描述。如果能以適當的形式描述該任務，那么 LLM 就能借助其用于生成文本的基于自回歸 token 的機制來解決該任務。這樣的 prompt 可能包含帶有解答的示例任務（少樣本 prompt 設計，也被稱為上下文學習（ICL），也可能完全不包含示例任務（零樣本 prompt 設計）。近些年的研究和應用表明，這一機制可用于解決涉及數學、常識或符號推理的多種類型的任務。

思維鏈（CoT）便是一種用于設計 prompt 的方法，即 prompt 中除了有任務的輸入和輸出外，還包含推理的中間步驟（中間思維）。研究表明，CoT 能極大地提升 LLM 的能力，使之無需任何模型更新便能解決一些難題。

也有研究者改進了 CoT，提出了使用 CoT 實現自我一致的方法（CoT-SC）；這個方案是生成多個 CoT，再選出其中最佳的結果。

最近還有研究者更進一步提出了思維樹（ToT），其做法是通過樹（tree）來建模 LLM 推理過程。這能讓模型使用不同的思維路徑，并能提供全新的功能，比如基于不好的結果反向回溯推理過程。不幸的是，由于 ToT 方法為思維過程強加了嚴格的樹結構，所以會極大限制 prompt 的推理能力。更多詳情請參閱機器之心文章《思考、思考、思考不停歇，思維樹 ToT「軍訓」LLM》。

蘇黎世聯邦理工學院、Cledar 和華沙理工大學的這個研究團隊認為，如果能將 LLM 的思維構建成任意的圖結構，那么就能為 prompt 的能力帶來重大提升。他們表示，這一想法受到了多種現象的啟發，比如人類的推理方式、大腦結構和算法的執行方式。

在進行思考時，人類不會像 CoT 那樣僅遵循一條思維鏈，也不是像 ToT 那樣嘗試多種不同途徑，而是會形成一個更加復雜的思維網。舉個例子，一個人可能會先探索一條思維鏈，然后回溯再探索另一條，然后可能會意識到之前那條鏈的某個想法可以和當前鏈結合起來，取長補短，得到一個新的解決方案。類似地，大腦會形成復雜的網絡，呈現出類似圖的模式，比如循環模式。算法執行時也會揭示出網絡的模式，這往往可以表示成有向無環圖。

研究者表示，如果將這種對應的圖使能的變換用于 LLM 思維，那么有望創造一種強大的設計 prompt 的方法，但這種變換無法通過 CoT 或 ToT 自然地表達出來。

然后他們觀察到：如果將 LLM 的推理過程建模成圖，那么就能自然地實現這些以及其它許多思維變換。基于這一觀察，他們提出了思維圖（GoT/Graph of Thoughts），這種方法可以通過網絡形式的推理來增強 LLM 的能力。

在 GoT 中，一個 LLM 思維會被建模成一個頂點，頂點之間的依賴關系則建模為邊。使用 GoT，通過構建有多于一條輸入邊的頂點，可以將任意思維聚合起來。整體而言，GoT 使用的圖抽象方法可無縫地將 CoT 和 ToT 泛化到更復雜的思維模式，而且這個過程無需更新模型。

然而，要實際實現 GoT，還需要解決一些設計上的挑戰。比如，對于不同的任務，最佳的圖結構是什么樣的？為了最大化準確度和最小化成本，聚合思維的最好方法是什么？

為了解答這些問題以及更多其它問題，這些研究者設計了一種實現 GoT 的模塊化架構。該設計有兩大亮點。

一是可實現對各個思維的細粒度控制。這讓用戶可以完全控制與 LLM 進行的對話并使用先進的思維變換，比如將正在進行的推理中兩個最有希望的思維組合起來得到一個新的。

二是這種架構設計考慮了可擴展性 —— 可無縫地擴展用于新的思維變換、推理模式（即思維圖）和 LLM 模型。這讓用戶可使用 GoT 快速為 prompt 的新設計思路構建原型，同時實驗 GPT-3.5、GPT-4 或 Llama-2 等不同模型。

研究者也展現了 GoT 的一些用例（排序、摘要的關鍵詞計數、集合運算、文檔合并），他們還詳細說明了如何使用基于圖的范式來實現它們。他們通過實驗評估了 GoT，展現了其相對于其它當前最佳方法的優勢。

研究者表示，整體而言，GoT 尤其適用于可自然分解成更小子任務的任務，并且這些子任務可以分開解決，然后融合成一個最終解答。在這方面，GoT 的表現優于其它方案，比如在排序任務上，GoT 分別優于 CoT 和 ToT 約 70% 和 62%，同時成本還比 ToT 低 31% 以上。

表 1 給出了 GoT 與其它 prompt 設計方案的定性比較。GoT 是唯一一種能在一個 prompt 內實現任意基于圖的思維變換的方案（比如聚合），從而能將之前的所有方案囊括進來。

他們還有另一項貢獻，即提出一種新的評估指標 —— 思維容量（the volume of a thought），可用于評估 prompt 設計策略。研究者表示，使用這一指標的目標是更好地理解 prompt 設計方案之間的差異。

對于一個給定的思維 v，v 的容量是指 LLM 思維的數量，用戶可以基于此使用有向邊得到 v。直觀上說，這些就是有望對 v 做出貢獻的所有 LLM 思維。

作者通過研究表明，通過整合聚合等思維變換技術，GoT 能讓思維容量比其它方案顯著更大。

GoT 框架

下面詳細介紹一下 GoT 框架。其示意圖見圖 1，圖中還給出了其它 prompt 設計策略的示意圖。

在數學形式上，GoT 可以建模為一個元組 (G, T, E, R)，其中 G 是 LLM 推理過程（即上下文中的所有 LLM 思維及其關系），T 是可能的思維變換，E 是用于獲得思維分數的評估器函數，R 是用于選擇最相關思維的排序函數。

推理過程

這里，推理過程被建模為一個有向圖 G = (V, E)，其中 V 是一組頂點，E ? V × V 是一組邊。G 是有向的，因此邊是有序頂點對 E ? V × V 的子集。一個頂點包含對當前問題的一個解答，不管這個問題是最初的問題、還是中間問題或最后的問題。這種思維的具體形式取決于用例；其可能是一段文本（在寫作任務中），也可能是一個數值序列（在排序任務中）。有向邊 (t_1, t_2) 表示思維 t_2 的構建方式是將 t_1 用作「直接輸入」，即通過明確指示 LLM 使用 t_1 來生成 t_2。

在某些用例中，圖節點屬于不同類別。舉個例子，在寫作任務中，某些頂點建模寫出一段文本的計劃，其它節點則建模實際的文本段。在這種情況下，GoT 采用異構圖 G = (V, E, c) 來建模 LLM 推理，其中 c 將頂點 V 映射到各自的類 C（在上述案例中，C = {plan, par} ）。這樣一來，任何頂點 v 都可以建模推理的不同方面。

于是 G 就與 LLM 推理過程關聯了起來。為了推進這一過程，用戶可對 G 使用思維變換。舉個這種變換的例子：將目前為止分數最高的思維融合成一個新的。另一個例子是對一個思維進行循環，以對其增強。注意，這些變換嚴格擴展了 CoT、CoT-SC 或 ToT 中可用轉換的集合。

思維變換

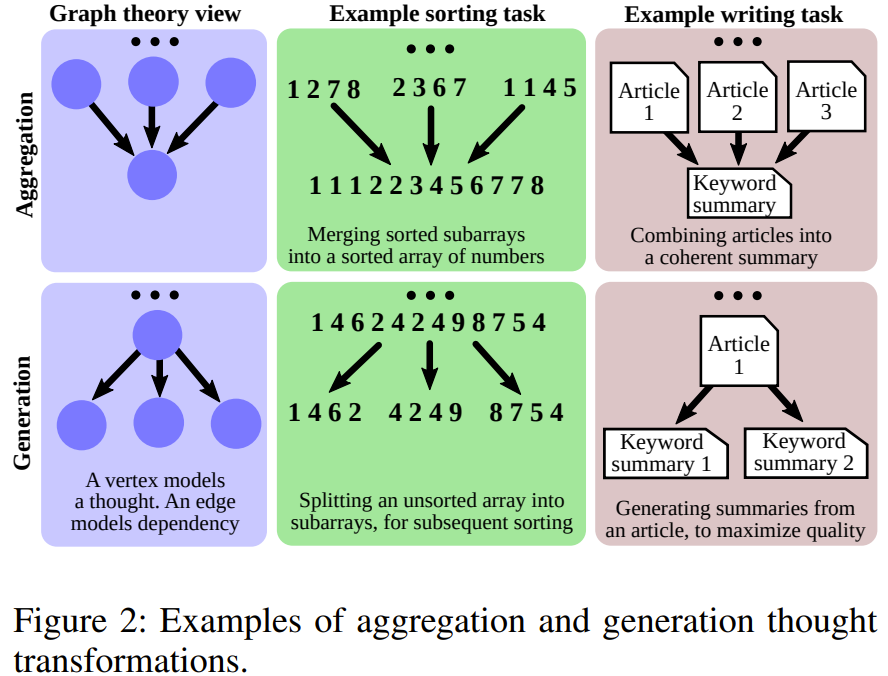
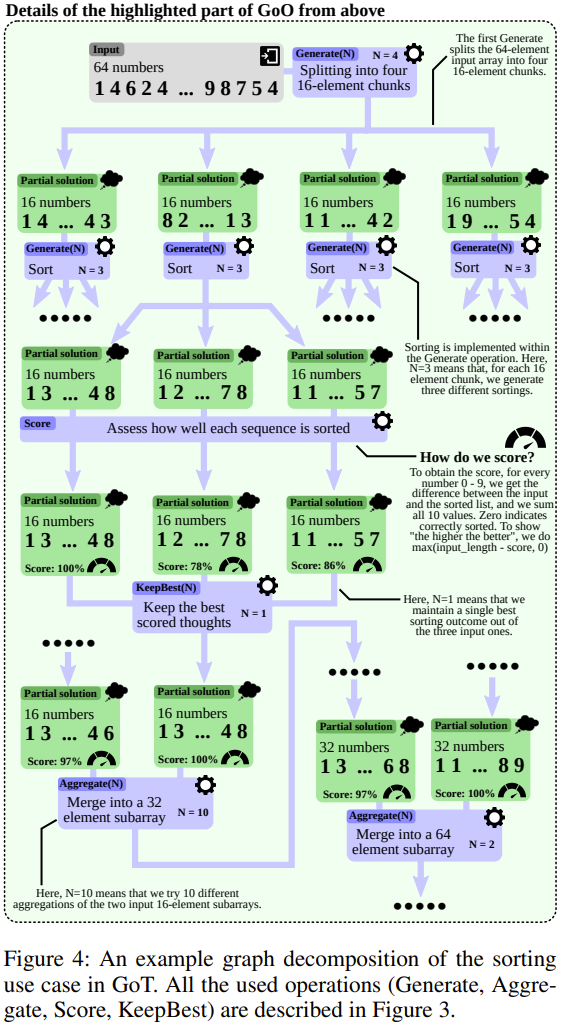
得益于將基于圖的模型用于推理，GoT 能實現全新的思維變換。研究者稱之為圖使能的變換（graph-enabled transformation）。比如，在寫作任務中可以將多篇輸入文章組合成一篇連貫一致的摘要。在排序時，可將多個已排序的數值子數組合并為一個最終已排序數組。圖 2 給出了聚合和生成的示例。

從數學形式上講，每個這樣的變換都可以建模成 T (G, p_θ)，其中 G = (V, E) 是反映推理當前狀態的圖，p_θ 是所使用的 LLM。T 修改 G 的方式通常是通過添加新頂點及其傳入邊。于是有 G′ = T (G, p_θ) = (V′, E′)，其中 V′ = (V ∪ {V^+}) \ {V^?} 且 E′ = (E ∪ {E^+}) \ {E^?}。V^+ 和 E^+ 是注入到 G 中的新頂點和邊，它們分別建模的是新的思維和它們的依賴關系。

為了最大化 GoT 的表達能力，用戶還可以刪除思維，做法是指定要刪除的相應頂點和邊（分別為 V^? 和 E^?）。在這里，確保集合 V^+、E^+、V^? 和 E^? 有一致的變換是用戶的責任（舉個例子，用戶不會嘗試刪除不存在的頂點）。這使得 prompt 方案能無縫整合，其中用戶可以為了節省上下文中的空間而移除無法帶來提升的推理部分。

T 的具體形式及其影響 G 的方式取決于具體的變換。下面首先詳細介紹主要幾個圖使能的思維變換，然后會描述 GoT 何以囊括之前方案的變換。除非另有說明，V^? = E^? = ?。

聚合變換：用戶可以使用 GoT 將任意思維聚合成新思維，實現取長補短。這里看看只創建一個新頂點的基礎形式：V^+ = {v^+} 且 E^+ = {(v_1, v^+), ...,(v_k, v^+)}，其中 v_1, ..., v_k 是被融合的 k 個思維。更一般而言，這能實現對推理路徑的聚合，即更長的思維鏈，而不只是單個思維。使用圖模型，可以輕松實現聚合變換：通過添加來自建模了幾條鏈中最后思維的頂點 v_1, ..., v_k 的傳出邊，使之指向組合這些鏈的單個思維 v^+。

細化變換：另一種思維變換是通過修改內容對當前思維 v 進行細化：V^+ = {} 和 E^+ = {(v, v)}。圖中的這個循環表示與原始思維有同樣連接的迭代版思維。

生成變換：最后，用戶還可以基于已有的單個思維 v 生成一個或多個新思維。這一類別中包含 ToT 或 CoT-SC 等更早期方案中的類似推理步驟。從數學形式上講，有 

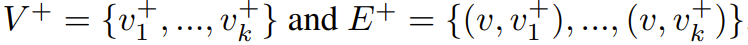
對思維進行評分和排名

對思維評分的目的是為了理解當前的解答是否足夠好。分數被建模為一個一般函數 E (v, G, p_θ)，其中 v 是所要評估的思維。為了盡可能讓 E 更普適通用，E 中還使用了推理的整個過程 (G)，因為在某些評估場景中，分數可能與其它思維相關。

GoT 也能排名。研究者使用了函數 R (G, p_θ, h) 來建模，其中 h 指定了要被 R 返回的 G 中排名最高的思維的數量。雖然 R 的具體形式取決于用例，但最常使用一個簡單而有效的方法是返回分數最高的 h 個思維，即 v_1, ..., v_h = R (G, p_θ, h)。

E 和 R 的具體形式取決于用例。

系統架構和擴展能力

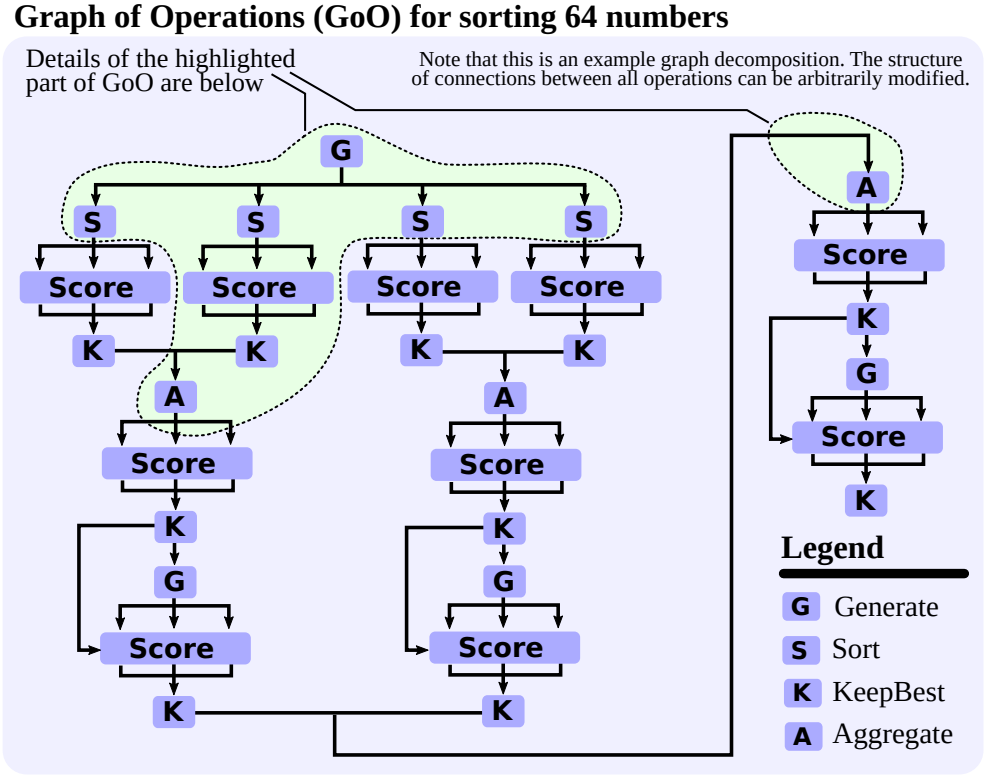
GoT 由一組交互式模塊構成，見圖 3（藍色部分）。這些模塊是 Prompter（準備用于 LLM 的消息）、Parser（解析器，提取 LLM 答復中的信息）、評分模塊（驗證 LLM 答復并評分）、Controller（控制器，協調整個推理過程，并決定如何推進推理）。Controller 中包含另外兩個重要組件：操作圖（GoO）和圖推理狀態（GRS）。GoO 是一個靜態結構，其指定了對給定任務的圖分解，即它規定了應用于 LLM 思維的變換及其順序和依賴關系。GRS 是一個動態結構，其維持著正在進行的 LLM 推理過程的狀態（其思維及其狀態的歷史）。

用例示例

研究者描述一些 GoT 的一些用例，包括排序、集合運算、關鍵詞計數、文檔合并；下圖 4 便是 GoT 的排序用例中一個圖分解示例。這里我們不對用例做詳細介紹，詳情參閱原論文。

延遲與容量的權衡

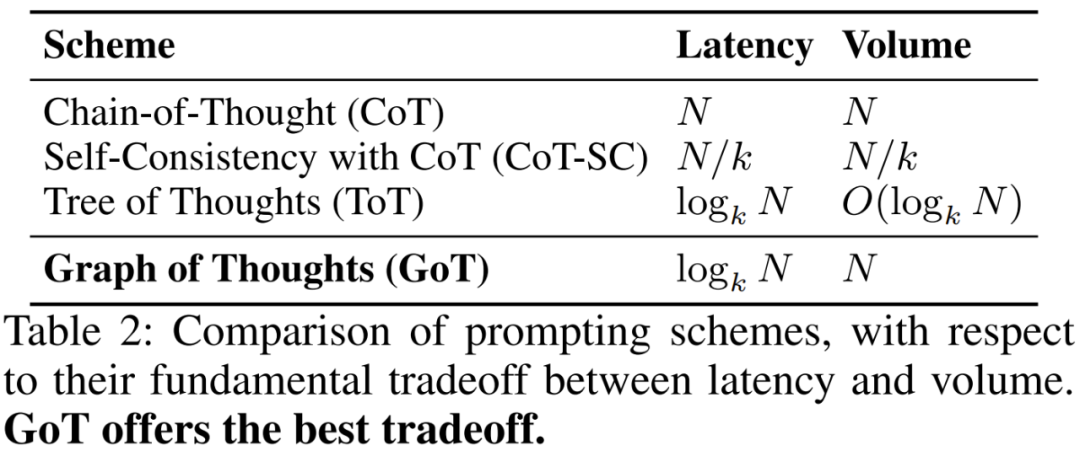
延遲（在思維圖中抵達給定最終思維的跳數）和容量之間的權衡也非常重要，研究者表明：GoT 在這一權衡上也優于之前的 prompt 設計方案。這篇論文定義了一個新指標 —— 思維容量，即可以影響給定思維 t 的之前 LLM 思維的數量。從數學上看，思維 t 的容量就是在思維圖中，與 t 之間存在路徑的思維的數量。研究者假設輸出單個思維的成本為 O (1)，并將每個提示方案的總成本固定為 Θ(n)。

各種方案的結構如下。CoT-SC 由源自單個起始思維的 k 條獨立鏈構成。ToT 是一條完全 k 叉樹。而在 GoT 中，會在其葉節點處加入一個完全 k 叉樹，并帶有一個「鏡像」k 叉樹 —— 其大小一樣而邊是反向的。

詳細分析見表 2。CoT 的容量較大，最大可至 N，但也有 N 的高延遲成本。CoT-SC 將延遲降低了 k 倍（對應于其分支因子），但同時其容量也會減小 k 倍。ToT 的延遲為 log_k N，但容量也很低。GoT 是唯一能做到低延遲 log_k N 和高容量 N 的方案。GoT 之所以能做到這一點，是因為其利用了思維聚合，使其可從圖分解中任何其它中間思維得到最終思維。

評估

研究者通過實驗展現了 GoT 相對于其它方案的優勢。其中重點比較的是 GoT 和 ToT，因為 ToT 的表現已經優于其它方案了。當然，他們也還是用 IO、CoT 和 CoT-SC 做了些實驗。

圖 5（排序）、6（集合交集）、7（關鍵詞計數）、8（文檔合并）展示了實驗結果。

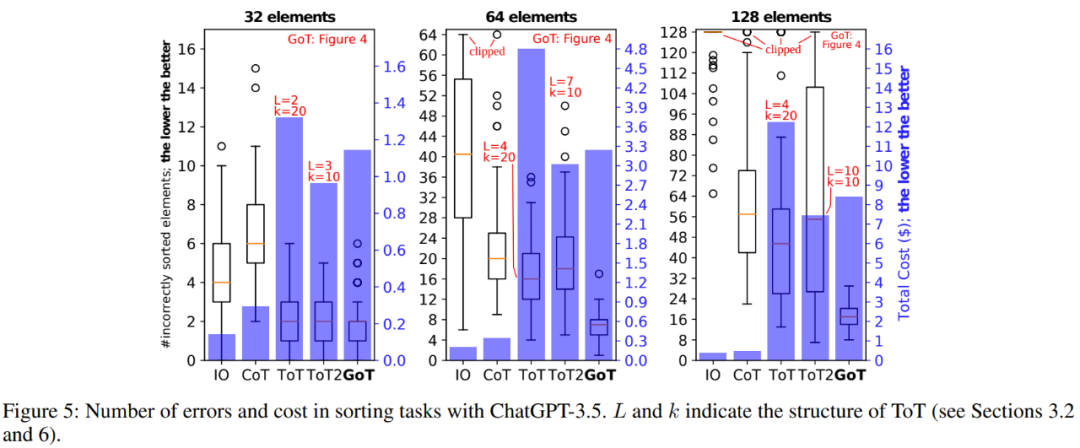
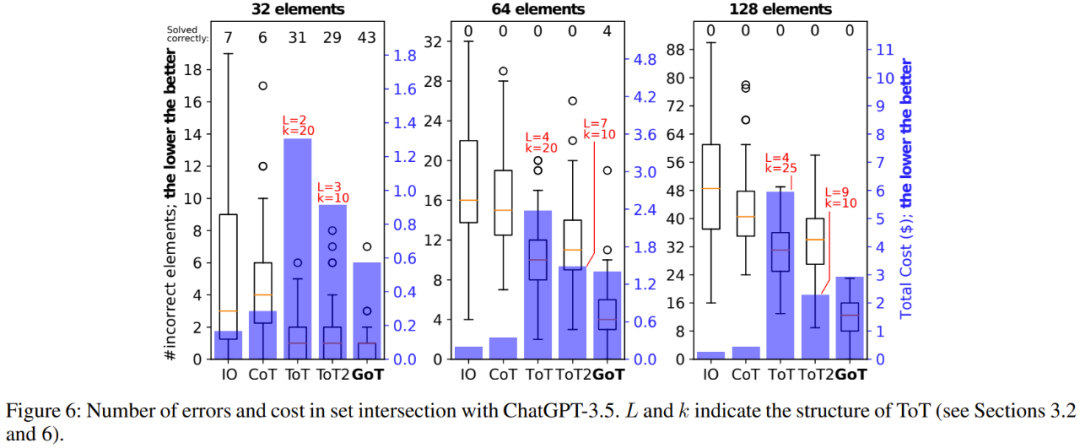
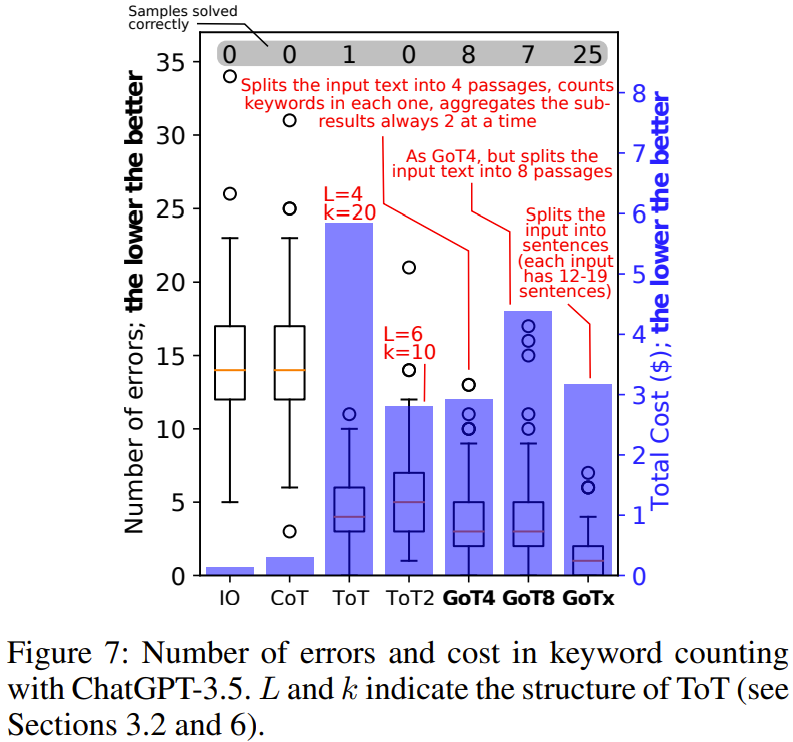
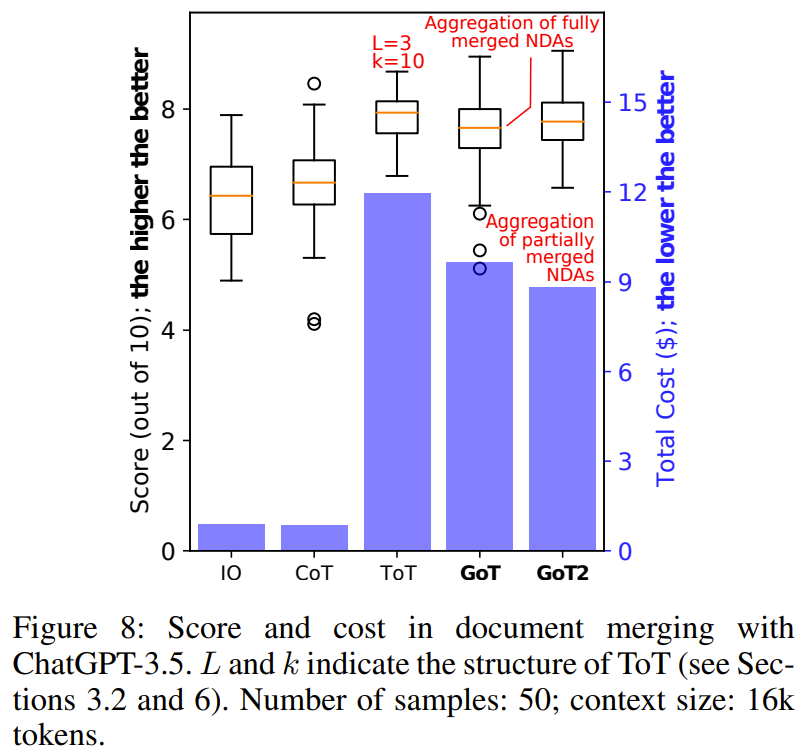
總體而言，在實驗評估過的所有基準上，GoT 的輸出質量都優于 ToT，并且還實現了更低的推理成本。