手寫圖表指南，你學會了嗎？

作者：強敏 2023-01-30 09:01:54

大數據數據可視化

說到數據可視化，大家應該都不陌生。它旨在借助于圖形化手段，清晰有效的傳達與溝通信息。廣義的數據可視化涉及信息技術、自然科學、統計分析、圖形學等多種學科。

1、前言

圖例來源網絡

我們熟知的圖形、圖表以及地圖等都屬于數據可視化的范疇。今天我們主要討論數據可視化中的圖表，像柱狀圖、折線圖、面積圖、餅圖、熱力圖都是使用頻率非常高的圖表。

圖例來源網絡

如果要在移動端繪制一個類似于下圖，使用真實數據渲染的簡單面積圖表，我們應該如何實現它呢？相信大家腦子里應該都有各種方案了，那么接下來我們就來一步步實現它。

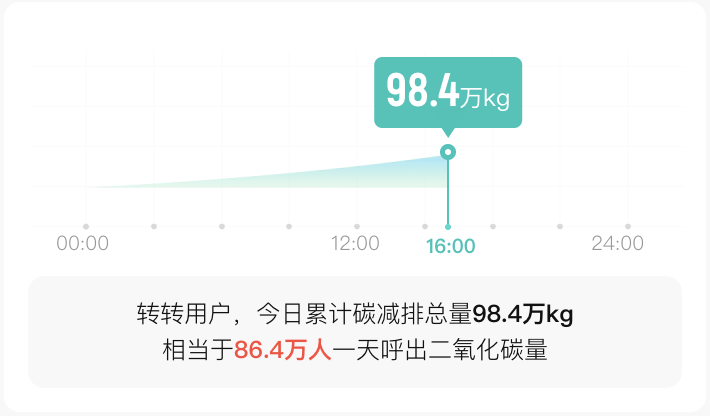
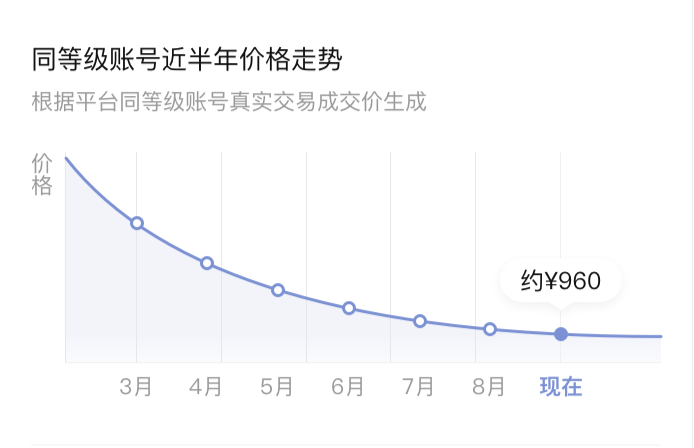
2、技術選型

需求

圖表樣式定制化圖表樣式為我司設計師獨立設計，最終實現效果應該做到100%還原設計細節；
交互效果默認情況下數據游標只顯示當前數據點，如需查看其他月份或者時刻數據，需要用戶手動點擊切換；
曲線面積圖最終需要繪制出一個面積圖，也就是用真實數據繪制出的曲線與坐標軸相交而形成的一個區域；

明確了具體的需求之后，我們就可以考慮技術方案選型了。

2.1 圖表庫

目前業界有很多成熟的圖表庫，像我們熟知的highcharts、echarts，Bizcharts，G2，更高階的three.js等等。如果采用現有圖表庫來實現上述圖表的話，會存在以下一些問題。

無法100%還原圖表樣式
包體積大，引入會造成項目性能問題

引入現有圖表庫的方案固然非常簡單，大大節省了前端同學的開發量。但是存在著以上兩個比較突出的問題。

圖表庫的圖表樣式都是通過配置完成，實現出來的效果在某些細節上難以完全還原設計稿，并且翻文檔測試配置項的過程也比較繁瑣。而且如果后續設計同學需要優化圖表樣式，并且此優化難以通過現有圖表庫配置項實現的話，那可能就需要二次開發圖表庫，對我們來說，也是一個不小的工作量；

通常C端的圖表需求并不是那么通用，可能一個項目也就實現這么一兩個圖表，如果引入圖表庫的話，對項目本身來說，無形中又增加了一些打包成本。那有些同學可能會說，現在的某些圖表庫已經可以按需引用了，這樣增加打包體積這個問題可能就不是問題了，雖然現在的某些比較成熟的圖表庫可以按需引用，但是在引用某個圖表文件之前還是要引入一些核心文件，這些核心文件依然會占據不小的包體積。總結來說，引入現有圖表庫的方案成本高、靈活性差。

2.2 canvas

canvas相信對每一個前端開發者來說都不陌生，如果我們采用canvas來繪制圖表的話，有兩個問題比較棘手，上文中有提到過，我們要實現的圖表是有交互效果的，當用戶點擊數據點的時候，則需要顯示當前數據點的數據游標，再點擊其他數據點的時候，數據游標也要相應的切換。大家都知道，使用原生canvas來實現事件系統異常麻煩，并且canvas的重繪機制也是我非常不喜歡的一點。總結一下，原生canvas沒有完備的事件系統，重繪機制繁瑣；

當然，現在也有很多優秀的canvas框架能夠解決上述問題，比如fabric.js和konva.js，尤其是fabric.js，讓我們使用canvas不再別扭，感興趣的同學也可以嘗試一下。

2.3 svg

svg是一種基于XML語法的圖像格式，是可縮放的矢量圖形。那什么是矢量圖形呢？矢量圖是計算機圖形學中用點、直線或者多邊形等基于數學方程的幾何圖元表示的圖像，所以矢量圖具有無論放大多少倍都不會失真的特性。而與之相對應的則是位圖，位圖是用像素陣列表示的圖像。svg在繪制圖表上有天然的優勢，

開發成本低svg基于XML語法，XML語法是一種類似于HTML語法的可擴展標記語言，也就是說svg是使用一系列的元素(line、circle，polygon等)來描述圖形的。那svg元素和dom元素之間是不是存在著某種關聯呢？

我們由元素間的繼承關系可以得出的結論是：svg元素和dom元素基本相似，因此對于svg元素，完全可以從dom元素的角度去理解和應用，上手成本幾乎就可以忽略不計了。并且svg和css，javascript等其他網絡標準無縫銜接。本質上，svg相對于圖像，就好比html相對于文本；
完備的事件系統由于svg元素與dom元素類似，因此dom元素中的事件系統對于svg同樣適用；
文件體積小，兼容性好前文已經介紹過，svg繪制出來的是一種矢量圖形，而矢量圖形都是使用點、直線等幾何圖元構成的圖形，是對圖像的圖形描述，本質上依然是文本文件，所以它具有體積小的天然優勢。svg是由萬維網聯盟（W3C）自1999年開始開發的開放標準。兼容性方面幾乎所有主流瀏覽器都支持。

因此，最終我選擇了使用svg來繪制圖表。

3、svg基礎

在我們正式繪制圖表之前，首先需要了解一些svg的基礎知識。

3.1 svg元素

svg圖像就是使用不同的svg元素來創建的，svg元素常用的主要分為動畫元素，形狀元素，字體元素，圖形元素，文本元素等。

形狀元素<circle>, <ellipse>, <line>, <mesh>, <path>, <polygon>, <polyline>, <rect>形狀元素是繪制svg圖像最常用的，path元素是svg中一個非常強大的元素，它類似于canvas中的path，利用它能夠繪制出任何你想要的圖形。在我們本次繪制圖表過程中，path元素亦不可或缺；
動畫元素<animate>，<animateColor>，<animateMotion>，<animateTransform>，<discard>，<mpath>，<set>想要給svg元素添加動畫，最簡單的方式是使用動畫元素，即用動畫元素包裹住svg圖形，即可添加動畫；

其他元素就不再贅述。

3.2 svg應用場景

iconfont圖標庫和字體庫iconfont圖標庫應該是svg最常見的一個使用場景，svg矢量圖、文件小的特性使得它非常適合來繪制小圖標，像我們轉轉的圖標庫也是使用svg來繪制的。svg繪制圖標也有一些小小的缺點，比如它只能繪制純色或者css漸變色圖標，從顏色方面來說沒有圖片色系豐富，層次分明。
業務動畫我們業務中一些常用的動畫場景也會使用svg實現，比如loading效果，圓環進度條，商品添加購物車特效等；像商品添加購物車的特效在電商網站是非常常見的，一般我們的實現思路是使用js+css動畫實現；其實svg中的路徑動畫更適用于這個場景，我們可以在需要加購的商品和購物車之間繪制一條隱形的path，當用戶觸發加購操作的時候觸發路徑動畫，即animateMotion，這樣也可以實現同樣的功能。

4、svg如何繪制圖表？

通過以上對背景以及一些前置知識的介紹，相信大家已經對svg有了一個初步的了解，接下來我們就回到最初的問題，如何通過svg來從頭開始繪制一個曲線面積圖？我主要分了以下幾個步驟，下文會對每個步驟逐一進行說明。

4.1 坐標系

計算機繪圖使用的坐標系統都是網格坐標系。其以左上角作為坐標系的原點，X軸正方形向右逐漸開始增大，Y軸正方向向下逐漸開始增大。

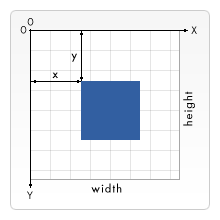
圖例來源于網絡

了解了svg的坐標系之后，我們來繪制曲線面積圖中的坐標系，坐標系其實就是由兩條線相交而成，svg中的line元素就是用來繪制直線的，所以使用line元素就可以繪制出X軸和Y軸。需要注意的是svg的坐標系原點在左上角，而我們需要實現的圖表中坐標系原點在左下角，所以在實現的時候要對y軸的實際坐標進行處理。

createCoordinate() {
      this.svg.createLine(
        [
          {
            x1: '0',
            y1: '0',
            x2: '0',
            // ui設計稿上y軸高度為205，由于頂部游標的存在（游標高度57，寬度122），所以y軸變為205+57；
            // 由于整個坐標軸往下平移了57，所以最下面的坐標會出現不顯示的情況，故再增加50的buffer
            y2: `${this.$toRealPx(262 + 50)}px`,
            stroke: '#F0F0F0',
            'stroke-width': '1',
          },
          {
            x1: '0',
            y1: `${this.$toRealPx(262 + 50)}px`,
            x2: `${this.$toRealPx(595)}px`,
            y2: `${this.$toRealPx(262 + 50)}px`,
            stroke: '#F0F0F0',
            'stroke-width': '1',
          },
        ],
        this.svgObj
      )
    }

4.2 網格

在我們需要實現的兩個圖表中，圖表背景處均有網格，網格的實現原理也是使用line元素，只要標記好起點以及終點，就可以完美繪制。此處不再展開。

4.3 數據點和數據游標

數據點：即用來標記當前數據位置的小原點，數據點有兩種狀態，分別是未點擊態和點擊態，實現數據點我們使用svg中的circle元素即可。當數據點被點擊時，我們只需要更改circle元素的填充屬性。

const circlePoints = this.graphAxisData.map((v, idx) => {
        return {
          cx: v.xAxis,
          cy: v.yAxis || 0,
          r: this.$toRealPx(5),
          stroke: '#7792D8',
          'stroke-width': this.$toRealPx(3),
          fill: 'white',
          title: `class${idx + 1}`,
          imageIndex: `imageClass${idx + 1}`,
        }
      })

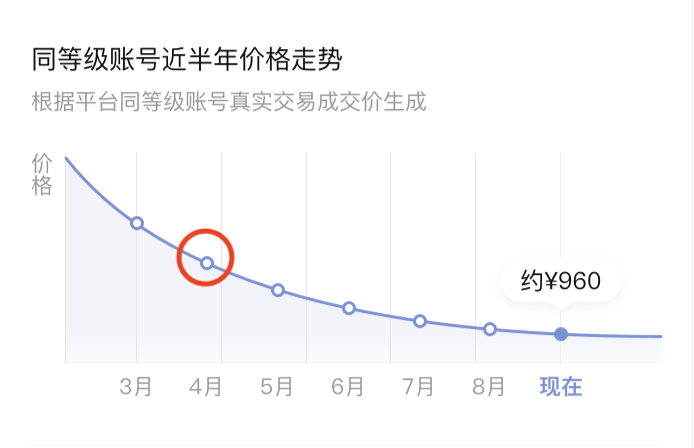
數據游標：數據游標在我們的圖表里是一個不規則圖形，其有點類似于會話氣泡。我們要實現數據游標有兩種方式，第一種方式是使用svg的path元素來繪制，那path元素的參數具體應該怎么設置呢？其實可以跟設計師同學溝通，一般設計同學在用設計軟件導出的時候，設計軟件會攜帶path元素的具體參數，這是方案一；還有第二種比較簡單的方案是利用svg中的image元素，也就是將數據游標當作一個圖片繪制到圖表中，這種方案比較簡單省事，我采用的也是此方案。

const circleImage = this.graphAxisData.map((v, idx) => {
        return {
          x: (v.xAxis - this.$toRealPx(122) / 2),
          y: (v.yAxis - this.$toRealPx(52) - this.$toRealPx(8)) || 0,
          height: this.$toRealPx(52),
          width: this.$toRealPx(122),
          id: `imageClass${idx + 1}`,
          href: 'https://pic3.zhuanstatic.com/zhuanzh/b13744dd-c240-4961-8054-9f923586ea5a.png',
        }
      })
      const circleText = this.graphAxisData.map((v, idx) => {
        return {
          x: v.xAxis,
          y: (v.yAxis - this.$toRealPx(52 / 2)) || 0,
          fill: '#111111',
          'font-size': this.$toRealPx(24),
          'text-anchor': 'middle',
          title: `￥${v.oriYAxis}`,
          id: `class${idx + 1}`,
        }
      })

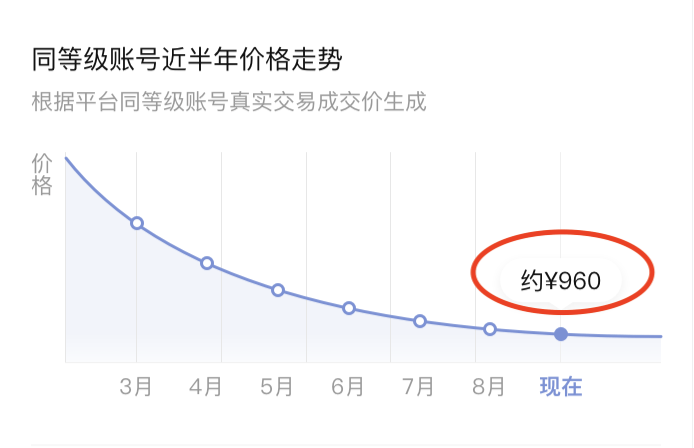
4.4 曲線

接下來就要繪制圖表中最重要的一個部分，也就是用真實數據渲染出來的一條曲線，繪制曲線我們依然是利用path元素繪制貝塞爾曲線，貝塞爾曲線只需要少量的點就可以繪制一條光滑曲線。在svg中，path元素用來繪制貝塞爾曲線的命令有兩組，第一組是C,S命令，用來繪制三次貝塞爾曲線；第二組是Q,T命令，用來繪制二次貝塞爾曲線。

我繪制圖表使用的是三次貝塞爾曲線，那首先了解一下三次貝塞爾曲線。

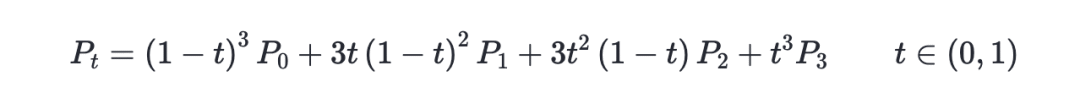
其中，t代表斜率，取值為0-1;p0代表起始點坐標(x0,y0);p1代表第一個控制點坐標(x1,y1);p2代表第二個控制點坐標(x2,y2);p3代表終點坐標(x3,y3);pt代表這條曲線上的任意一個點坐標(xt,yt)。當t由0-1逐漸變化的時候，可以得到一系列的(xt,yt),這一系列(xt,yt)就組成了一條三次貝塞爾曲線，這就是三次貝塞爾曲線的定義。

通過以上介紹可知，繪制三次貝塞爾曲線必須得知道起始點、兩個控制點以及終點。后端會返回給我們相應的幾個數據點，也就是說這幾個數據點的坐標是已知的，現在的問題就成了給定一組已知數據點，如何擬合成一條曲線？其實思路很簡單，假如說有已知的5個點，那么我們將第一個點作為起始點，第二個點作為終點，計算出他們之間的控制點，繪制一條曲線，同樣的，又以第二個點作為起點，第三個點作為終點，再重復以上過程，最終即繪制出一條橫穿五個點的平滑曲線。

此處附上算法源碼

createBezierLine() {
      const polygonPath = this.getCubicBezierCurvePath(
        this.graphAxisData.map((v) => {
          return {
            x: v.xAxis,
            y: v.yAxis,
          }
        })
      )

      this.svg.createPath(
        {
          d: polygonPath,
          fill: 'none',
          stroke: '#7792D8',
          'stroke-width': 2
        },
        this.svgObject
      )
    }
    
getCubicBezierCurvePath(knots) {
      const firstControlPoints = []
      const secondControlPoints = []
      const path = []

      this.getCubicBezierCurvePoints(knots, firstControlPoints, secondControlPoints)

      for (let i = 0, len = knots.length; i < len; i++) {
        if (i === 0) {
          path.push(['M', knots[i].x, knots[i].y].join(' '))
        } else {
          const firstControlPoint = firstControlPoints[i - 1]
          const secondControlPoint = secondControlPoints[i - 1]
          path.push(
            [
              'C',
              firstControlPoint.x,
              firstControlPoint.y, // 第一個控制點
              secondControlPoint.x,
              secondControlPoint.y, // 第二個控制點
              knots[i].x,
              knots[i].y, // 實點
            ].join(' ')
          )
        }
      }

      return path.join(' ')
    }
    
getCubicBezierCurvePoints(knots, firstControlPoints, secondControlPoints) {
      const rhs = []
      const n = knots.length - 1
      let x = 0
      let y = 0
      let i = 0

      if (n < 1) {
        return
      }

      // Set right hand side X values0
      for (i = 0; i < n - 1; ++i) {
        rhs[i] = 4 * knots[i].x + 2 * knots[i + 1].x
      }
      rhs[0] = knots[0].x + 2 * knots[1].x
      rhs[n - 1] = 3 * knots[n - 1].x

      // Get first control points X-values
      x = this.getFirstControlPoints(rhs)

      // Set right hand side Y values
      for (i = 1; i < n - 1; ++i) {
        rhs[i] = 4 * knots[i].y + 2 * knots[i + 1].y
      }
      rhs[0] = knots[0].y + 2 * knots[1].y
      rhs[n - 1] = 3 * knots[n - 1].y

      // Get first control points Y-values
      y = this.getFirstControlPoints(rhs)

      for (i = 0; i < n; ++i) {
        // First control point
        firstControlPoints[i] = {
          x: x[i],
          y: y[i],
        }

        // Second control point
        if (i < n - 1) {
          secondControlPoints[i] = {
            x: 2 * knots[i + 1].x - x[i + 1],
            y: 2 * knots[i + 1].y - y[i + 1],
          }
        } else {
          secondControlPoints[i] = {
            x: (knots[n].x + x[n - 1]) / 2,
            y: (knots[n].y + y[n - 1]) / 2,
          }
        }
      }
    }
    
getFirstControlPoints(rhs) {
      const n = rhs.length
      const x = [] // Solution vector.
      const tmp = [] // Temp workspace.
      let b = 2.0
      let i = 0
      x[0] = rhs[0] / b

      for (i = 1; i < n; i++) {
        // Decomposition and forward substitution.
        tmp[i] = 1 / b
        b = (i < n - 1 ? 4.0 : 2.0) - tmp[i]
        x[i] = (rhs[i] - x[i - 1]) / b
      }

      for (i = 1; i < n; i++) {
        x[n - i - 1] -= tmp[n - i] * x[n - i] // Backsubstitution.
      }
      return x
    }

4.5 面積

最后一步就是繪制曲線與X軸和Y軸相交而形成的面積部分。假如說這條曲線不是一條曲線而是一條折線的話，那么其實很容易就能實現。我們將這條折線與X軸和Y軸連接起來形成一個閉合圖形polygon，然后通過給polygon進行填充即可得到折線的面積圖。

我們利用這個思路，如果一條折線上的點足夠多的話，那么這條折線就會無限趨近于一條曲線。反之，一條曲線也可以看成是無限多的點構成的折線，所以我們利用svg中的getTotalLength()和getPointAtLength()這兩個方法就可以將path轉換為多邊形，最后再填充多邊形即可得到最終的面積圖。

5、結語

通過以上5個步驟，我們就能夠基于svg從頭開始實現一個簡單的曲線面積圖。svg的使用場景還是非常豐富的，并且兼容性一直都不錯，如果需要實現這種相對不那么復雜且交互少的圖形，svg還是一個不錯的方案。如果要實現復雜圖層、復雜動效以及復雜交互，canvas框架可能會是一個更好的選擇。

最后，開年第一篇，祝大家新年快樂，2023突（兔）飛猛進，大展鴻圖（兔），前途（兔）無量！

參考

??https://www.infoq.cn/article/ogwddr4u8x0s*5aaytsh??? ??https://gist.github.com/mingzhi22/be3324ffd9765687ea2f??

責任編輯：武曉燕來源：大轉轉FE

圖表指南圖形化

成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看