Stackoverflow：計算兩個整數的最小公倍數的最有效方法是什么？

作者：小傅哥 2023-01-11 08:51:34

開發前端

短除法能解決計算最大公約數的問題，但放到程序編寫中總是很別扭，總不能一個個數字去試算，這就顯得很鬧挺。其實除了短除法還有一種是計算公約數的辦法，叫做歐幾里德算法。

一、前言

嘿，小傅哥怎么突然講到最大公約數了？

這么想你肯定是沒有好好閱讀前面章節中小傅哥講到的RSA算法，對于與歐拉結果計算的互為質數的公鑰e，其實就需要使用到輾轉相除法來計算出最大公約數。

放心，你所有寫的代碼，都是對數學邏輯的具體實現，無非是難易不同罷了。所以如果你真的想學好編程思維而不只是CRUD，那就要把數據結構、算法邏輯等根基打牢。

二、短除法

既然都說到這了，那你還記得怎么計算最大公約數嗎，死鬼？

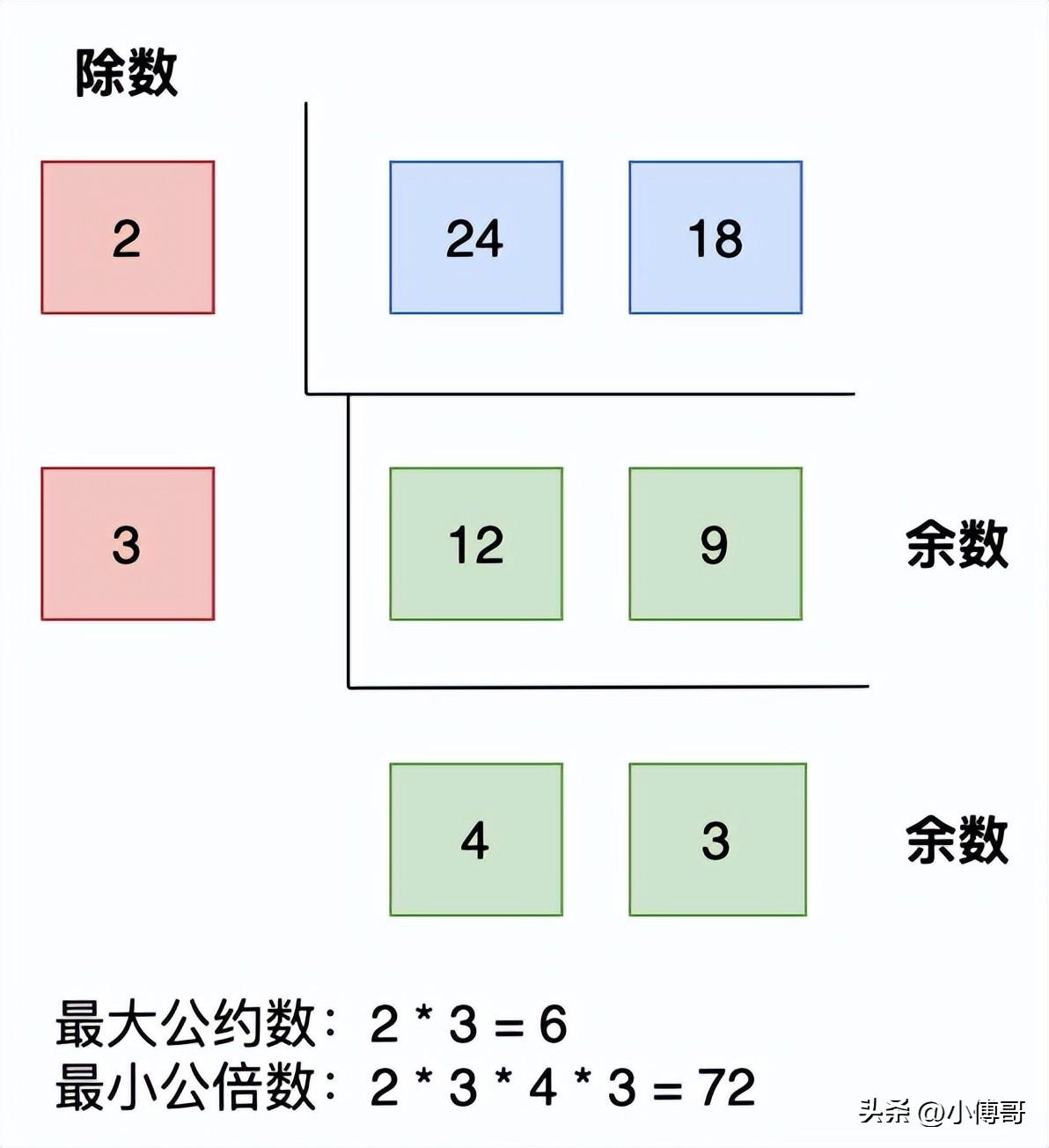
以上這種方式就是我們在上學階段學習的，這種計算方式叫做短除法。

短除法：是算術中除法的算法，將除法轉換成一連串的運算。短除法是由長除法簡化而來，當中會用到心算，因此除數較小的除法比較適用短除法。對大部分的人而言，若除以12或12以下的數，可以用記憶中乘法表的內容，用心算來進行短除法。也有些人可以處理除數更大的短除法。—— 來自維基百科

三、歐幾里德算法

歐幾里德算法：是計算兩個整數（數字）的最大公約數【GCD(Greatest Common Divisor)】的有效方法，即能將它們整除而無余數的最大數。它以古希臘數學家歐幾里得的名字命名，歐幾里德在他的幾何原本（約公元前 300 年）中首次描述了它。它是算法的示例，是根據明確定義的規則執行計算的分步過程，并且是常用的最古老的算法之一。它可以用來減少分數到他們的最簡單的形式，并且是許多其他數論和密碼計算的一部分。—— 來自維基百科

GCD，代表了兩個數字的最大公約數，GCD(X,Y) = Z，那么就表示 X 和 Y 的最大公約數是 Z。由歐幾里德算法給出 GCD(X,Y) = GCD(Y,XmodY) —— mod 表示求模計算余數。

其實簡單來說就是，X和Y的公約數是Z，那么Y和Z的公約數也是Z。24和18的最大公約數是6，那么18和6的公約數也是6。嘿，就這么一個事。但就因為有了這一樣一條推論，讓編程代碼變得優雅舒服，只需要不斷地將X、Y兩數作差，就能計算最大公約數。

這讓小傅哥想起，多年前上學時候，我也給出過一條推論；”任意一組所能構成等差數列的三個數字，所能組合出來的一個三位數，都能被3整除。“ 例如：等差數列 16、31、46 組合成三位數 463116 或者 461631 都能被3整除。

四、輾轉相除法代碼實現

歐幾里德算法 = 輾轉相除法法：https://en.wikipedia.org/wiki/Euclidean_algorithm

在輾轉相除法的實現中，計算最大公約數的方式，就是使用一個數字減去另外一個數字，直到兩個數字相同或者有其中一個數字為0，那么最后不為零的那個數字就是兩數的最大公約數。

小傅哥在這里提供了2種計算方式，一種是循環另外一種是遞歸。—— 方便很多看不懂遞歸的小伙伴可以用另外的方式學習。

1. 循環實現

public long gcd01(long m, long n){
    m = Math.abs(m);
    n = Math.abs(n);
    
    while (m != 0 && n != 0 && m != n) {
        if (m > n) {
            m = m - n;
        } else {
            n = n - m;
        }
    }
    return m == 0 ? n : m;
}

兩數循環處理中，條件為 m != 0 && n != 0 && m != n直至循環結束。

2. 遞歸實現

public long gcd02(long m, long n){
    if (m < n) {
        long k = m;
        m = n;
        n = k;
    }
    if (m % n != 0) {
        long temp = m % n;
        return gcd02(n, temp);
    } else {
        return n;
    }
}

計算方式邏輯和條件是一樣的，只不過這個是使用了遞歸調用的方式進行處理。

3. 測試驗證

@Test
public void test_euclidean() {
    Euclidean euclidean = new Euclidean();
    System.out.println(euclidean.gcd01(124, 20));
    System.out.println(euclidean.gcd02(124, 20));
}

測試結果

4
4


Process finished with exit code 0

計算 124 和 20 的最大公約數，兩個計算方式結果都是 4 。好的，到這測試通過。
這并不是一個很難的知識點，但當你做一些技術分享、答辯述職等時候，能這樣用技術語言而不是大白話的講述出來后，其實高度就有了。兄弟！

在 stackoverflow.com 看到一道問題：計算兩個整數的最小公倍數的最有效方法是什么？

乍一看，這能有啥。不就是計算下最小公倍數嗎？但一想我腦袋中計算最小公倍數的方法；一種是在本子上通過短除法計算，另外一種是基于計算出的最大公約數，再使用公式：lcm(a, b) = |a * b| / gcd(a, b) 求得最小公倍數。—— 計算最大公約數是基于歐幾里德算法(輾轉相除法)

那么這樣的計算方法是不是最有效的方法，另外如果是同時計算多個整數的最小公倍數，要怎么處理？

其實編程的學習往往就是這樣，留心處處都是學問，你總是需要從各種細小的點中，積累自己的技術思維廣度和縱向探索深度。好啦，接下來小傅哥就給大家介紹幾種用于計算最小公倍數的算法。

五、用公約數實現

公式：lcm(a, b) = |a * b| / gcd(a, b)

public long lcm01(long m, long n){
    return ((m == 0) || (n == 0)) ? 0 : Math.abs(m * n) / gcd(m, n);
}

private long gcd(long m, long n){
    m = Math.abs(m);
    n = Math.abs(n);
    // 從一個數字中減去另一個數字，直到兩個數字變得相同。
    // 這將是 GCD。如果其中一個數字為零，也退出循環。
    // https://en.wikipedia.org/wiki/Euclidean_algorithm
    while (m != 0 && n != 0 && m != n) {
        if (m > n) {
            m = m - n;
        } else {
            n = n - m;
        }
    }
    return m == 0 ? n : m;
}

首先這里是一個比較簡單的方式，基于兩數乘積除以最大公約數，得到的結果就是最小公倍數。

六、簡單累加計算

此計算方式為，在一組正整數數列中，通過找到最小的數字進行自身累加循環，直至所有數字相同時，則這個數字為最小公倍數。—— 你能代碼實現一下嗎？

public long lcm02(long... n) {
    long[] cache = n.clone();
    // 以所有數字都相等作為條件
    while (!isEquals(n)) {
        System.out.println(JSON.toJSONString(n));
        long min = n[0];
        int idx = 0;
        for (int i = 0; i < n.length; i++) {
            if (min > n[i]) {
                min = n[i];
                idx = i;
            }
        }
        n[idx] = cache[idx] + min;
    }
    return n[0];
}

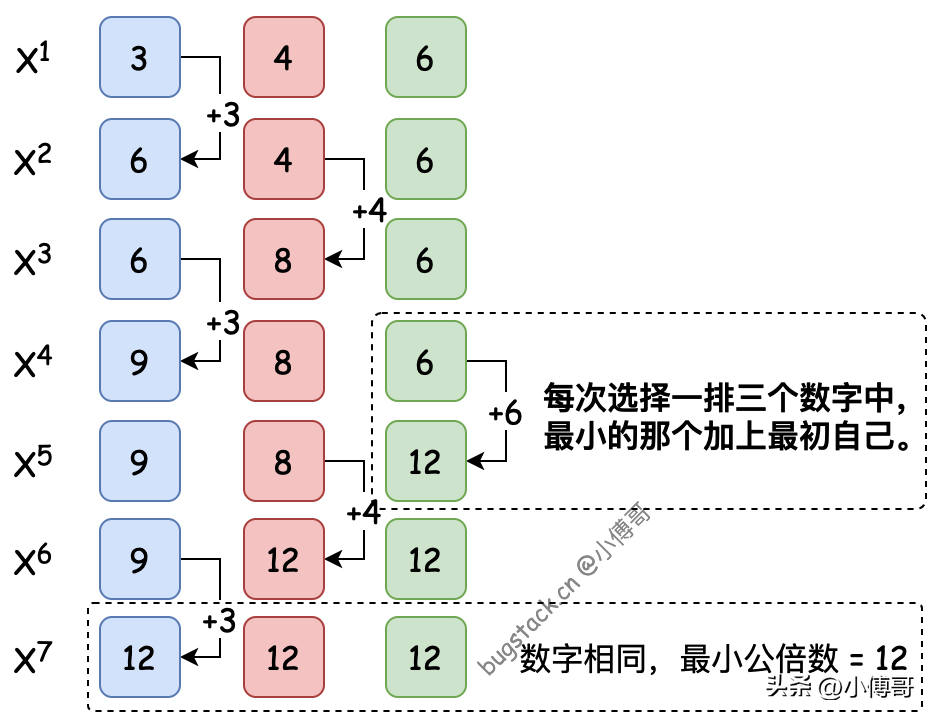
在代碼實現中，首先要把n個整數數列進行克隆保存。因為每次相加的都是最初的這個數列里的數字值。接下來就是以所有數字都相等作為條件循環判斷，不斷地的累加最小的數值即可。最終返回的就是最小公倍數。

七、表格推演計算

表格計算方式為將一組數字以最小的質數2開始整除，直到不能被2整除后，用下一個質數3繼續整除（剩余的數字中比大的最小的質數）直至所有數字都為1的時候結束。最終所有有效的質數乘積就是最小公倍數。—— 想想如果這讓你用代碼實現，你能肝出來嗎？

public long lcm03(long... n) {
    Map<Long, List<Long>> keys = new HashMap<>();
    for (long key : n) {
        keys.put(key, new ArrayList<Long>() {{
            add(key);
        }});
    }
    System.out.print("執行表格計算：\r\nx ");
    long primality = 2, cachePrimality = primality, filterCount = 0, lcm = 1;
    // 以所有元素最后一位為1作為條件
    while (filterCount != keys.size()) {
        int refresh = 0;
        filterCount = 0;
        for (Map.Entry<Long, List<Long>> entry : keys.entrySet()) {
            long value = entry.getValue().get(entry.getValue().size() - 1);
            if (value == 1) {
                filterCount++;
            }
            // 整除處理
            if (value % primality == 0) {
                entry.getValue().add(value / primality);
                refresh++;
            } else {
                entry.getValue().add(value);
            }
        }
        // 刷新除數
        if (refresh == 0) {
            for (Map.Entry<Long, List<Long>> entry : keys.entrySet()) {
                long value = entry.getValue().get(entry.getValue().size() - 1);
                // 找到下一個符合的素數
                if (value > primality || (value < cachePrimality && value > primality)) {
                    cachePrimality = value;
                }
                entry.getValue().remove(entry.getValue().size() - 1);
            }
            primality = cachePrimality;
        } else {
            // 累計乘積
            lcm *= cachePrimality;
            System.out.print(cachePrimality + " ");
        }
    }
    keys.forEach((key, values) -> {
        System.out.println();
        for (long v : values) {
            System.out.print(v + " ");
        }
    });
    System.out.println("\r\n");
    return lcm;
}

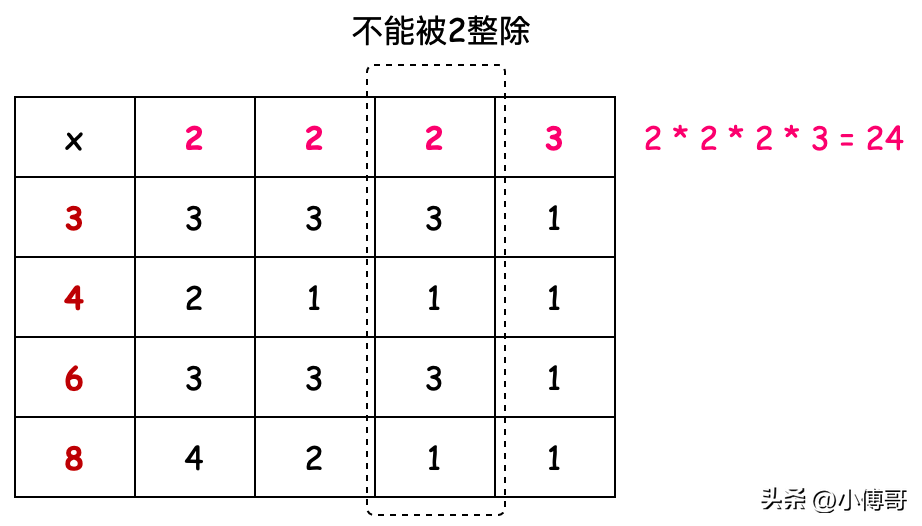
在代碼實現中我們通過 Map 作為表的key，Map 中的 List 作為表每一行數據。通過這樣一個結構構建出一張表。
接下來以所有元素最后一位為1作為條件循環處理數據，用最開始的2作為素數整除列表中的數據，并保存到下一組數列中。當2不能整除時，則刷新素數，選取另外一個列表中最小的素數作為除數繼續。
這個過程中會累計有效素數的乘積，這個乘積的最終結果就是最小公倍數。

八、測試驗證

單元測試

@Test
public void test_euclidean() {
    LastCommonMultiple lastCommonMultiple = new LastCommonMultiple();
    // System.out.println("最小公倍數：" + lastCommonMultiple.lcm01(2, 7));
    System.out.println("最小公倍數：" + lastCommonMultiple.lcm02(3, 4, 6));
    // System.out.println("最小公倍數：" + lastCommonMultiple.lcm03(3, 4, 6));
     System.out.println("最小公倍數：" + lastCommonMultiple.lcm03(3, 4, 6, 8));
   //System.out.println("最小公倍數：" + lastCommonMultiple.lcm03(4, 7, 12, 21, 42));
}

測試結果

執行累加計算：
[3,4,6]
[6,4,6]
[6,8,6]
[9,8,6]
[9,8,12]
[9,12,12]
最小公倍數：12

執行表格計算：
x 2 2 2 3 
3 3 3 3 1 
4 2 1 1 1 
6 3 3 3 1 
8 4 2 1 1 

最小公倍數：24

到這里測試就結束了，本章一共介紹了三種計算最小公倍數的方法。那如果只讓你看到邏輯，你能寫出最終的代碼嗎？

九、常見面試

最大公約數的使用用途？
如何使用代碼實現最大公約數計算？
你是否了解歐幾里德算法？
關于數論你還記得多少？
RSA 加密算法為什么需要用到公約數計算？
如何計算兩數的最小公倍數？
如果計算多個整數的最小公倍數？
你能說一下具體如何實現這種X的計算流程嗎？
你知道最小公倍數計算的用途嗎？

What is the most efficient way to calculate the least common multiple of two integers?：https://stackoverflow.com/questions/3154454/what-is-the-most-efficient-way-to-calculate-the-least-common-multiple-of-two-int/3154503#3154503
Least common multiple：https://en.wikipedia.org/wiki/Least_common_multiple
Chebyshev function：https://en.wikipedia.org/wiki/Chebyshev_function
歐幾里德算法：https://en.wikipedia.org/wiki/Euclidean_algorithm
線性組合：https://en.wikipedia.org/wiki/Linear_combination
貝祖定理：https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity?

責任編輯：武曉燕來源：今日頭條

最大公約數公約數試算

成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看

Stackoverflow：計算兩個整數的最小公倍數的最有效方法是什么？

一、前言

二、短除法

三、歐幾里德算法

四、輾轉相除法代碼實現

1. 循環實現

2. 遞歸實現

3. 測試驗證

五、用公約數實現

六、簡單累加計算

七、表格推演計算

八、測試驗證

單元測試

測試結果

九、常見面試