本文將比較各種降維技術在機器學習任務中對表格數據的有效性。我們將降維方法應用于數據集,并通過回歸和分類分析評估其有效性。我們將降維方法應用于從與不同領域相關的 UCI 中獲取的各種數據集。總共選擇了 15 個數據集,其中 7 個將用于回歸,8 個用于分類。
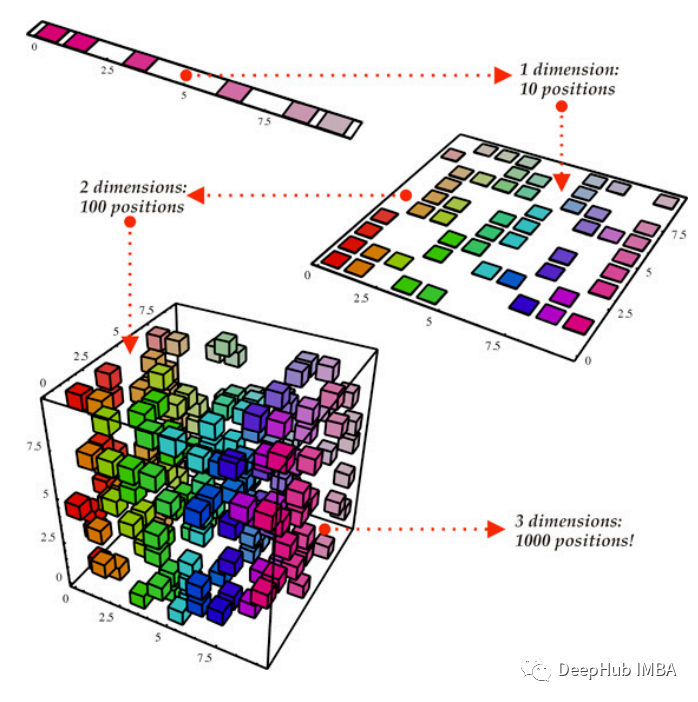
為了使本文易于閱讀和理解,僅顯示了一個數據集的預處理和分析。實驗從加載數據集開始。數據集被分成訓練集和測試集,然后在均值為 0 且標準差為 1 的情況下進行標準化。
然后會將降維技術應用于訓練數據,并使用相同的參數對測試集進行變換以進行降維。對于回歸,使用主成分分析(PCA)和奇異值分解(SVD)進行降維,另一方面對于分類,使用線性判別分析(LDA)
降維后就訓練多個機器學習模型進行測試,并比較了不同模型在通過不同降維方法獲得的不同數據集上的性能。
數據處理讓我們通過加載第一個數據集開始這個過程,
import pandas as pd ## for data manipulation
df = pd.read_excel(r'Regression\AirQualityUCI.xlsx')
print(df.shape)
df.head()

數據集包含15個列,其中一個是需要預測標簽。在繼續降維之前,日期和時間列也會被刪除。
X = df.drop(['CO(GT)', 'Date', 'Time'], axis=1)
y = df['CO(GT)']
X.shape, y.shape
#Output: ((9357, 12), (9357,))
為了訓練,我們需要將數據集劃分為訓練集和測試集,這樣可以評估降維方法和在降維特征空間上訓練的機器學習模型的有效性。模型將使用訓練集進行訓練,性能將使用測試集進行評估。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
#Output: ((7485, 12), (1872, 12), (7485,), (1872,))
在對數據集使用降維技術之前,可以對輸入數據進行縮放,這樣可以保證所有特征處于相同的比例上。這對于線性模型來說是是至關重要的,因為某些降維方法可以根據數據是否標準化以及對特征的大小敏感而改變其輸出。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
X_train.shape, X_test.shape
主成分分析(PCA)
線性降維的PCA方法降低了數據的維數,同時保留了盡可能多的數據方差。
這里將使用Python sklearn.decomposition模塊的PCA方法。要保留的組件數量是通過這個參數指定的,這個數字會影響在較小的特征空間中包含多少維度。作為一種替代方法,我們可以設定要保留的目標方差,它根據捕獲的數據中的方差量建立組件的數量,我們這里設置為0.95
from sklearn.decomposition import PCA
pca = PCA(n_compnotallow=0.95)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)
X_train_pca

上述特征代表什么?主成分分析(PCA)將數據投射到低維空間,試圖盡可能多地保留數據中的不同之處。雖然這可能有助于特定的操作,但也可能使數據更難以理解。,PCA可以識別數據中的新軸,這些軸是初始特征的線性融合。
奇異值分解(SVD)
SVD是一種線性降維技術,它將數據方差較小的特征投影到低維空間。我們需要設置降維后要保留的組件數量。這里我們將把維度降低 2/3。
from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_compnotallow=int(X_train.shape[1]*0.33))
X_train_svd = svd.fit_transform(X_train)
X_test_svd = svd.transform(X_test)
X_train_svd

訓練回歸模型
現在,我們將開始使用上述三種數據(原始數據集、PCA和SVD)對模型進行訓練和測試,并且我們使用多個模型進行對比。
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.metrics import r2_score, mean_squared_error
import time
train_test_ML:這個函數將完成與模型的訓練和測試相關的重復任務。通過計算rmse和r2_score來評估所有模型的性能。并返回包含所有詳細信息和計算值的數據集,還將記錄每個模型在各自的數據集上訓練和測試所花費的時間。
def train_test_ML(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'R2 Score', 'RMSE', 'Time Taken'])
for i in [LinearRegression, KNeighborsRegressor, SVR, DecisionTreeRegressor, RandomForestRegressor, GradientBoostingRegressor]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
r2 = np.round(r2_score(y_test, y_pred), 2)
rmse = np.round(np.sqrt(mean_squared_error(y_test, y_pred)), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], r2, rmse, time_taken]
return temp_df
原始數據:
original_df = train_test_ML('AirQualityUCI', 'Original', X_train, y_train, X_test, y_test)
original_df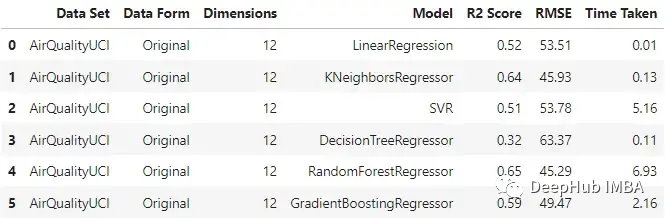
可以看到KNN回歸器和隨機森林在輸入原始數據時表現相對較好,隨機森林的訓練時間是最長的。
PCA
pca_df = train_test_ML('AirQualityUCI', 'PCA Reduced', X_train_pca, y_train, X_test_pca, y_test)
pca_df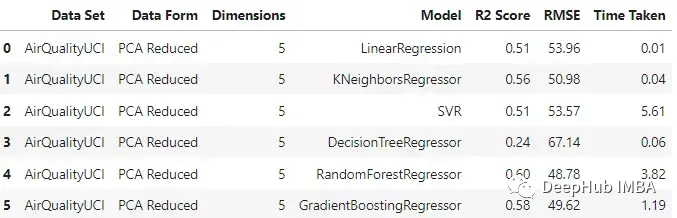
與原始數據集相比,不同模型的性能有不同程度的下降。梯度增強回歸和支持向量回歸在兩種情況下保持了一致性。這里一個主要的差異也是預期的是模型訓練所花費的時間。與其他模型不同的是,SVR在這兩種情況下花費的時間差不多。
SVD
svd_df = train_test_ML('AirQualityUCI', 'SVD Reduced', X_train_svd, y_train, X_test_svd, y_test)
svd_df
與PCA相比,SVD以更大的比例降低了維度,隨機森林和梯度增強回歸器的表現相對優于其他模型。
回歸模型分析
對于這個數據集,使用主成分分析時,數據維數從12維降至5維,使用奇異值分析時,數據降至3維。
- 就機器學習性能而言,數據集的原始形式相對更好。造成這種情況的一個潛在原因可能是,當我們使用這種技術降低維數時,在這個過程中會發生信息損失。
- 但是線性回歸、支持向量回歸和梯度增強回歸在原始和PCA案例中的表現是一致的。
- 在我們通過SVD得到的數據上,所有模型的性能都下降了。
- 在降維情況下,由于特征變量的維數較低,模型所花費的時間減少了。
將類似的過程應用于其他六個數據集進行測試,得到以下結果:
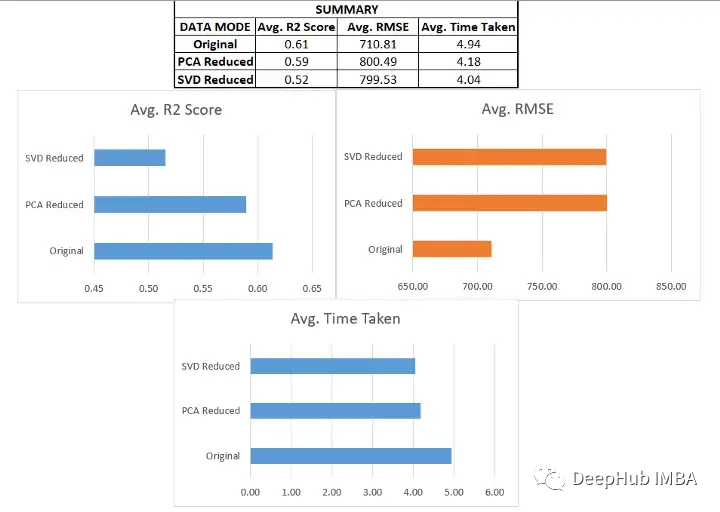
我們在各種數據集上使用了SVD和PCA,并對比了在原始高維特征空間上訓練的回歸模型與在約簡特征空間上訓練的模型的有效性
- 原始數據集始終優于由降維方法創建的低維數據。這說明在降維過程中可能丟失了一些信息。
- 當用于更大的數據集時,降維方法有助于顯著減少數據集中的特征數量,從而提高機器學習模型的有效性。對于較小的數據集,改影響并不顯著。
- 模型的性能在original和pca_reduced兩種模式下保持一致。如果一個模型在原始數據集上表現得更好,那么它在PCA模式下也會表現得更好。同樣,較差的模型也沒有得到改進。
- 在SVD的情況下,模型的性能下降比較明顯。這可能是n_components數量選擇的問題,因為太小數量肯定會丟失數據。
- 決策樹在SVD數據集時一直是非常差的,因為它本來就是一個弱學習器
訓練分類模型
對于分類我們將使用另一種降維方法:LDA。機器學習和模式識別任務經常使用被稱為線性判別分析(LDA)的降維方法。這種監督學習技術旨在最大化幾個類或類別之間的距離,同時將數據投影到低維空間。由于它的作用是最大化類之間的差異,因此只能用于分類任務。
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import accuracy_score, f1_score, recall_score, precision_score
繼續我們的訓練方法
def train_test_ML2(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'Accuracy', 'F1 Score', 'Recall', 'Precision', 'Time Taken'])
for i in [LogisticRegression, KNeighborsClassifier, SVC, DecisionTreeClassifier, RandomForestClassifier, GradientBoostingClassifier]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
accuracy = np.round(accuracy_score(y_test, y_pred), 2)
f1 = np.round(f1_score(y_test, y_pred, average='weighted'), 2)
recall = np.round(recall_score(y_test, y_pred, average='weighted'), 2)
precision = np.round(precision_score(y_test, y_pred, average='weighted'), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], accuracy, f1, recall, precision, time_taken]
return temp_df
開始訓練
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis()
X_train_lda = lda.fit_transform(X_train, y_train)
X_test_lda = lda.transform(X_test)
預處理、分割和數據集的縮放,都與回歸部分相同。在對8個不同的數據集進行新聯后我們得到了下面結果:
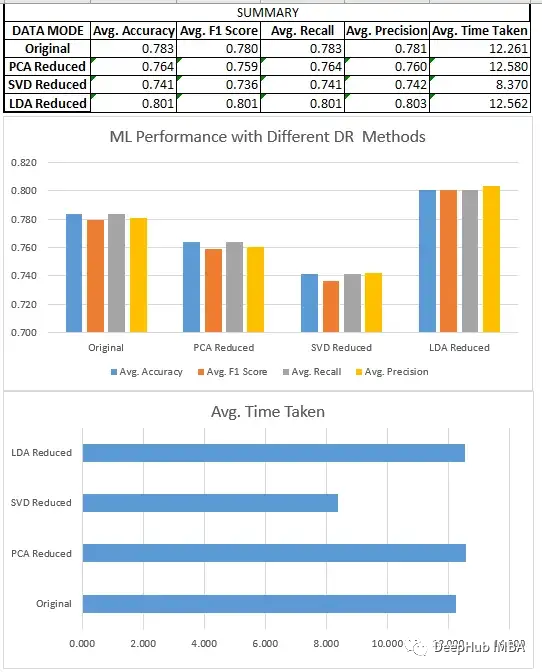
分類模型分析
我們比較了上面所有的三種方法SVD、LDA和PCA。
- LDA數據集通常優于原始形式的數據和由其他降維方法創建的低維數據,因為它旨在識別最有效區分類的特征的線性組合,而原始數據和其他無監督降維技術不關心數據集的標簽。
- 降維技術在應用于更大的數據集時,可以極大地減少了數據集中的特征數量,這提高了機器學習模型的效率。在較小的數據集上,影響不是特別明顯。除了LDA(它在這些情況下也很有效),因為它們在一些情況下,如二元分類,可以將數據集的維度減少到只有一個。
- 當我們在尋找一定的性能時,LDA可以是分類問題的一個非常好的起點。
- SVD與回歸一樣,模型的性能下降很明顯。需要調整n_components的選擇。
總結
我們比較了一些降維技術的性能,如奇異值分解(SVD)、主成分分析(PCA)和線性判別分析(LDA)。我們的研究結果表明,方法的選擇取決于特定的數據集和手頭的任務。
對于回歸任務,我們發現PCA通常比SVD表現得更好。在分類的情況下,LDA優于SVD和PCA,以及原始數據集。線性判別分析(LDA)在分類任務中始終擊敗主成分分析(PCA)的這個是很重要的,但這并不意味著LDA在一般情況下是一種更好的技術。這是因為LDA是一種監督學習算法,它依賴于有標簽的數據來定位數據中最具鑒別性的特征,而PCA是一種無監督技術,它不需要有標簽的數據,并尋求在數據中保持盡可能多的方差。因此,PCA可能更適合于無監督的任務或可解釋性至關重要的情況,而LDA可能更適合涉及標記數據的任務。
雖然降維技術可以幫助減少數據集中的特征數量,并提高機器學習模型的效率,但重要的是要考慮對模型性能和結果可解釋性的潛在影響。
本文完整代碼:
https://github.com/salmankhi/DimensionalityReduction/blob/main/Notebook_25373.ipynb